备考2023年中考数学压轴题训练 ——二次函数(5)
试卷更新日期:2023-05-14 类型:三轮冲刺
一、真题
-
1. 抛物线y=x2-4x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.
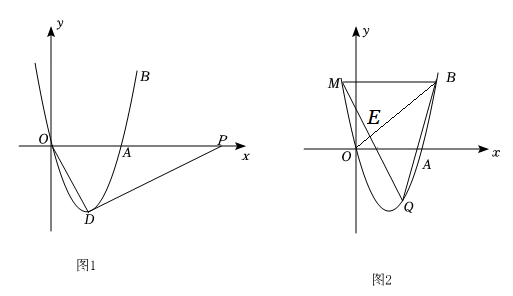 (1)、直接写出点B和点D的坐标;(2)、如图1,连接OD,P为x轴上的动点,当tan∠PDO=时,求点P的坐标;(3)、如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2 , 求的最大值.2. 已知抛物线 与 轴交于 , 两点,与 轴交于点 .直线 由直线 平移得到,与 轴交于点 .四边形 的四个顶点的坐标分别为 , , , .
(1)、直接写出点B和点D的坐标;(2)、如图1,连接OD,P为x轴上的动点,当tan∠PDO=时,求点P的坐标;(3)、如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2 , 求的最大值.2. 已知抛物线 与 轴交于 , 两点,与 轴交于点 .直线 由直线 平移得到,与 轴交于点 .四边形 的四个顶点的坐标分别为 , , , .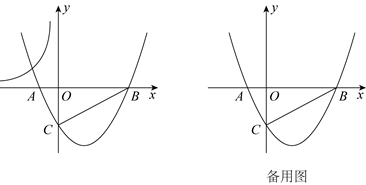 (1)、填空: , ;(2)、若点 在第二象限,直线 与经过点 的双曲线 有且只有一个交点,求 的最大值;(3)、当直线 与四边形 、抛物线 都有交点时,存在直线 ,对于同一条直线 上的交点,直线 与四边形 的交点的纵坐标都不大于它与抛物线 的交点的纵坐标.
(1)、填空: , ;(2)、若点 在第二象限,直线 与经过点 的双曲线 有且只有一个交点,求 的最大值;(3)、当直线 与四边形 、抛物线 都有交点时,存在直线 ,对于同一条直线 上的交点,直线 与四边形 的交点的纵坐标都不大于它与抛物线 的交点的纵坐标.①当 时,直接写出 的取值范围;
②求 的取值范围.
3. 抛物线与直线交于原点和点 , 与轴交于另一点 , 顶点为. (1)、直接写出点和点的坐标;(2)、如图1,连接 , 为轴上的动点,当时,求点的坐标;(3)、如图2,是点关于抛物线对称轴的对称点,是抛物线上的动点,它的横坐标为 , 连接 , , 与直线交于点设和的面积分别为和 , 求的最大值.4. 抛物线交轴于 , 两点(在的左边),是第一象限抛物线上一点,直线交轴于点.
(1)、直接写出点和点的坐标;(2)、如图1,连接 , 为轴上的动点,当时,求点的坐标;(3)、如图2,是点关于抛物线对称轴的对称点,是抛物线上的动点,它的横坐标为 , 连接 , , 与直线交于点设和的面积分别为和 , 求的最大值.4. 抛物线交轴于 , 两点(在的左边),是第一象限抛物线上一点,直线交轴于点.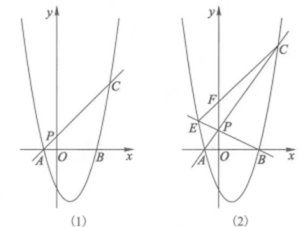 (1)、直接写出 , 两点的坐标;(2)、如图(1),当时,在抛物线上存在点(异于点),使 , 两点到的距离相等,求出所有满足条件的点的横坐标;(3)、如图(2),直线交抛物线于另一点 , 连接交轴于点 , 点的横坐标为.求的值(用含的式子表示).5. 已知抛物线 与 轴交于点 和点 两点,与 轴交于点 .
(1)、直接写出 , 两点的坐标;(2)、如图(1),当时,在抛物线上存在点(异于点),使 , 两点到的距离相等,求出所有满足条件的点的横坐标;(3)、如图(2),直线交抛物线于另一点 , 连接交轴于点 , 点的横坐标为.求的值(用含的式子表示).5. 已知抛物线 与 轴交于点 和点 两点,与 轴交于点 . (1)、求抛物线的解析式;(2)、点 是抛物线上一动点(不与点 , , 重合),作 轴,垂足为 ,连接 .
(1)、求抛物线的解析式;(2)、点 是抛物线上一动点(不与点 , , 重合),作 轴,垂足为 ,连接 .①如图1,若点 在第三象限,且 ,求点 的坐标;
②直线 交直线 于点 ,当点 关于直线 的对称点 落在 轴上时,求四边形 的周长.
6. 在平面直角坐标系中,O为坐标原点,抛物线与y轴交于点. (1)、直接写出抛物线的解析式.(2)、如图,将抛物线向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由.(3)、直线BC与抛物线交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与相似,若存在,请求出点T的坐标;若不存在,请说明理由.(4)、若将抛物线进行适当的平移,当平移后的抛物线与直线BC最多只有一个公共点时,请直接写出拋物线平移的最短距离并求出此时抛物线的顶点坐标.7. 如图,在平面直角坐标系中,已知抛物线的顶点为A,与y轴交于点C,线段轴,交该抛物线于另一点B.
(1)、直接写出抛物线的解析式.(2)、如图,将抛物线向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由.(3)、直线BC与抛物线交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与相似,若存在,请求出点T的坐标;若不存在,请说明理由.(4)、若将抛物线进行适当的平移,当平移后的抛物线与直线BC最多只有一个公共点时,请直接写出拋物线平移的最短距离并求出此时抛物线的顶点坐标.7. 如图,在平面直角坐标系中,已知抛物线的顶点为A,与y轴交于点C,线段轴,交该抛物线于另一点B. (1)、求点B的坐标及直线的解析式:(2)、当二次函数的自变量x满足时,此函数的最大值为p,最小值为q,且.求m的值:(3)、平移抛物线 , 使其顶点始终在直线上移动,当平移后的抛物线与射线BA只有一个公共点时,设此时抛物线的顶点的横坐标为n,请直接写出n的取值范围.8. 如图1,平面直角坐标系xOy中,抛物线与x轴分则点A和点 , 与y轴交于点C,对称轴为直线 , 且 , P为抛物线上一动点.
(1)、求点B的坐标及直线的解析式:(2)、当二次函数的自变量x满足时,此函数的最大值为p,最小值为q,且.求m的值:(3)、平移抛物线 , 使其顶点始终在直线上移动,当平移后的抛物线与射线BA只有一个公共点时,设此时抛物线的顶点的横坐标为n,请直接写出n的取值范围.8. 如图1,平面直角坐标系xOy中,抛物线与x轴分则点A和点 , 与y轴交于点C,对称轴为直线 , 且 , P为抛物线上一动点.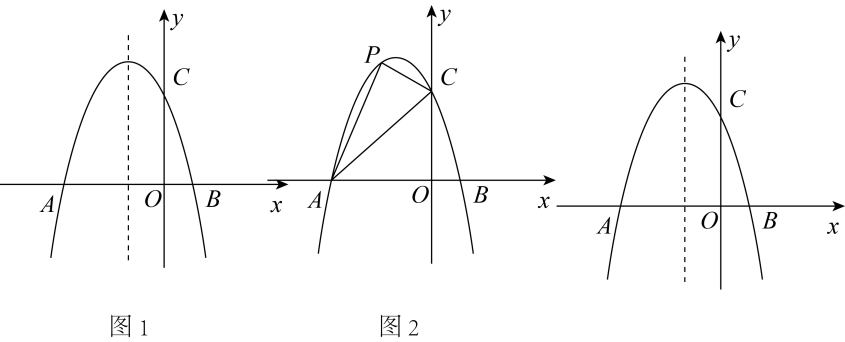 (1)、直接写出抛物线的解析式;(2)、如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;(3)、设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.9. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)、直接写出抛物线的解析式;(2)、如图2,连接AC,当点P在直线AC上方时,求四边形PABC面积的最大值,并求出此时P点的坐标;(3)、设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.9. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.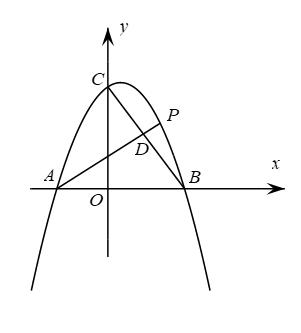 (1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,
(1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,①当与x轴平行时,求的值;
②当与x轴不平行时,求的最大值;
(3)、连接 , 是否存在点P,使得 , 若存在,求m的值,若不存在,请说明理由.10. 在平面直角坐标系中,直线y=mx-2m与x轴,y轴分别交于A,B两点,顶点为D的抛物线y=-x2+2mx-m2+2与y轴交于点C.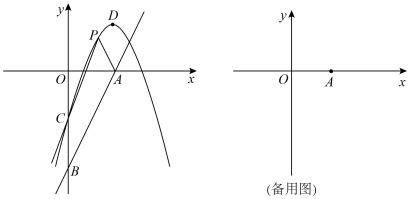 (1)、如图,当m=2时,点P是抛物线CD段上的一个动点.
(1)、如图,当m=2时,点P是抛物线CD段上的一个动点.①求A,B,C,D四点的坐标;
②当△PAB面积最大时,求点P的坐标;
(2)、在y轴上有一点M(0,m),当点C在线段MB上时,①求m的取值范围;
②求线段BC长度的最大值.
二、综合题
-
11. 综合与探究:如图,在平面直角坐标系中,抛物线的顶点为点D,与x轴交于点A和点B,其中B的坐标为.直线l与抛物线交于B,C两点,其中点C的坐标为.
 (1)、求抛物线和直线l的解析式;(2)、直线l与抛物线的对称轴交于点E,P为线段上一动点(点P不与点B,C重合),过点P作交抛物线于点F,设点P的横坐标为t.当t为何值时,四边形是平行四边形?(3)、在(2)的条件下,设的面积为S,当t为何值时,S最大?最大值是多少?12. 如图,在平面直角坐标系中,抛物线经过点 , 点M为抛物线的顶点,点B在y轴上,直线与抛物线在第一象限交于点.
(1)、求抛物线和直线l的解析式;(2)、直线l与抛物线的对称轴交于点E,P为线段上一动点(点P不与点B,C重合),过点P作交抛物线于点F,设点P的横坐标为t.当t为何值时,四边形是平行四边形?(3)、在(2)的条件下,设的面积为S,当t为何值时,S最大?最大值是多少?12. 如图,在平面直角坐标系中,抛物线经过点 , 点M为抛物线的顶点,点B在y轴上,直线与抛物线在第一象限交于点. (1)、求抛物线的解析式;(2)、连接 , 点Q是直线上不与A、B重合的点,若 , 请求出点Q的坐标;(3)、在x轴上有一动点H,平面内是否存在一点N,使以点A、H、C、N为顶点的四边形是菱形?若存在,直接写出点N的坐标,若不存在,请说明理由.13. 如图,已知抛物线:交x轴于点 , 交y轴于点C.
(1)、求抛物线的解析式;(2)、连接 , 点Q是直线上不与A、B重合的点,若 , 请求出点Q的坐标;(3)、在x轴上有一动点H,平面内是否存在一点N,使以点A、H、C、N为顶点的四边形是菱形?若存在,直接写出点N的坐标,若不存在,请说明理由.13. 如图,已知抛物线:交x轴于点 , 交y轴于点C.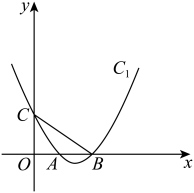 (1)、直接写出点的坐标;(2)、将直线向下平移m个单位,使直线与抛物线恰好只有一个公共点,求m的值;(3)、在抛物线上存在点D,使 , 求点D的坐标.14. 如图,在平面直角坐标系中,已知直线与x轴交于点A,与y轴交于点B,过A、B两点的抛物线与x轴交于另一点.
(1)、直接写出点的坐标;(2)、将直线向下平移m个单位,使直线与抛物线恰好只有一个公共点,求m的值;(3)、在抛物线上存在点D,使 , 求点D的坐标.14. 如图,在平面直角坐标系中,已知直线与x轴交于点A,与y轴交于点B,过A、B两点的抛物线与x轴交于另一点. (1)、求抛物线的解析式;(2)、在抛物线上是否存在一点P,使?若存在,请求出点P的坐标,若不存在,请说明理由;(3)、点M为直线下方抛物线上一点,点N为y轴上一点,当的面积最大时,求的最小值.15. 如图,抛物线y=-x2+bx+c与x轴相交于A、B(3,0)两点,与y轴交于点C(0,3),顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F.
(1)、求抛物线的解析式;(2)、在抛物线上是否存在一点P,使?若存在,请求出点P的坐标,若不存在,请说明理由;(3)、点M为直线下方抛物线上一点,点N为y轴上一点,当的面积最大时,求的最小值.15. 如图,抛物线y=-x2+bx+c与x轴相交于A、B(3,0)两点,与y轴交于点C(0,3),顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F. (1)、求抛物线和直线AC的解析式;(2)、在抛物线上是否存在点P,使以点A、C、P为顶点的三角形是直角三角形,且AP为斜边?若存在,求出点P的坐标;若不存在,说明理由.(3)、设过E的直线与抛物线相交于点M(x1 , y1),N(x2 , y2),求|x1-x2|的最小值.16. 抛物线与轴交于点 , (在左边),与轴交于点.(1)、直接写出 , , 点的坐标;(2)、如图,在第三象限的抛物线上求点 , 使;
(1)、求抛物线和直线AC的解析式;(2)、在抛物线上是否存在点P,使以点A、C、P为顶点的三角形是直角三角形,且AP为斜边?若存在,求出点P的坐标;若不存在,说明理由.(3)、设过E的直线与抛物线相交于点M(x1 , y1),N(x2 , y2),求|x1-x2|的最小值.16. 抛物线与轴交于点 , (在左边),与轴交于点.(1)、直接写出 , , 点的坐标;(2)、如图,在第三象限的抛物线上求点 , 使;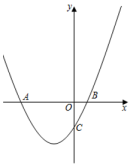 (3)、如图,点为第一象限的抛物线上的一点,过点作交抛物线于另一点 , 交轴于点 , 且满足 , 求的解析式.
(3)、如图,点为第一象限的抛物线上的一点,过点作交抛物线于另一点 , 交轴于点 , 且满足 , 求的解析式. 17. 如图1,二次函数的图像与x轴交于点 , , 与y轴交于点C.
17. 如图1,二次函数的图像与x轴交于点 , , 与y轴交于点C. (1)、求二次函数的解析式;(2)、点P为抛物线上一动点.
(1)、求二次函数的解析式;(2)、点P为抛物线上一动点.①如图2,过点C作x轴的平行线与抛物线交于另一点D,连接 , .当时,求点P的坐标;
②如图3,若点P在直线上方的抛物线上,连接与交于点E,求的最大值.
18. 如图,已知抛物线与x轴交于A、两点,与y轴交于.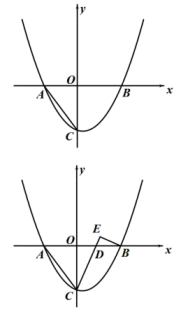 (1)、求点A的坐标;(2)、点P在抛物线上,若 , 求出点P的坐标;(3)、如图2,点D在线段上,直线于点E,当时,直接写出点D的坐标.19. 如图1,抛物线交x轴于A、B两点(A在B左侧),交y轴于点C,.
(1)、求点A的坐标;(2)、点P在抛物线上,若 , 求出点P的坐标;(3)、如图2,点D在线段上,直线于点E,当时,直接写出点D的坐标.19. 如图1,抛物线交x轴于A、B两点(A在B左侧),交y轴于点C,. (1)、求抛物线的解析式;(2)、如图2,点T在抛物线上,且 , 求点T的坐标;(3)、如图3,将线段绕点C逆时针旋转至(),轴于H,点P为的内心,直接写出的最小值 .20. 如图,已知抛物线y=x2+bx+c与x轴交于点A(2,0),B(-4,0),与y轴交于C(0,-3),连接BC.
(1)、求抛物线的解析式;(2)、如图2,点T在抛物线上,且 , 求点T的坐标;(3)、如图3,将线段绕点C逆时针旋转至(),轴于H,点P为的内心,直接写出的最小值 .20. 如图,已知抛物线y=x2+bx+c与x轴交于点A(2,0),B(-4,0),与y轴交于C(0,-3),连接BC.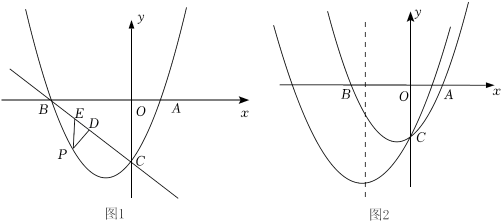 (1)、求抛物线的解析式;(2)、如图1,点P是直线BC下方抛物线上一点,过点P作PD⊥BC于点D,过点P作PE∥y轴交BC于点E,求△PDE周长的最大值及此时点P的坐标;(3)、如图2,将抛物线沿射线AC方向平移,平移后的抛物线与原抛物线相交于点C,在平移后的抛物线的对称轴上是否存在一点F,使得以点B、C、F为顶点的三角形为等腰三角形,若存在,请直接写出点F的坐标;若不存在,请说明理由.21. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,抛物线的对称轴是直线 , 且经过A、C两点与x轴的另一交点为B.
(1)、求抛物线的解析式;(2)、如图1,点P是直线BC下方抛物线上一点,过点P作PD⊥BC于点D,过点P作PE∥y轴交BC于点E,求△PDE周长的最大值及此时点P的坐标;(3)、如图2,将抛物线沿射线AC方向平移,平移后的抛物线与原抛物线相交于点C,在平移后的抛物线的对称轴上是否存在一点F,使得以点B、C、F为顶点的三角形为等腰三角形,若存在,请直接写出点F的坐标;若不存在,请说明理由.21. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,抛物线的对称轴是直线 , 且经过A、C两点与x轴的另一交点为B. (1)、①直接写出点B的坐标;②求抛物线的解析式;(2)、点E为直线上方抛物线上的一动点,过点E作x轴于点G,交于点D,连接 , 当四边形面积最大时,求出E点的坐标.(3)、抛物线上是否存在点M,过点M作轴于点N,使得以点A、M、N为顶点的与相似?若存在,直接写出点M的坐标,若不存在,请说明理由.
(1)、①直接写出点B的坐标;②求抛物线的解析式;(2)、点E为直线上方抛物线上的一动点,过点E作x轴于点G,交于点D,连接 , 当四边形面积最大时,求出E点的坐标.(3)、抛物线上是否存在点M,过点M作轴于点N,使得以点A、M、N为顶点的与相似?若存在,直接写出点M的坐标,若不存在,请说明理由.