备考2023年中考数学压轴题训练 ——二次函数（3）

试卷更新日期：2023-05-14 类型：三轮冲刺

进入出卷网下载

一、真题

1. 如图，在平面直角坐标系中，抛物线 $y = x^{2} + b x + c$ （ $b$ ， $c$ 是常数）经过点 $A (1 ， 0)$ ，点 $B (0 ， 3)$ ．点 $P$ 在此抛物线上，其横坐标为 $m$ ．

(1)、求此抛物线的解析式；

(2)、当点 $P$ 在 $x$ 轴上方时，结合图象，直接写出 $m$ 的取值范围；

(3)、若此抛物线在点 $P$ 左侧部分（包括点 $P$ ）的最低点的纵坐标为 $2 - m$ ．
①求 $m$ 的值；
②以 $P A$ 为边作等腰直角三角形 $P A Q$ ，当点 $Q$ 在此抛物线的对称轴上时，直接写出点 $Q$ 的坐标．

查看试题解析
2. 在平面直角坐标系中，抛物线 $y = x^{2} - b x$ （b是常数）经过点 $(2 ， 0)$ ．点A在抛物线上，且点A的横坐标为m（ $m \neq 0$ ）．以点A为中心，构造正方形 $P Q M N$ ， $P Q = 2 | m |$ ，且 $P Q ⊥ x$ 轴．

(1)、求该抛物线对应的函数表达式：

(2)、若点B是抛物线上一点，且在抛物线对称轴左侧．过点B作x轴的平行线交抛物线于另一点C，连接 $B C$ ．当 $B C = 4$ 时，求点B的坐标；

(3)、若 $m > 0$ ，当抛物线在正方形内部的点的纵坐标y随x的增大而增大时，或者y随x的增大而减小时，求m的取值范围；

(4)、当抛物线与正方形 $P Q M N$ 的边只有2个交点，且交点的纵坐标之差为 $\frac{3}{4}$ 时，直接写出m的值．

查看试题解析
3. 为落实“双减”，老师布置了一项这样的课后作业：

二次函数的图象经过点 $(- 1 ， - 1)$ ，且不经过第一象限，写出满足这些条件的一个函数表达式．

(1)、 [观察发现]
请完成作业，并在直角坐标系中画出大致图象．

(2)、[思考交流]
小亮说：“满足条件的函数图象的对称轴一定在y轴的左侧．”
小莹说：“满足条件的函数图象一定在x轴的下方．”
你认同他们的说法吗？若不认同，请举例说明．

(3)、[概括表达]
小博士认为这个作业的答案太多，老师不方便批阅，于是探究了二次函数 $y = a x^{2} + b x + c$ 的图象与系数a，b，c的关系，得出了提高老师作业批阅效率的方法．

请你探究这个方法，写出探究过程．

查看试题解析
4. 如图1，抛物线 $y = x^{2} + b x + c$ 与x轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与y轴交于点C.
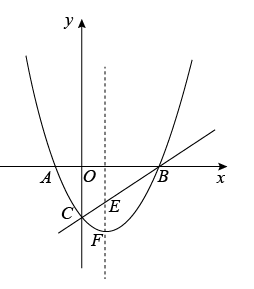
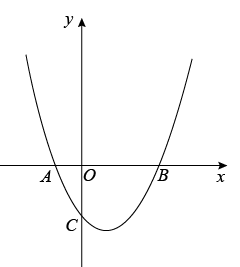
图1 图2

(1)、求该抛物线的解析式；

(2)、若点E是抛物线的对称轴与直线BC的交点，点F是抛物线的顶点，求EF的长；

(3)、设点P是（1）中抛物线上的一个动点，是否存在满足 $S_{△ P A B} = 6$ 的点P？如果存在，请求出点P的坐标；若不存在，请说明理由.（请在图2中探讨）

查看试题解析
5. 如图，在平面直角坐标系中，抛物线 $y = x^{2} - 2 x - 3$ 与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，连接 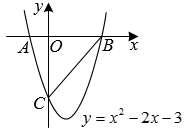$A C ， B C$ ．

(1)、求线段AC的长；

(2)、若点Р为该抛物线对称轴上的一个动点，当 $P A = P C$ 时，求点P的坐标；

(3)、若点M为该抛物线上的一个动点，当 $△ B C M$ 为直角三角形时，求点M的坐标．

查看试题解析
6. 如图，在直角坐标系中，二次函数 $y = - x^{2} + b x + c$ 的图象与x轴交于A，B两点，与y轴交于点 $C (0 ， 3)$ ，对称轴为直线 $x = - 1$ ，顶点为点D．

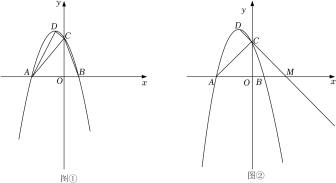(1)、求二次函数的表达式；

(2)、连接DA，DC，CB，CA，如图①所示，求证： $∠ D A C = ∠ B C O$ ；

(3)、如图②，延长DC交x轴于点M，平移二次函数 $y = - x^{2} + b x + c$ 的图象，使顶点D沿着射线DM方向平移到点 $D_{1}$ 且 $C D_{1} = 2 C D$ ，得到新抛物线 $y_{1}$ ， $y_{1}$ 交y轴于点N．如果在 $y_{1}$ 的对称轴和 $y_{1}$ 上分别取点P，Q，使以MN为一边，点M，N，P，Q为顶点的四边形是平行四边形，求此时点Q的坐标．

查看试题解析
7. 如图，已知直线y＝ $\frac{4}{3}$ x+4与x轴交于点A，与y轴交于点C，抛物线y＝ax²+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝﹣1．

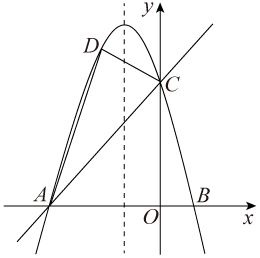(1)、求抛物线的表达式；

(2)、D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；

(3)、若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．

查看试题解析
8. 在平面直角坐标系xOy中，已知抛物线y=-x²+2mx+3m，点A（3，0）．

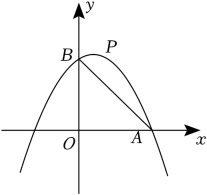(1)、当抛物线过点A时，求抛物线的解析式；

(2)、证明：无论m为何值，抛物线必过定点D，并求出点D的坐标；

(3)、在（1）的条件下，抛物线与y轴交于点B，点P是抛物线上位于第一象限的点，连接AB，PD交于点M，PD与y轴交于点N．设S=S△PAM－S△BMN，问是否存在这样的点P，使得S有最大值？若存在，请求出点P的坐标，并求出S的最大值；若不存在，请说明理由．

查看试题解析
9. 如图，抛物线y＝-x²+bx+c与x轴相交于A，B两点（点A在点B的左侧），顶点D（1，4）在直线l：y＝ $\frac{4}{3}$ x+t上，动点P（m，n）在x轴上方的抛物线上．

(1)、求这条抛物线对应的函数表达式；

(2)、过点P作PM⊥x轴于点M，PN⊥l于点N，当1＜m＜3时，求PM+PN的最大值；

(3)、设直线AP，BP与抛物线的对称轴分别相交于点E，F，请探索以A，F，B，G（G是点E关于x轴的对称点）为顶点的四边形面积是否随着P点的运动而发生变化，若不变，求出这个四边形的面积；若变化，说明理由．

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + 3$ 与x轴交于点 $A (3 ， 0)$ ，与y轴交于点B，点C在直线AB上，过点C作 $C D ⊥ x$ 轴于点 $D (1 ， 0)$ ，将 $△ A C D$ 沿CD所在直线翻折，使点A恰好落在抛物线上的点E处．

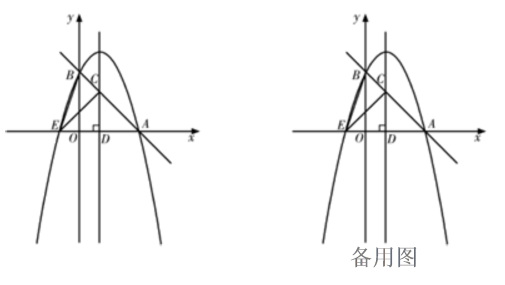(1)、求抛物线解析式；

(2)、连接BE，求 $△ B C E$ 的面积；

(3)、拋物线上是否存在一点P，使 $∠ P E A = ∠ B A E$ ？若存在，求出P点坐标；若不存在，请说明理由．

查看试题解析

二、综合题

11. 在平面直角坐标系中，过点 $(0 ， 5)$ 且平行于x轴的直线与直线 $y = x$ 交于点P，点P关于直线 $x = 2$ 的对称点为点Q，抛物线 $y = a x^{2} + b x$ 经过点P、Q．

(1)、点P的坐标为；点Q的坐标为．

(2)、求抛物线 $y = a x^{2} + b x$ 的表达式．

(3)、若点A在抛物线 $y = a x^{2} + b x$ 上，且点A横坐标为2m．过点A向直线 $x = 2$ 作垂线，设垂足为B，当点A与点B不重合时，以 $A B$ 为边向下作矩形 $A B C D$ ，使 $B C = 4 A B$ ．
①当矩形 $A B C D$ 的中心恰好落在抛物线 $y = a x^{2} + b x$ 上时，求m的值．
②当抛物线 $y = a x^{2} + b x$ 恰与 $B C$ 有交点时，设该交点为E，若 $c o s ∠ B A E = \frac{\sqrt{5}}{5}$ ，直接写出m的值．

查看试题解析
12. 如图，抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于 $A (- 1 ， 0)$ ， $B (5 ， 0)$ 两点．直线 $l$ 过点 $A$ 且在第一象限与抛物线相交于点 $C$ ．

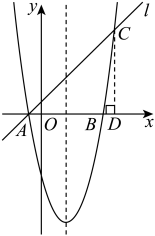(1)、①求此抛物线的函数解析式；②当 $y < 0$ 时，自变量 $x$ 的取值范围 ▲ ；

(2)、设点 $C$ 的横坐标为 $m$ ，作 $C D ⊥ x$ 轴于 $D$ ．
①当 $△ A C D$ 为等腰直角三角形时，点 $C$ 的纵坐标为 ▲ （用含 $m$ 的式子表示）；
②在①题的条件下，求出点 $C$ 的坐标．

查看试题解析
13. 如图，抛物线 $y = a x^{2} - 3 x + c$ 与x轴交于 $A (- 4 ， 0)$ ， B两点，与y轴交于点 $C (0 ， 4)$ ，点D为x轴上方抛物线上的动点，射线 $O D$ 交直线 $A C$ 于点E，将射线 $O D$ 绕点O逆时针旋转 $45 °$ 得到射线 $O P$ ， $O P$ 交直线 $A C$ 于点F，连接 $D F$ ．

(1)、求抛物线的解析式；

(2)、当点D在第二象限且 $\frac{D E}{E O} = \frac{3}{4}$ 时，求点D的坐标；

(3)、当 $△ O D F$ 为直角三角形时，请直接写出点D的坐标．

查看试题解析
14. 在平面直角坐标系中，抛物线 $y = x^{2} + b x - 1$ （b是常数）的对称轴为直线 $x = - 1$ ，点A在这个抛物线上，且点A的横坐标为m．

(1)、求该抛物线对应的函数表达式，并写出顶点C的坐标．

(2)、点B在这个抛物线上（点B在点A的左侧），点B的横坐标为 $- 1 - 2 m$ ．
①当 $△ A B C$ 是以 $A B$ 为底的等腰三角形时，求 $△ A B C$ 的面积．
②将此抛物线A、B两点之间的部分（包括A、B两点）记为图象G，当顶点C在图象G上，记图象G最高点的纵坐标与最低点的纵坐标的差为h，求h与m之间的函数关系式．

(3)、设点D的坐标为 $(m ， 2 - m)$ ，点E的坐标为 $(1 - m ， 2 - m)$ ，点F在坐标平面内，以A、D、E、F为顶点构造矩形，当此抛物线与矩形有3个交点时，直接写出m的取值范围．

查看试题解析
15. 在平面直角坐标系中，抛物线 $y = x^{2} + b x + c$ （ $a \neq 0$ ， $a$ 、 $b$ 、 $c$ 为常数）与 $x$ 轴交点坐标为 $(1 ， 0)$ ，与 $y$ 轴交点的坐标为 $(0 ， 3)$ ，点 $A$ 、点 $B$ 均在这个抛物线上，点 $A$ 的横坐标为 $m$ ，点 $B$ 的横坐标为 $1 - m$ ．当 $B$ 在 $A$ 的左侧时，抛物线上 $A$ 、 $B$ 两点之间的部分（包括 $A$ 、 $B$ 两点）记为图象 $G$ ．

(1)、求此抛物线对应的函数表达式．

(2)、当图象 $G$ 对应的函数值 $y$ 随 $x$ 的增大而减小时，求 $m$ 的取值范围．

(3)、图象 $G$ 最大值与最小值差为 $h$ ，求 $h$ 与 $m$ 之间的函数关系式．

(4)、设点 $E$ 的坐标为 $(m - 3 ， 2)$ ，点 $F$ 的坐标 $(m - 3 ， m - 3)$ ，连结 $E F$ ，以 $E F$ 为边长向右作正方形 $E F P Q$ ，当抛物线与正方形 $E F P Q$ 的边只有两个交点，且交点的纵坐标之差为1时，直接写出 $m$ 的值．

查看试题解析
16. 如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法： $S_{△ A B C} = \frac{1}{2} a h$ ，即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题：

如图2，抛物线顶点坐标为点C(1，4)，交x轴于点A(3，0)，交y轴于点B.

(1)、求抛物线和直线AB的解析式；

(2)、点P是抛物线(在第一象限内)上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及 $S_{Δ C A B}$ ；

(3)、是否存在一点P，使S_△PAB= $\frac{9}{8}$ S_△CAB，若存在，求出P点的坐标；若不存在，请说明理由.

查看试题解析
17. 图1，在平面直角坐标系 $x O y$ 中，已知抛物线 $y = - x^{2} + b x + c$ 经过 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点．P是抛物线上一点，且在直线 $B C$ 的上方．

(1)、求抛物线的解析式；

(2)、如图2，点E为 $O C$ 中点，作 $P Q ∥ y$ 轴交 $B C$ 于点Q，若四边形 $C P Q E$ 为平行四边形，求点P的横坐标；

(3)、如图3，连结 $A C 、 A P$ ， $A P$ 交 $B C$ 于点M，作 $P H ∥ A C$ 交 $B C$ 于点H．记 $△ P H M$ ， $△ P M C$ ， $△ C A M$ 的面积分别为 $S_{1} ， S_{2} ， S_{3}$ ．判断 $\frac{S_{1}}{S_{2}} + \frac{S_{2}}{S_{3}}$ 是否存在最大值，若存在，求出最大值；若不存在，请说明理由．

查看试题解析
18. 如图1，在平面直角坐标系中，抛物线 $y = a {(x - 3)}^{2} + 4$ 过原点，与x轴的正半轴交于点A，已知B点为抛物线的顶点，抛物线的对称轴与x轴交于点D．

(1)、求a的值，并直接写出A、B两点的坐标；

(2)、若P点是该抛物线对称轴上一点，且 $∠ B O P = 45 °$ ，求点P的坐标；

(3)、如图2，若C点为线段 $B D$ 上一点，求 $3 B C + 5 A C$ 的最小值．

查看试题解析
19. 如图，已知抛物线 $y = a x^{2} + 2 x + c$ 交x轴于点 $A (- 1 ， 0)$ 和点 $B (3 ， 0)$ ，交y轴于点C，点D与点C关于抛物线的对称轴对称．

(1)、求该抛物线的表达式，并求出点D的坐标；

(2)、若点E为该抛物线上的点，点F为直线 $A D$ 上的点，若 $E F ∥ x$ 轴，且 $E F = 1$ （点E在点F左侧），求点E的坐标；

(3)、若点P是该抛物线对称轴上的一个动点，是否存在点P，使得 $△ A P D$ 为直角三角形？若不存在，请说明理由；若存在，直接写出点P坐标．

查看试题解析
20. 抛物线L： $y = - x^{2} + b x + c$ 经过点 $A (0 ， 3)$ ，与它的对称轴直线 $x = 1$ 交于点B．

(1)、求抛物线L的解析式；

(2)、抛物线L与x正半轴交于点N，E在直线 $A N$ 上方的抛物线上，过点E作 $E H ⊥ A N$ ，垂足为H，求 $E H$ 的最大值；

(3)、如图2，将抛物线L向上平移 $m$ （ $m > - 3$ ，当 $m < 0$ 时，表示向下平移 $| m |$ ）个单位长度得到抛物线 $L_{1}$ ，抛物线 $L_{1}$ 与y轴交于点C，过点C作y轴的垂线交抛物线 $L_{1}$ 于另一点D，F为抛物线 $L_{1}$ 的对称轴与x轴的交点，P为线段 $O C$ 上一点．若 $△ P C D$ 与 $△ P O F$ 相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标．

查看试题解析
21. 如图①，抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴交于两点 $A$ ， $B (4 ， 0)$ （点 $A$ 位于点 $B$ 的左侧），与 $y$ 轴交于点 $C (0 ， 4)$ ，拋物线的对称轴 $l$ 与 $x$ 轴交于点 $N$ ，长为2的线段 $P Q$ （点 $P$ 位于点 $Q$ 的上方）在 $x$ 轴上方的抛物线对称轴上运动．

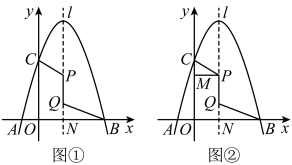(1)、求抛物线的关系式；

(2)、在线段 $P Q$ 运动过程中，当 $P C + P A$ 的值最小时，求此时点 $P$ 的坐标；

(3)、如图②过点 $P$ 作 $P M ⊥ y$ 轴于点 $M$ ，当 $△ C P M$ 和 $△ Q B N$ 相似时，求点 $Q$ 的坐标．

查看试题解析
22. 抛物线 $y = a x^{2} + b x + 4 (a \neq 0)$ 与x轴交于A，B两点，与y轴交于点C，点B的坐标为 $(4 ， 0)$ ，抛物线的对称轴为 $x = 1$ ，直线AD交抛物线于点 $D (2 ， m)$ ．

(1)、求抛物线和直线 $A D$ 的解析式；

(2)、如图1，点Q是线段 $A B$ 上一动点，过点Q作 $Q E ∥ A D$ ，交 $B D$ 于点E，连接 $D Q$ ，若点Q的坐标为 $(m ， 0)$ ，求 $△ Q E D$ 的面积S与m的函数表达式，并写出S是否存在最大值？若存在，求出S的最大值，并直接写出此时点E的坐标；

(3)、如图2，直线 $A D$ 交y轴于点F，点M为抛物线对称轴上的动点，点N在x轴上，当四边形 $C M N F$ 周长取最小值时，求出满足条件的点M和点N的坐标．

查看试题解析
23. 抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 与 $x$ 轴交于点 $A (- 2 ， 0)$ 和 $B (4 ， 0)$ ，与 $y$ 轴交于点 $C$ ，连接 $B C$ ．点 $P$ 是线段 $B C$ 下方抛物线上的一个动点（不与点 $B$ ， $C$ 重合），过点 $P$ 作 $y$ 轴的平行线交 $B C$ 于 $M$ ，交 $x$ 轴于 $N$ ，设点 $P$ 的横坐标为 $t$ ．

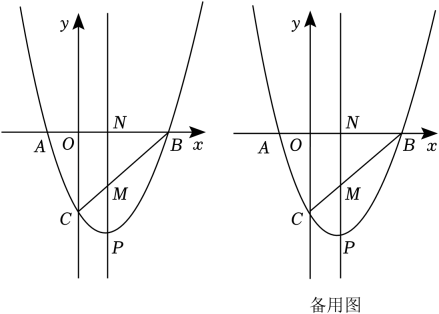(1)、求该抛物线的解析式；

(2)、用关于 $t$ 的代数式表示线段 $P M$ ，求 $P M$ 的最大值及此时点 $M$ 的坐标；

(3)、过点 $C$ 作 $C H ⊥ P N$ 于点 $H$ ， $S_{△ B M N} = 9 S_{△ C H M}$ ，
①求点 $P$ 的坐标；
②连接 $C P$ ，在 $y$ 轴上是否存在点 $Q$ ，使得 $△ C P Q$ 为直角三角形，若存在，求出点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 经过 $A (- 2 ， 0)$ ，与y轴交于点 $B (0 ， 4)$ ，直线 $x = 3$ 与x轴交于点C．

(1)、求该抛物线的解析式；

(2)、正比例函数 $y = k x$ 的图象分别与线段 $A B$ ，直线 $x = 3$ 交于点D，E，当 $△ B D O$ 与 $△ O C E$ 相似时，求线段 $O D$ 的长度；

(3)、如图2，P是抛物线上位于第一象限的一个动点，在线段 $O C$ 和直线 $x = 3$ 上是否分别存在点F，G，使B，F，G，P为顶点的四边形是以 $B F$ 为一边的矩形，若存在，求出点F的坐标，若不存在，说明理由．

查看试题解析
25. 已知抛物线 $y = - x^{2} + b x + c$ 经过 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ，

(1)、求抛物线的解析式和顶点坐标；

(2)、当 $0 \leq x \leq 3$ 时，直接写出 $y_{最小值} =$ ， $y_{最大值} =$ ；

(3)、点P是抛物线上第一象限内的一点，若 $S_{△ A C P} = 3$ ，求点P的坐标．

查看试题解析
26. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 4 (a \neq 0)$ 与x轴交于点 $A (- 1 ， 0) ， B (4 ， 0) ，$ 与y轴交于点C．

(1)、求该抛物线的解析式：

(2)、直线l为该抛物线的对称轴，点D与点C关于直线l对称，点F为直线 $A D$ 下方抛物线上一动点，连接 $F A ， F D$ ，求 $△ F A D$ 面积的最大值：

(3)、在（2）的条件下，将抛物线 $y = a x^{2} + b x - 4 (a \neq 0)$ 沿射线 $A D$ 平移4 $\sqrt{2}$ 个单位，得到新的抛物线 $y_{1}$ ，点E为点F的对应点，点P为 $y_{1}$ 的对称轴上任意一点，在 $y_{1}$ 上确定一点Q，使得以点D，E，P，Q为顶点的四边形是平行四边形，请直接写出所有符合条件的点Q的坐标．

查看试题解析
27. 如图1，直线 $y = - x + 5$ 与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线与x轴的另一交点坐标为 $A （ - 1 ， 0 ）$ .

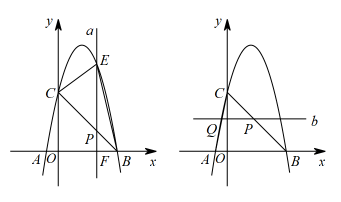(1)、求B、C两点的坐标及该抛物线所对应的函数关系式；

(2)、P在线段 $B C$ 上的一个动点（与B、C不重合），过点P作直线 $a ∥ y$ 轴，交抛物线于点E，交x轴于点F，设点P的横坐标为m.
①若点P的横坐标为m，请用m表示线段 $P E$ 的长度并写出m的取值范围；
②有人认为：当直线a与抛物线的对称轴重合时，线段 $P E$ 的值最大，你同意他的观点吗？请说明理由；
③过点P作直线 $b ∥ x$ 轴（图2），交 $A C$ 于点Q，那么在x轴上是否存在点R，使得 $△ P Q R$ 与 $△ B O C$ 相似？若存在，请求出点R的坐标；若不存在，请说明理由.

查看试题解析
28. 如图1所示，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c$ 经过 $A (- 3 ， 0)$ 、 $B (1 ， 0)$ 、 $C (0 ， 3)$ 三点．

(1)、求抛物线的函数解析式

(2)、如图2，点D为抛物线的顶点，连接AD，点P是线段AD上一个动点（不与A、D重合），过点P作y轴的垂线，垂足点为E，连接AE．如果P点的坐标为 $(x ， y)$ ， $△ P A E$ 的面积为S，求S与x之间的函数关系式（不用写出自变量x的取值范围）；

(3)、在（2）的条件下，当S取到最大值时，过点P作x轴的垂线，垂足为F，连接EF，把 $△ P E F$ 沿直线EF折叠，点P的对应点为点 $P^{'}$ ，求出 $P^{'}$ 的坐标．

查看试题解析
29. 如图1，抛物线 $y = a x^{2} + \frac{3}{2} x + c$ 与x轴交于点A、 $B (4 ， 0)$ （A点在B点左侧），与y轴交于点 $C (0 ， 6)$ ，点P是抛物线上一个动点，连接 $P B ， P C ， B C$

(1)、求抛物线的函数表达式；

(2)、如图2所示，当点P在直线 $B C$ 上方运动时，连接 $A C$ ，求四边形 $A B P C$ 面积的最大值，并写出此时P点坐标．

(3)、若点M是x轴上的一个动点，点N是抛物线上一动点，P的横坐标为 $3$ ．试判断是否存在这样的点M，使得以点 $B ， M ， N ， P$ 为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由．

查看试题解析