备考2023年中考数学压轴题训练 ——解直角三角形

试卷更新日期：2023-05-14 类型：三轮冲刺

进入出卷网下载

一、真题

1. 如图

【问题情境】

在一次数学兴趣小组活动中，小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中 $∠ A C B = ∠ D E B = 90 °$ ， $∠ B = 30 °$ ， $B E = A C = 3$ .

【问题探究】

小昕同学将三角板 $D E B$ 绕点 $B$ 按顺时针方向旋转.

(1)、如图2，当点 $E$ 落在边 $A B$ 上时，延长 $D E$ 交 $B C$ 于点 $F$ ，求 $B F$ 的长.

(2)、若点 $C$ 、 $E$ 、 $D$ 在同一条直线上，求点 $D$ 到直线 $B C$ 的距离.

(3)、连接 $D C$ ，取 $D C$ 的中点 $G$ ，三角板 $D E B$ 由初始位置（图1），旋转到点 $C$ 、 $B$ 、 $D$ 首次在同一条直线上（如图3），求点 $G$ 所经过的路径长.

(4)、如图4， $G$ 为 $D C$ 的中点，则在旋转过程中，点 $G$ 到直线 $A B$ 的距离的最大值是.

查看试题解析
2. 如图，在锐角△ABC中，∠A=60°，点D，E分别是边AB，AC上一动点，连接BE交直线CD于点F．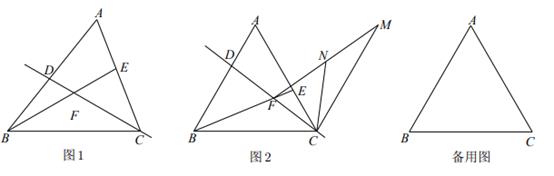

(1)、如图1，若AB>AC，且BD=CE，∠BCD=∠CBE，求∠CFE的度数；

(2)、如图2，若AB=AC，且BD=AE，在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM，连接MF，点N是MF的中点，连接CN．在点D，E运动过程中，猜想线段BF，CF，CN之间存在的数量关系，并证明你的猜想；

(3)、若AB=AC，且BD=AE，将△ABC沿直线AB翻折至△ABC所在平面内得到△ABP，点H是AP的中点，点K是线段PF上一点，将△PHK沿直线HK翻折至△PHK所在平面内得到△QHK，连接PQ．在点D，E运动过程中，当线段PF取得最小值，且QK⊥PF时，请直接写出 $\frac{P Q}{B C}$ 的值．

查看试题解析
3. 如图，直线 $y = \frac{3}{4} x + 6$ 分别与x轴、y轴交于点A、B，点C为线段 $A B$ 上一动点（不与A、B重合），以C为顶点作 $∠ O C D = ∠ O A B$ ，射线 $C D$ 交线段 $O B$ 于点D，将射线 $O C$ 绕点O顺时针旋转 $90 °$ 交射线 $C D$ 于点E，连接 $B E$ .

(1)、证明： $\frac{C D}{D B} = \frac{O D}{D E}$ ；（用图1）

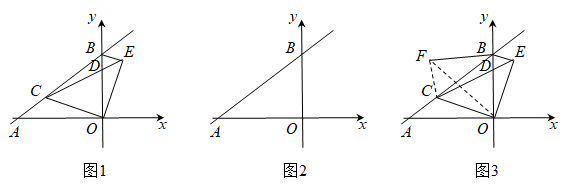(2)、当 $△ B D E$ 为直角三角形时，求 $D E$ 的长度；（用图2）

(3)、点A关于射线 $O C$ 的对称点为F，求 $B F$ 的最小值.（用图3）

查看试题解析
4. 在数学兴趣小组活动中，同学们对菱形的折叠问题进行了探究.如图（1），在菱形 $A B C D$ 中， $∠ B$ 为锐角， $E$ 为 $B C$ 中点，连接 $D E$ ，将菱形 $A B C D$ 沿 $D E$ 折叠，得到四边形 $A^{'} B^{'} E D$ ，点 $A$ 的对应点为点 $A ′$ ，点 $B$ 的对应点为点 $B ′$ .

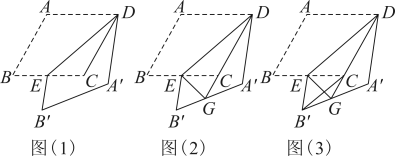(1)、【观察发现】 $A^{'} D$ 与 $B^{'} E$ 的位置关系是；

(2)、【思考表达】连接 $B^{'} C$ ，判断 $∠ D E C$ 与 $∠ B^{'} C E$ 是否相等，并说明理由；

(3)、如图（2），延长 $D C$ 交 $A^{'} B^{'}$ 于点 $G$ ，连接 $E G$ ，请探究 $∠ D E G$ 的度数，并说明理由；

(4)、【综合运用】如图（3），当 $∠ B = 60 °$ 时，连接 $B^{'} C$ ，延长 $D C$ 交 $A^{'} B^{'}$ 于点 $G$ ，连接 $E G$ ，请写出 $B^{'} C$ 、 $E G$ 、 $D G$ 之间的数量关系，并说明理由.

查看试题解析
5. 如图1，在矩形 $A B C D$ 中， $A B = 10$ ， $A D = 8$ ， $E$ 是 $A D$ 边上的一点，连接 $C E$ ，将矩形 $A B C D$ 沿 $C E$ 折叠，顶点 $D$ 恰好落在 $A B$ 边上的点 $F$ 处，延长 $C E$ 交 $B A$ 的延长线于点 $G$ ．

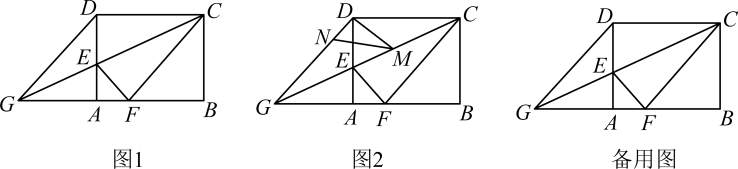(1)、求线段 $A E$ 的长；

(2)、求证四边形 $D G F C$ 为菱形；

(3)、如图2， $M$ ， $N$ 分别是线段 $C G$ ， $D G$ 上的动点（与端点不重合），且 $∠ D M N = ∠ D C M$ ，设 $D N = x$ ，是否存在这样的点 $N$ ，使 $△ D M N$ 是直角三角形？若存在，请求出 $x$ 的值；若不存在，请说明理由．

查看试题解析
6. 如图，平行四边形ABCD中，DB＝ $2 \sqrt{3}$ ， AB＝4，AD＝2，动点E，F同时从A点出发，点E沿着A→D→B的路线匀速运动，点F沿着A→B→D的路线匀速运动，当点E，F相遇时停止运动．

(1)、如图1，设点E的速度为1个单位每秒，点F的速度为4个单位每秒，当运动时间为 $\frac{2}{3}$ 秒时，设CE与DF交于点P，求线段EP与CP长度的比值；

(2)、如图2，设点E的速度为1个单位每秒，点F的速度为 $\sqrt{3}$ 个单位每秒，运动时间为x秒，ΔAEF的面积为y，求y关于x的函数解析式，并指出当x为何值时，y的值最大，最大值为多少？

(3)、如图3，H在线段AB上且AH＝ $\frac{1}{3}$ HB，M为DF的中点，当点E、F分别在线段AD、AB上运动时，探究点E、F在什么位置能使EM＝HM．并说明理由．

查看试题解析

二、模拟预测

7. 阅读下面的材料，并回答所提出的问题：如图所示，在锐角三角形 $A B C$ 中，求证： $\frac{b}{s i n B} = \frac{c}{s i n C}$
这个三角形不是一个直角三角形，不能直接使用锐角三角函数的知识去处理，所以必须构造直角三角形，过点A作 $A D ⊥ B C$ ，垂足为D，则在 $R t △ A B D$ 和 $R t △ A C D$ 中由正弦定义可完成证明．
解：如图，过点A作 $A D ⊥ B C ，$ ，垂足为D，
在 $R t △ A B D$ 中， $s i n B = \frac{A D}{A B}$ ，则 $A D = c s i n B$
$R t △ A C D$ 中， $s i n C = \frac{A D}{A C}$ ，则 $A D = b s i n C$
所以 $c s i n B = b s i n C$ ，即 $\frac{b}{s i n B} = \frac{c}{s i n C}$

(1)、在上述分析证明过程中，主要用到了下列三种数学思想方法的哪一种（　　）

A、数形结合的思想； B、转化的思想； C、分类的思想

(2)、用上述思想方法解答下面问题．
在 $△ A B C$ 中， $∠ C = 6 0^{°} ， A C = 6 ， B C = 8 ，$ ，求 $A B$ 和 $△ A B C$ 的面积．

(3)、用上述结论解答下面的问题（不必添加辅助线）
在锐角三角形 $A B C$ 中， $A C = 10 ， A B = 5 \sqrt{6} ， ∠ C = 60 °$ ，求 $∠ B$ 的度数．

查看试题解析
8. 在数学学习过程中，我们总是从一些最简单的图形出发，研究其中的边角关系，然后再应用所得到的结论去解决其他较复杂的问题．

(1)、【基本图形】如图（1），在 $△ A B C$ 中， $A B = A C = m$ ， $∠ B A C = α$ ，则 $B C =$ ．（用含m， $α$ 的式子表示）

(2)、【解决问题】在 $△ A B C$ 中， $A B = 10$ ， $∠ B A C = 45 °$ ， $∠ A B C = 60 °$ ．
①如图（2），P是 $B C$ 边上一动点，点P关于 $A B$ ， $A C$ 的对称点分别是D，E，连接 $A P$ ， $A D$ ， $A E$ ， $D E$ ，请写出 $A P$ 与 $D E$ 的数量关系，并说明理由；
②如图（3），若P，Q，R分别是边 $B C$ ， $A B$ ， $A C$ 上的动点，则 $△ P Q R$ 的周长的最小值为 ▲ ．

(3)、【应用拓展】如图（4），E，F分别是边长为 $2$ 的正方形 $A B C D$ 的边 $B C$ ， $D C$ 上的动点，且 $∠ E A F = 45 °$ ， P，Q，R分别是△ $A E F$ 的边 $A E$ ， $E F$ ， $A F$ 上的动点，请直接写出 $△ P Q R$ 的周长的最小值．

查看试题解析
9. 已知：⊙O是△ABC的外接圆，连接BO并延长交AC于点D，∠CDB＝3∠ABD.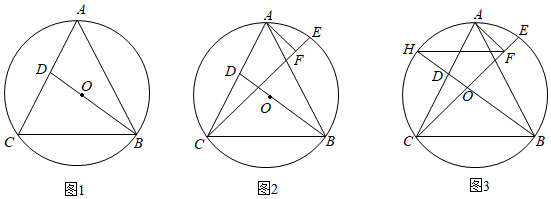

(1)、如图1，求证：AC＝AB；

(2)、如图2，点E是弧AB上一点，连接CE，AF⊥CE于点F，且∠BAF＝∠ACE，求tan∠BCE的值；

(3)、如图3，在（2）的条件下，延长BD交⊙O于点H，连接FH，若EF＝2，BC＝8 $\sqrt{2}$ ，求线段FH的长.

查看试题解析
10. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = α$ ，点D，E在线段 $A B$ 上 $(A D < A E)$ ，点F在 $C B$ 的延长线上，连接CD，EF， $∠ A C D = ∠ B E F$ ， $\frac{A C}{B C} = \frac{A D}{B F}$ ．

(1)、如图1，当 $α = 45 °$ 时，线段 $C D ， E F$ 的数量关系是；

(2)、如图2，当 $α = 30 °$ 时，请写出线段 $A C ， B E ， B F$ 的数量关系，并说明理由；

(3)、在（2）的条件下，当 $A B = 8$ ，点E是 $A B$ 中点时，请直接写出 $△ A D C$ 的面积．

查看试题解析
11. 如图

【问题提出】

正多边形内任意一点到各边距离之和与这个正多边形的半径 $R$ 和中心角有什么关系？

【问题探究】

如图①， $△ A B C$ 是等边三角形，半径 $O A = R$ ， $∠ A O B$ 是中心角， $P$ 是 $△ A B C$ 内任意一点， $P$ 到 $△ A B C$ 各边距离 $P F$ 、 $P E$ 、 $P D$ 分别为 $h_{1} 、 h_{2} 、 h_{3}$ ，设 $△ A B C$ 的边长是 $a$ ，面积为 $S$ ．过点 $O$ 作 $O M ⊥ A B$ ．

∴ $O M = R c o s \frac{1}{2} ∠ A O B = R c o s 60 °$ ， $A M = R s i n \frac{1}{2} ∠ A O B = R s i n 60 °$ ， $A B = 2 A M = 2 R s i n 60 °$ ，

∴ $S_{△ A B C} = 3 S_{△ A O B} = 3 \times \frac{1}{2} A B \times O M = 3 R^{2} s i n 60 ° c o s 60 °$ ， ①

∵ $S_{△ A B C}$ 又可以表示 $\frac{1}{2} a (h_{1} + h_{2} + h_{3})$ ②

联立①②得 $\frac{1}{2} a (h_{1} + h_{2} + h_{3}) = 3 R^{2} s i n 60 ° c o s 60 °$

∴ $\frac{1}{2} \times 2 R s i n 60 ° (h_{1} + h_{2} + h_{3}) = 3 R^{2} s i n 60 ° c o s 60 °$

∴ $h_{1} + h_{2} + h_{3} = 3 R c o s 60 °$

(1)、【问题解决】
如图②，五边形 $A B C D E$ 是正五边形，半径 $O A = R$ ， $∠ A O B$ 是中心角， $P$ 是五边形 $A B C D E$ 内任意一点， $P$ 到五边形 $A B C D E$ 各边距 $P H 、 P M 、 P N 、 P I 、 P L$ 分别为 $h_{1}$ 、 $h_{2}$ 、 $h_{3}$ 、 $h_{4}$ 、 $h_{5}$ ，参照（1）的分析过程，探究 $h_{1} + h_{2} + h_{3} + h_{4} + h_{5}$ 的值与正五边形 $A B C D E$ 的半径 $R$ 及中心角的关系．

(2)、【性质应用】
正六边形（半径是 $R$ ）内任意一点 $P$ 到各边距离之和 $h_{1} + h_{2} + h_{3} + h_{4} + h_{5} + h_{6} =$ ．

(3)、如图③，正 $n$ 边形（半径是 $R$ ）内任意一点 $P$ 到各边距离之和 $h_{1} + h_{2} + ⋯ + h_{n - 1} + h_{n} =$ ．

查看试题解析
12. 如图①，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 30 °$ ， $A C = 1$ ， D为 $A B$ 的中点， $E F$ 为 $△ A C D$ 的中位线，四边形 $E F G H$ 为 $△ A C D$ 的内接矩形（矩形的四个顶点均在 $△ A C D$ 的边上）.

(1)、计算矩形 $E F G H$ 的面积；

(2)、将矩形 $E F G H$ 沿 $A B$ 向右平移、点F落在 $B C$ 上时停止移动，在平移过程中，当矩形与 $△ C B D$ 重叠部分的面积为 $\frac{\sqrt{3}}{16}$ 时，求矩形平移的距离；

(3)、如图③，将（2）中矩形平移停止时所得的矩形记为矩形 $E_{1} F_{1} G_{1} H_{1}$ ，将矩形 $E_{1} F_{1} G_{1} H_{1}$ 绕 $G_{1}$ 点按顺时针方向旋转，当H₁落在 $C D$ 上时停止转动，旋转后的矩形记为矩形 $E_{2} F_{2} G_{2} H_{2}$ ，设旋转角为 $α$ ，求 $c o s α$ 的值.

查看试题解析
13.

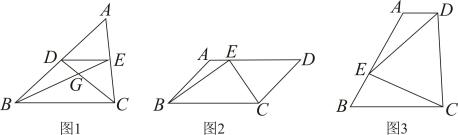(1)、问题提出：如图1，在 $△ A B C$ 中，点 $D$ 、 $E$ 分别是 $A B$ 、 $A C$ 的中点，连接 $D E$ 、 $C D$ 、 $B E$ ， $C D$ 与 $B E$ 交于点 $G$ ，若 $S_{△ D E G} = 2$ ，则 $S_{△ B C G} =$ ；

(2)、问题探究：如图2，在 $▱ A B C D$ 中， $A B = 2$ ， $∠ D = 45 °$ ，点 $E$ 是 $A D$ 上一点（可与端点重合），连接 $B E$ 、 $C E$ ， $B E ⊥ C E$ ，求 $▱ A B C D$ 面积的最小值；

(3)、问题解决：某湿地公园拟建一个梯形花园 $A B C D$ ，示意图如图3所示，其中 $A D ∥ B C$ ， $A B = 60 \sqrt{3} m$ ， $∠ A B C = 60 °$ .管理员计划在 $△ A D E$ 区域种植水生植物，在 $△ A D E$ 区域种植甲种花卉.根据设计要求，要满足点 $E$ 在 $A B$ 上， $A E = 2 B E$ ， $∠ D E C$ 是锐角，且 $t a n ∠ D E C = 2$ ，若种植水生植物每平方米需400元，种植甲种花卉每平方米需100元，求种植水生植物和种植甲种花卉所需总费用至少为多少元？

查看试题解析
14. 综合与实践
问题背景：
在综合与实践课上，老师让同学们探索有一组邻边相等，一组对角互补的四边形的性质．如图1，在四边形 $A B C D$ 中， $D A = D C$ ， $∠ A B C + ∠ A D C = 180 °$ ．

(1)、实践操作：
同学们首先从特殊情形开始探索，如图2，当 $∠ A B C = 90 °$ 时，其它条件不变，发现了 $B D$ 平分 $∠ A B C$ 的性质，有两个小组给出如下的证明思路：
“团结组”：利用“在一个角的内部，到角的两边距离相等的点在这个角的平分线上”；
“实践组”：由 $D A = D C$ 想到将 $△ A B D$ 绕点 $D$ 旋转，使 $D A$ 与 $D C$ 重合，将四边形 $A B C D$ 转化成我们学过的特殊图形．
①请你分别在图2，图3中画出符合“团结组”和“实践组”思路的辅助线；
②求证： $B D$ 平分 $∠ A B C$ ；（从上面的两个思路中选一个或按照自己的思路）

(2)、“创新组”的同学发现在图2中 $A B + B C = \sqrt{2} B D$ ，请你说明理由；

(3)、拓展延伸：
“善思组”的同学受“创新组”同学的启发，提出如下问题：如图4，当 $∠ A B C = 120 °$ 时，其它条件不变，延长 $B D$ 到点 $F$ ，使 $\frac{D F}{B D} = \frac{1}{4}$ ，过点 $F$ 分别作 $F G ∥ C B$ 交 $B A$ 的延长线于点 $G$ ， $F E ∥ A B$ 交 $B C$ 的延长线于点 $E$ ，若 $G F = 5 \sqrt{3}$ ，则四边形 $B E F G$ 的形状为，四边形 $A B C D$ 的面积为．

查看试题解析
15. 在半径为10的扇形AOB中， $∠ A O B = 90 °$ ，延长OB到点C，使 $B C = O B = 10$ ．点D为 $\overset{⌢}{A B}$ 上的动点，点E是扇形所在平面内的点，连接OD，DE，EC，当 $D E = E C = 10$ 时，解答下列问题：

(1)、论证：如图1，连接OE，DC，当 $O D ∥ E C$ 时，求证： $O E = D C$ ；

(2)、发现：当 $∠ D O C = 60 °$ 时，∠ODE的度数可能是多少？

(3)、尝试：如图2，当点D，E，C三点共线时，求点D到OA所在直线的距离；

(4)、拓展：当点E在OC的下方，且DE与 $\overset{⌢}{A B}$ 相切时，直接写出∠DOC的余弦值．

查看试题解析