备考2023年中考数学压轴题训练 ——四边形(3)
试卷更新日期:2023-05-14 类型:三轮冲刺
一、真题
-
1.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证:
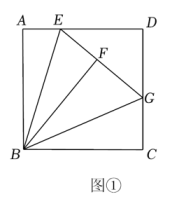 (2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长. (3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长.
(3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长. 2. 如图,在菱形ABCD中,∠BAD = 120°,AB = 6,连接BD .
2. 如图,在菱形ABCD中,∠BAD = 120°,AB = 6,连接BD . (1)、求BD的长;(2)、点E为线段BD上一动点(不与点B,D重合), 点F在边AD上,且BE=DF,
(1)、求BD的长;(2)、点E为线段BD上一动点(不与点B,D重合), 点F在边AD上,且BE=DF,①当CE丄AB时,求四边形ABEF的面积;
②当四边形ABEF的面积取得最小值时,CE+CF的值是否也最小?如果是,求CE+CF的最小值;如果不是,请说明理由.
3. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .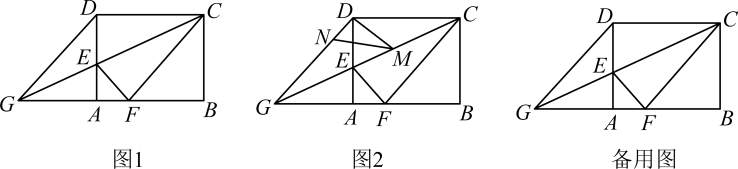 (1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.4. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;
(1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.4. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;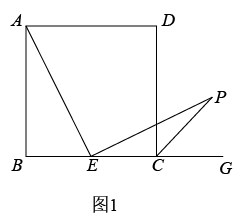
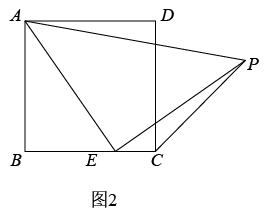
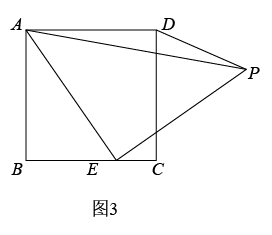 (1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.
(1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.二、模拟预测
-
5. 定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.

根据以上定义,解决下列问题:
(1)、如图1,正方形ABCD中E是CD上的点,将△BCE绕B点旋转,使BC与BA重合,此时点E的对应点F在DA的延长线上,则四边形BEDF (填“是”或“不是”)“直等补”四边形;(2)、如图2,已知四边形ABCD是“直等补”四边形,AB=BC=10,CD=2,AD>AB,过点B作BE⊥AD于E.①过C作CF⊥BF于点F,试证明:BE=DE,并求BE的长;
②若M是AD边上的动点,求△BCM周长的最小值.
6.(1)、【问题探究】如图1,在正方形中,点E、F分别在边、上,且 , 求证:. (2)、【知识迁移】如图2,在矩形中, , , 点E在边上,点M、N分别在边、上,且 , 求的值.
(2)、【知识迁移】如图2,在矩形中, , , 点E在边上,点M、N分别在边、上,且 , 求的值. (3)、【拓展应用】如图3,在平行四边形中, , , 点分别在边上,点M、N分别在边、上,当与的度数之间满足什么数量关系时,有?试写出其数量关系,并说明理由.
(3)、【拓展应用】如图3,在平行四边形中, , , 点分别在边上,点M、N分别在边、上,当与的度数之间满足什么数量关系时,有?试写出其数量关系,并说明理由. 7. 平行四边形中,点E在边上,连 , 点F在线段上,连 , 连 .
7. 平行四边形中,点E在边上,连 , 点F在线段上,连 , 连 . (1)、如图1,已知 , 点E为中点, . 若 , 求的长度;(2)、如图2,已知 , 将射线沿翻折交于H,过点C作交于点G.若 , 求证:;(3)、如图3,已知 , 若 , 直接写出的最小值.8. 将正方形的边绕点A逆时针旋转至 , 记旋转角为 , 连接 , 过点B作直线 , 垂足为点F,连接 .
(1)、如图1,已知 , 点E为中点, . 若 , 求的长度;(2)、如图2,已知 , 将射线沿翻折交于H,过点C作交于点G.若 , 求证:;(3)、如图3,已知 , 若 , 直接写出的最小值.8. 将正方形的边绕点A逆时针旋转至 , 记旋转角为 , 连接 , 过点B作直线 , 垂足为点F,连接 . (1)、如图1,当时,的形状为 , 的值为;(2)、当时,
(1)、如图1,当时,的形状为 , 的值为;(2)、当时,①(1)中的两个结论是否仍然成立?如果成立,请根据图2的情形进行证明;如果不成立,请说明理由;
②如图3,正方形边长为4, , , 在旋转的过程中,是否存在与相似?若存在,则的值为 ▲ , 若不存在,请说明理由.
9. 在正方形中,点是对角线上的动点(与点 , 不重合),连接 . (1)、将射线绕点顺时针旋转 , 交直线于点 .
(1)、将射线绕点顺时针旋转 , 交直线于点 .①依题意补全图1;
②小深通过观察、实验,发现线段存在以下数量关系:的平方和等于的平方.小深把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
想法1:将线段绕点逆时针旋转 , 得到线段 , 要证的关系,只需证的关系.
想法2:将沿翻折,得到 , 要证的关系,只需证的关系.
…
请你参考上面的想法,用等式表示线段的数量关系并证明;(一种方法即可)
(2)、如图2,若将直线绕点B顺时针旋转 , 交直线于点 . 若正方形边长为 , , 求的长.10. 综合与实践问题情境:数学活动课上,老师出示了一个问题:如图①,在中, , 垂足为E,F为的中点,连接 , , 试猜想与的数量关系,并加以证明.


 (1)、独立思考:请解答老师提出的问题;(2)、实践探究:希望小组受此问题的启发,将沿着(F为的中点)所在直线折叠,如图②,点C的对应点为 , 连接并延长交于点G,请判断与的数量关系,并加以证明.(3)、问题解决:智慧小组突发奇想,将沿过点B的直线折叠,如图③,点A的对应点为 , 使于点H,折痕交于点M,连接 , 交于点N.该小组提出一个问题:若此的面积为20,边长 , , 求图中阴影部分(四边形)的面积.请你思考此问题,直接写出结果.11. 如图1,已知点G在正方形的对角线上, , 垂足为点E, , 垂足为点F.
(1)、独立思考:请解答老师提出的问题;(2)、实践探究:希望小组受此问题的启发,将沿着(F为的中点)所在直线折叠,如图②,点C的对应点为 , 连接并延长交于点G,请判断与的数量关系,并加以证明.(3)、问题解决:智慧小组突发奇想,将沿过点B的直线折叠,如图③,点A的对应点为 , 使于点H,折痕交于点M,连接 , 交于点N.该小组提出一个问题:若此的面积为20,边长 , , 求图中阴影部分(四边形)的面积.请你思考此问题,直接写出结果.11. 如图1,已知点G在正方形的对角线上, , 垂足为点E, , 垂足为点F.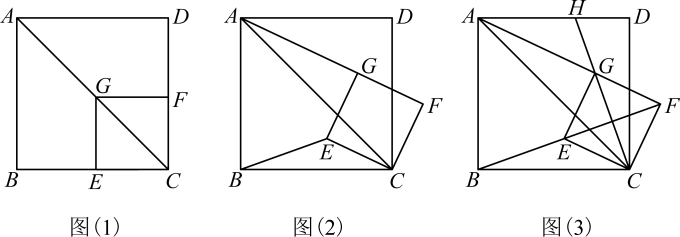 (1)、证明与推断:
(1)、证明与推断:②求证:四边形是正方形;
②推断:的值为 ▲ ;
(2)、探究与证明:将正方形的绕点C顺时针方向旋转 , 如图2所示,试探究线段与之间的数量关系,并说明理由;
(3)、拓展与运用:正方形在旋转过程中,当B、E、F三点在一条直线上时,如图3所示,延长交于点H,若 , 则 .
12. 数学学习总是循序渐进、不断延伸拓展的,数学知识往往起源于人们为了解决某些问题,通过观察、测量、思考、猜想出的一些结论.但是所猜想的结论不一定都是正确的.人们从已有的知识出发,经过推理、论证后,如果所猜想的结论在逻辑上没有矛盾,就可以作为新的推理的前提,数学中称之为定理. (1)、推理证明:
(1)、推理证明:在八年级学习等腰三角形和直角三角形时,借助工具测量就能够发现:“直角三角形斜边上的中线等于斜边的一半”,当时并未说明这个结论的符合题意性.九年级学习了矩形的判定和性质之后,就可以解决这个问题了.如图1,在中,若是斜边上的中线,则 , 请你用矩形的性质证明这个结论的符合题意性.
(2)、迁移运用:利用上述结论解决下列问题:①如图2,在线段异侧以为斜边分别构造两个直角三角形与 , E、F分别是、的中点,判断与的位置关系并说明理由;
②如图3,对角线、相交于点O,分别以、为斜边且在同侧分别构造两个直角三角形与 , 求证:是矩形;
13. (1)、【操作体验】用一张矩形纸片折等边三角形.
(1)、【操作体验】用一张矩形纸片折等边三角形.第一步,对折矩形纸片()(图),使与重合,得到折痕 , 把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点C落在上的P处,并使折痕经过点B,得到折痕 , 折出 , , 得到 .
请证明△PBC是等边三角形.
(2)、【数学思考】如图④,小明画出了图③的矩形和等边三角形 . 他发现,在矩形中把经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.
(3)、【问题解决】已知矩形一边长为 , 另一边长为 . 对于每一个确定的的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的的取值范围.
14. 如图1,在正方形ABCD中,E为边AD上的一点,连结CE,过D作DF⊥CE于点G,DF交边AB于点F.已知DG=4,CG=16. (1)、EG的长度是 .(2)、如图2,以G为圆心,GD为半径的圆与线段DF、CE分别交于M、N两点.
(1)、EG的长度是 .(2)、如图2,以G为圆心,GD为半径的圆与线段DF、CE分别交于M、N两点.①连接CM、BM,若点P为BM的中点,连结CP,求证∠BCP=∠MCP.
②连接CN、BN,若点Q为BN的中点,连结CQ,求线段CQ的长.
15. 如图 (1)、动手操作:如图1,将一张长方形的纸对折两次,然后沿45°的方向剪下一个角,打开,剪出的是一个形.再利用图形的“旋转”开展数学探究活动,体会图形在旋转过程中的变化及其蕴含的数学思想方法;(2)、问题探究:如图2,由“动手操作”所得的四边形的对角线相交于点 , 把一个与它全等的四边形绕点旋转,交于 , 交于 . 探究线段 , 之间的数量关系,并说明理由;(3)、拓展迁移:如图3,矩形的对角线交点为 , 直角的边 , 分别与边 , 相交于 , . 设(为常数),探究线段 , 之间的数量关系,并说明理由.16. 如图
(1)、动手操作:如图1,将一张长方形的纸对折两次,然后沿45°的方向剪下一个角,打开,剪出的是一个形.再利用图形的“旋转”开展数学探究活动,体会图形在旋转过程中的变化及其蕴含的数学思想方法;(2)、问题探究:如图2,由“动手操作”所得的四边形的对角线相交于点 , 把一个与它全等的四边形绕点旋转,交于 , 交于 . 探究线段 , 之间的数量关系,并说明理由;(3)、拓展迁移:如图3,矩形的对角线交点为 , 直角的边 , 分别与边 , 相交于 , . 设(为常数),探究线段 , 之间的数量关系,并说明理由.16. 如图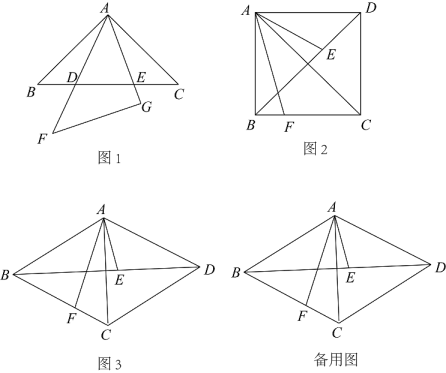 (1)、【教材呈现】如图1,在同一平面内,将两个全等的等腰直角三角形和摆放在一起,点为公共顶点, , 若固定不动,将绕点旋转,边 , 与边分别交于点 , (点不与点重合,点不与点重合),则结论是否成立(填“成立”或“不成立”);(2)、【类比引申】如图2,在正方形中,为内的一个动角,两边分别与 , 交于点 , , 且满足 , 求证:;(3)、【拓展延伸】如图3,菱形的边长为 , , 的两边分别与 , 相交于点 , , 且满足 , 若 , 则线段的长为 .17. 如图,已知矩形中, , , 点 , 分别在边 , 上,沿着折叠矩形 , 使点 , 分别落在 , 处,且点在线段上(不与两端点重合),过点作于点 , 连接 .
(1)、【教材呈现】如图1,在同一平面内,将两个全等的等腰直角三角形和摆放在一起,点为公共顶点, , 若固定不动,将绕点旋转,边 , 与边分别交于点 , (点不与点重合,点不与点重合),则结论是否成立(填“成立”或“不成立”);(2)、【类比引申】如图2,在正方形中,为内的一个动角,两边分别与 , 交于点 , , 且满足 , 求证:;(3)、【拓展延伸】如图3,菱形的边长为 , , 的两边分别与 , 相交于点 , , 且满足 , 若 , 则线段的长为 .17. 如图,已知矩形中, , , 点 , 分别在边 , 上,沿着折叠矩形 , 使点 , 分别落在 , 处,且点在线段上(不与两端点重合),过点作于点 , 连接 .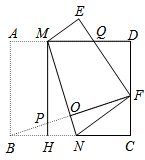 (1)、求证:;(2)、若 , 求的长;(3)、若 , 求折叠后重叠部分的面积.
(1)、求证:;(2)、若 , 求的长;(3)、若 , 求折叠后重叠部分的面积.