备考2023年中考数学压轴题训练 ——四边形（1）

试卷更新日期：2023-05-14 类型：三轮冲刺

进入出卷网下载

一、真题

1. 同学们还记得吗？图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形．受这两个图形的启发，数学兴趣小组提出了以下三个问题，请你回答：

(1)、【问题一】如图①，正方形 $A B C D$ 的对角线相交于点 $O$ ，点 $O$ 又是正方形 $A_{1} B_{1} C_{1} O$ 的一个顶点， $O A_{1}$ 交 $A B$ 于点 $E$ ， $O C_{1}$ 交 $B C$ 于点 $F$ ，则 $A E$ 与 $B F$ 的数量关系为；

(2)、【问题二】受图①启发，兴趣小组画出了图③：直线 $m$ 、 $n$ 经过正方形 $A B C D$ 的对称中心 $O$ ，直线 $m$ 分别与 $A D$ 、 $B C$ 交于点 $E$ 、 $F$ ，直线 $n$ 分别与 $A B$ 、 $C D$ 交于点 $G$ 、 $H$ ，且 $m ⊥ n$ ，若正方形 $A B C D$ 边长为8，求四边形 $O E A G$ 的面积；

(3)、【问题三】受图②启发，兴趣小组画出了图④：正方形 $C E F G$ 的顶点 $G$ 在正方形 $A B C D$ 的边 $C D$ 上，顶点 $E$ 在 $B C$ 的延长线上，且 $B C = 6$ ， $C E = 2$ ．在直线 $B E$ 上是否存在点 $P$ ，使 $△ A P F$ 为直角三角形？若存在，求出 $B P$ 的长度；若不存在，说明理由．

查看试题解析
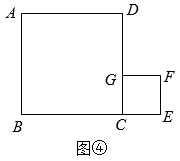2. 如图，在平面直角坐标系中，平行四边形ABCD的边AB在x轴上，顶点D在y轴的正半轴上，M为BC的中点，OA、OB的长分别是一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两个根 $(O A < O B)$ ， $t a n ∠ D A B = \frac{4}{3}$ ，动点P从点D出发以每秒1个单位长度的速度沿折线 $D C - C B$ 向点B运动，到达B点停止．设运动时间为t秒， $△ A P C$ 的面积为S．

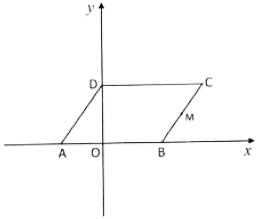(1)、求点C的坐标；

(2)、求S关于t的函数关系式，并写出自变量t的取值范围；

(3)、在点P的运动过程中，是否存在点P，使 $△ C M P$ 是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析
3. 平行四边形 $A B C D$ ，若 $P$ 为 $B C$ 中点， $A P$ 交 $B D$ 于点 $E$ ，连接 $C E$ ．

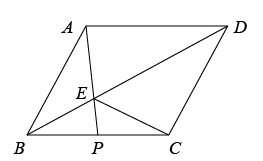(1)、若 $A E = C E$ ，
①证明 $A B C D$ 为菱形；

②若 $A B = 5$ ， $A E = 3$ ，求 $B D$ 的长．

(2)、以 $A$ 为圆心， $A E$ 为半径， $B$ 为圆心， $B E$ 为半径作圆，两圆另一交点记为点 $F$ ，且 $C E = \sqrt{2} A E$ ．若 $F$ 在直线 $C E$ 上，求 $\frac{A B}{B C}$ 的值．

查看试题解析
4. 如图，在菱形ABCD中，AB=5，BD为对角线.点E是边AB延长线上的任意一点，连结DE交BC于点F，BG平分∠CBE交DE于点G．

(1)、求证： $∠ D B G = 90 °$ .

(2)、若 $B D = 6 ， D G = 2 G E$ ．
①求菱形 $A B C D$ 的面积.

②求 $\tan ∠ B D E$ 的值.

(3)、若 $B E = A B$ ，当 $∠ D A B$ 的大小发生变化时（ $0 ° < ∠ D A B < 180 °$ ），在AE上找一点T，使GT为定值，说明理由并求出ET的值．

查看试题解析
5. 如图，在矩形 ABCD中，AB=6，BC=8，动点 E从点A出发，沿边AD，DC向点C运动，A， D关于直线 BE的对称点分别为M，N，连结MN ．

(1)、如图，当E在边AD上且 DE=2时，求 ∠AEM的度数．

(2)、当N在BC延长线上时，求DE的长，并判断直线MN与直线BD的位置关系，说明理由．

(3)、当直线MN恰好经过点 C 时，求DE的长．

查看试题解析
6. 在正方形ABCD中，点M是边AB的中点，点E在线段AM上（不与点A重合），点F在边BC上，且AE=2BF，连接EF，以EF为边在正方形ABCD内作正方形EFGH．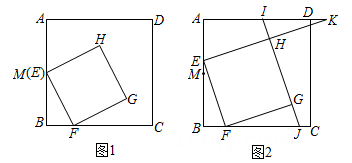

(1)、如图1．若AB=4，当点E与点M重合时，求正方形EFGH的面积

(2)、如图2．已知直线HG分别与边AD，BC交于点I，J，射线EH与射线AD交于点K．
①求证：EK=2EH；

②设∠AEK=α，△FGJ和四边形AEHI的面积分别为S₁、S₂ ．

求证： $\frac{S_{2}}{S_{1}}$ =4sin²α-1．

查看试题解析
7. 如图，在菱形ABCD中，AB=10. $\sin B = \frac{3}{5}$ ，点E从点B出发沿折线B-C-D向终点D运动.过点E作点E所在的边(BC或CD)的垂线，交菱形其它的边于点F，在EF的右侧作矩形EFGH.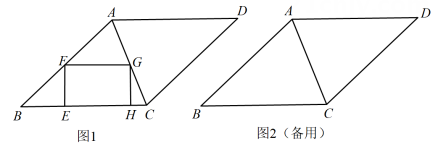

(1)、如图1，点G在AC上.求证：FA=FG.

(2)、若EF=FG，当EF过AC中点时，求AG的长.

(3)、已知FG=8，设点E的运动路程为s.当s满足什么条件时，以G，C，H为顶点的三角形与△BEF相似(包括全等)？

查看试题解析

二、模拟预测

8. 在矩形 $A B C D$ 中， $A B = 8$ ， $B C = 6$ ，将矩形 $A B C D$ 绕点B顺时针旋转得到矩形 $A_{1} B C_{1} D_{1}$ ， A，C，D的对应点分别为 $A_{1}$ ， $C_{1}$ ， $D_{1}$ ．

(1)、当点 $A_{1}$ 落在线段 $D C$ 上时，完成以下探究．
①如图1，求 $D A_{1}$ 的长．
②如图2，延长 $D C$ 交 $C_{1} D_{1}$ 于点E，求证： $△ B C A_{1} ≌ △ A_{1} D_{1} E$ ．

(2)、如图3，以 $B C$ 为斜边在右侧作等腰直角三角形 $B C F$ ， $∠ F = 9 0^{∘}$ ， $C F$ 交 $B C_{1}$ 于点G，交 $C_{1} D_{1}$ 于点H，若 $G F = \sqrt{7}$ ，求 $D_{1} H$ 的长．

(3)、如图4，矩形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点P，连接 $P A_{1}$ ， $P D_{1}$ ，则 $△ P A_{1} D_{1}$ 面积的最小值为．

查看试题解析
9. 如图

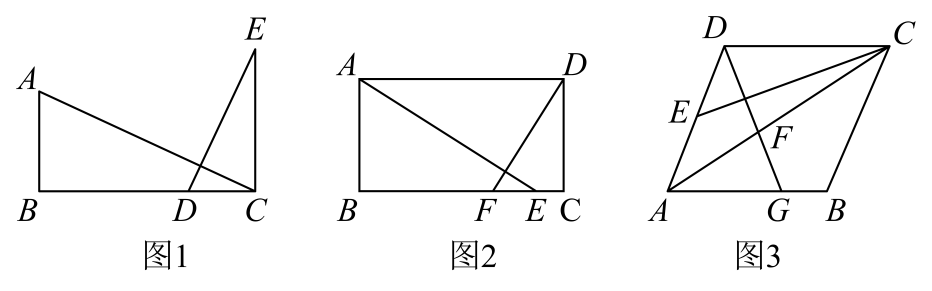(1)、【基础巩固】
如图1， $A B ⊥ B C$ 于点B， $C E ⊥ B C$ 于点C， $A C ⊥ D E$ 交BC于点D，求证： $\frac{A C}{D E} = \frac{B C}{C E}$ 。

(2)、【尝试应用】
如图2，在矩形ABCD中，E是BC上的一点，作 $D F ⊥ A E$ 交BC于点F， $C E = E F$ ，若 $A B = 2$ ， $A D = 4$ ，求 $\frac{A E}{D F}$ 的值。

(3)、【拓展提高】
如图，菱形ABCD的边长为10， $t a n ∠ A C D = \frac{3}{4}$ ， E为AD上的一点，作 $D G ⊥ C E$ 交AC于点F，交AB于点G，且 $C E = 2 D F$ ，求BG的长。

查看试题解析
10. 如图1和图2，在四边形 $A B C D$ 中， $A B = C D = 6$ ， $A D = 2$ ， $B C = 8$ ， $∠ B = ∠ C = 60 °$ ，点K在 $C D$ 边上，点M，N分别在 $A B$ ， $B C$ 边上，且 $A M = C N = 2$ ，点P从点M出发沿折线 $M B - B N$ 匀速运动，点E在 $C D$ 边所在直线上随P移动，且始终保持 $∠ M P E = ∠ B$ ；点Q从点D出发沿 $D C$ 匀速运动，点P，Q同时出发，点Q的速度是点P的一半，点P到达点N停止，点Q随之停止．设点P移动的路程为x．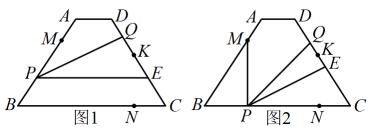

(1)、当 $x = 5$ 时，求 $P N$ 的长；

(2)、当 $M P ⊥ B C$ 时，求x的值；

(3)、用含x的式子表示 $Q E$ 的长；

(4)、已知点P从点M到点B再到点N共用时20秒，若 $C K = \frac{15}{4}$ ，请直接写出点K在线段 $Q E$ 上（包括端点）的总时长．

查看试题解析
11. 如图1，正方形 $A F E G$ 与正方形 $A B C D$ 有公共点 $A$ ，点 $G$ ， $F$ 分别在 $A D$ ， $A B$ 上，点 $E$ 在正方形 $A B C D$ 的对角线 $A C$ 上．将正方形 $A F E G$ 绕 $A$ 点逆时针方向旋转，旋转角为 $α$ （ $0 ° \leq α \leq 360 °$ ）．

(1)、当 $α = 0 °$ 时， $\frac{C E}{D G} =$ ；

(2)、如图2，当 $0 ° < α < 45 °$ 时，连接 $C E$ ， $D G$ ， $\frac{C E}{D G}$ 是否为定值？请说明理由；

(3)、若 $A B = 2 \sqrt{2}$ ， $A G = 2$ ，当 $C$ ， $G$ ， $E$ 三点共线时，求 $D G$ 的长度．

查看试题解析
12. 综合与实践
问题情境
如图1，已知线段 $A B = 6$ ，射线 $A M ⊥ A B$ ，射线 $B N ⊥ A B$ ，点D在射线 $A M$ 上沿着 $A M$ 的方向运动，过点D作 $D C ⊥ A M$ 交 $B N$ 于点C，点E是 $A D$ 的中点，连接 $B E$ ，将 $△ A B E$ 沿着BE折叠，点A的对应点为点F，连接 $A F ， C F$ ．

(1)、探究展示：当 $∠ A B E = 30 °$ 时，求 $\frac{C F^{2}}{A F^{2}}$ 的值；

(2)、如图2，延长 $A F$ 交 $D C$ 于点G，当点G恰好是 $D C$ 中点时，求证：四边形 $A B C D$ 是正方形；

(3)、拓展探究：在图2中，若 $A B = A D$ ，直接写出 $C F$ 的长度．

查看试题解析
13.

(1)、问题提出
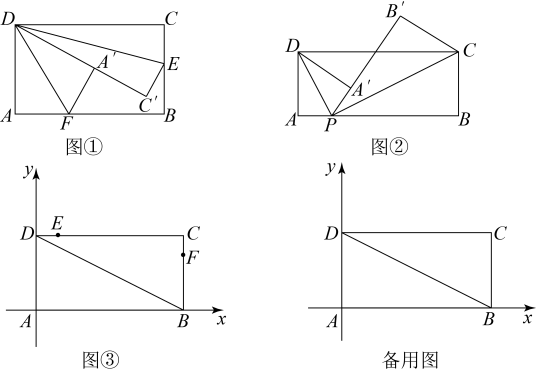
如图①，在矩形 $A B C D$ 的边 $B C$ 上找一点E，将矩形沿直线 $D E$ 折叠，点C的对应点为 $C^{'}$ ，再在 $A B$ 上找一点F，将矩形沿直线 $D F$ 折叠，使点A的对应点 $A^{'}$ 落在 $D C$ 上则 $∠ E D F =$ ．

(2)、问题探究
如图②在矩形 $A B C D$ 中， $A B = 10$ ， $A D = 4$ ，点P是矩形 $A B C D$ 边 $A B$ 上一点，连接 $P D 、 P C$ ，将 $△ A D P$ 、 $△ B C P$ 分别沿 $P D 、 P C$ 翻折，得到 $△ A^{'} D P$ 、 $△ B^{'} P C$ ，当P、 $A^{'}$ 、 $B^{'}$ 三点共线时，则称P为 $B C$ 边上的“优叠点”，求此时 $A P$ 的长度．

(3)、问题解决
如图③，矩形 $A B C D$ 位于平面直角坐标系中， $A D = 4$ ， $A D < A B$ ．点A在标原点，B，D分别在x轴与y轴上，点E和点F分别是 $C D$ 和 $B C$ 边上的动点，运动过程中始终保持 $D E + B F = 4$ ．当点P是 $A B$ 边上唯一的“优叠点”时，连接 $P E$ 交 $B D$ 于点M，连接 $P F$ 交 $B D$ 于点N，请问 $D M + B N$ 是否能取得最大值？如果能，请确定此时点M的位置（即求出点M的坐标）及四边形 $A D E P$ 的面积，若不能，请说明理由．

查看试题解析
14. 如图， $B D$ 是 $▱ A B C D$ 的对角线， $A B ⊥ B D$ ， $B D = 8 c m$ ， $A D = 10 c m$ ．动点 $P$ 从点 $D$ 出发，以 $5 c m / s$ 的速度沿 $D A$ 运动到终点 $A$ ，同时动点 $Q$ 从点 $B$ 出发，沿折线 $B D -$ $D C$ 运动到终点 $C$ ，在 $B D$ 、 $D C$ 上分别以 $8 c m / s$ 、 $6 c m / s$ 的速度运动，过点 $Q$ 作 $Q M ⊥ A B$ ，交射线 $A B$ 于点 $M$ ，连结 $P Q$ ；以 $P Q$ 与 $Q M$ 为边作 $▱ P Q M N$ ，设点 $P$ 的运动时间为 $t (s) (t > 0)$ ， $▱ P Q M N$ 与 $▱ A B C D$ 重叠部分图形的面积为 $S (c m^{2})$ ．

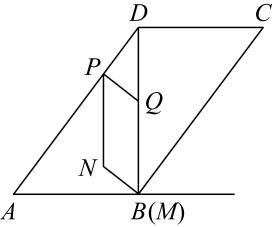(1)、 $A P =$ $c m$ （用含 $t$ 的代数式表示）．

(2)、当点 $N$ 落在边 $A B$ 上时，求 $t$ 的值．

(3)、当点 $Q$ 在线段 $D C$ 上运动时， $t$ 为何值时， $S$ 有最大值？最大值是多少？

(4)、连结 $N Q$ ，当 $N Q$ 与 $△ A B D$ 的一边平行时，直接写出 $t$ 的值．

查看试题解析
15. 在平面直角坐标系中，点O为坐标原点，直线 $y = k x + 6 k (k \neq 0)$ 与x轴交于点A，四边形 $O A B C$ 是平行四边形， $B C$ 边与y轴交于点E．

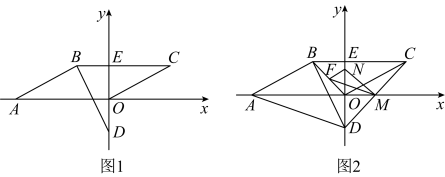(1)、求点A的坐标；

(2)、如图1，过B作 $A B$ 的垂线交y轴负半轴于点D， $E C = E D$ ，设点B的横坐标为t， $O D$ 长为d，求d与t的函数关系式（不要求写出自变量t的取值范围）；

(3)、如图2，在（2）的条件下，连接 $A D 、 O B 、 C D$ ，当以 $C D ， O B ， A D$ 的长为三边长构成的三角形面积是8时，在 $O B$ 上取中点F，在 $O E$ 上取点N，将射线 $F N$ 绕点F顺时针旋转 $45 °$ 交x轴正半轴于点M，连接 $M N$ ，若 $△ O M N$ 的周长为6，直线 $y = k x + 6 k$ 经过点N，求k的值．

查看试题解析
16. 如图1，在矩形 $A B C D$ 中， $A B = 4$ ， $∠ A C B = 30 °$ .P，Q分别是 $A C$ ， $C D$ 上的动点，且满足 $\frac{D Q}{C P} = \frac{3}{5}$ ， E是射线 $A D$ 上一点， $A P = E P$ ，设 $D Q = x$ ， $A P = y$ .

(1)、求y关于x的函数表达式.

(2)、当 $△ P Q E$ 中有一条边与 $A C$ 垂直时，求 $D Q$ 的长.

(3)、如图2，当点Q运动到点C时，点P运动到点F.连结 $F Q$ ，以 $F Q$ ， $P Q$ 为边作 $▱ P Q F G$ .
①当 $G F$ 所在直线经过点D时，求 $▱ P Q F G$ 的面积；
②当点G在 $△ A B C$ 的内部（不含边界）时，直接写出x的取值范围.

查看试题解析
17. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， A C = 8 ， B C = 6$ ，点P从点C出发，以每秒2个单位长度的速度沿 $C A$ 方向向点A运动，同时，点Q从点B出发，以每秒1个单位长度的速度沿 $B C$ 方向向点C运动.当一个点到达终点时，另一个点也随之停止运动.连接 $P Q$ ，在射线 $P C$ 上截取 $P M = P Q$ ，以 $P Q ， P M$ 为邻边作菱形 $P Q N M$ ，设运动时间为t秒 $(t > 0)$ .

(1)、当 $t = 3$ 时，求菱形 $P Q N M$ 的面积.

(2)、当 $△ P C Q$ 的面积为菱形 $P Q N M$ 面积的 $\frac{1}{4}$ 时，求t的值.

(3)、作点B关于直线 $P Q$ 的对称点 $B^{'}$ .
①当 $∠ B Q B^{'} = 2 ∠ A B C$ 时，求线段 $B B^{'}$ 的长.
②当点 $B^{'}$ 落在菱形 $P Q N M$ 的边上时，请直接写出 $\frac{C Q}{B B^{'}}$ 的值.

查看试题解析
18. 如图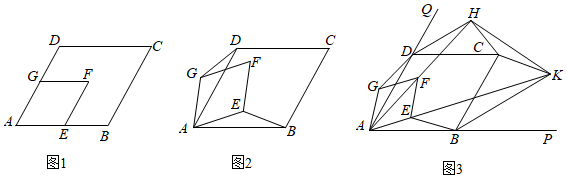

【证明体验】

如图1，四边形 $ABCD$ 和四边形 $AEFG$ 都是菱形， $∠ DAB = ∠ GAE = 60 °$ ，点 $G$ ，点 $E$ 分别在边 $AD$ ， $AB$ 上，点 $F$ 在菱形 $ABCD$ 内部，将菱形 $AEFG$ 绕点 $A$ 旋转一定的角度 $α$ ，点 $E$ ， $F$ 始终在菱形 $ABCD$ 的内部.

(1)、图2，求证： $△ DGA$ ≌ $△ BEA$ .

(2)、【思考探究】
如图3，点 $P$ ， $Q$ 分别在 $AB$ ， $AD$ 延长线上，连接 $AF$ 并延长与 $∠ QDC$ 的平分线交于点 $H$ ，连接 $AE$ 并延长与 $∠ PBC$ 的平分线交于 $K .$ 连接 $DH$ ， $HK$ ， $CH$ ， $CK$ .
$①$ 求证： $△ ADH$ ∽ $△ KBA$ ；

$②$ 若 $AB = 2 \sqrt{10}$ ， $DH = 5$ ，则线段 $BK$ 的长度为▲ ，线段 $HK$ 的长为▲ .

$③$ 菱形 $AEFG$ 绕点 $A$ 旋转 $α$ 度 $(0 ° < α < 30 °)$ ， $AB = m$ ， $△ KBC$ 是等腰三角形，线段 $HK$ 的长为.

查看试题解析
19. 如图1，菱形 $ABCD$ 的边长为 $12 cm$ ， $∠ B = 60 °$ ， $M$ ， $N$ 分别在边 $AB$ ， $CD .$ 上， $AM = 3 cm$ ， $DN = 4 cm$ ，点 $P$ 从点 $M$ 出发，沿折线 $MB - BC$ 以 $1 cm / s$ 的速度向点 $C$ 匀速运动 $($ 不与点 C重合 $)$ ； $△ APC$ 的外接圆 $⊙ O$ 与 $CD$ 相交于点 $E$ ，连接 $PE$ 交 $AC$ 于点 $F .$ 设点 $P$ 的运动时间为ts.

(1)、 $∠ APE =$ $°$ ；

(2)、若 $⊙ O$ 与 $AD$ 相切，
$①$ 判断 $⊙ O$ 与 $CD$ 的位置关系；

$②$ 求 $\overset{⌢}{APC}$ 的长；

(3)、如图3，当点 $P$ 在 $BC$ 上运动时，求 $CF$ 的最大值，并判断此时 $PE$ 与 $AC$ 的位置关系；

(4)、若点 $N$ 在 $⊙ O$ 的内部，直接写出 $t$ 的取值范围.

查看试题解析