备考2023年中考数学压轴题训练——三角形
试卷更新日期:2023-05-14 类型:三轮冲刺
一、真题
-
1. 在△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.
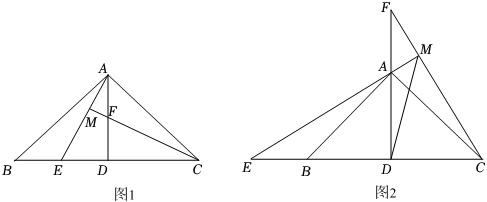 (1)、如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.
(1)、如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 , 位置关系是;(2)、如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.①(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
②连接DM,求∠EMD的度数;
③若DM=6 , ED=12,求EM的长.
2. 已知 ,点A,B分别在射线 上运动, .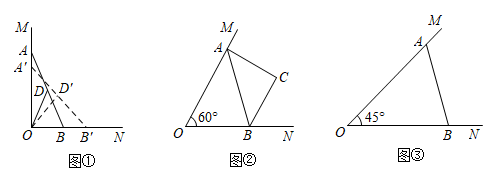 (1)、如图①,若 ,取AB中点D,点A,B运动时,点D也随之运动,点A,B,D的对应点分别为 ,连接 .判断OD与 有什么数量关系?证明你的结论:(2)、如图②,若 ,以AB为斜边在其右侧作等腰直角三角形ABC,求点O与点C的最大距离:(3)、如图③,若 ,当点A,B运动到什么位置时, 的面积最大?请说明理由,并求出 面积的最大值.3. 在△ ABC中,∠BAC=90° ,AB=AC= ,D为 BC的中点,E,F分别为AC, AD 上任意一点,连接EF,将线段EF绕点E顺时针旋转 90°得到线段EG,连接FG, AG.
(1)、如图①,若 ,取AB中点D,点A,B运动时,点D也随之运动,点A,B,D的对应点分别为 ,连接 .判断OD与 有什么数量关系?证明你的结论:(2)、如图②,若 ,以AB为斜边在其右侧作等腰直角三角形ABC,求点O与点C的最大距离:(3)、如图③,若 ,当点A,B运动到什么位置时, 的面积最大?请说明理由,并求出 面积的最大值.3. 在△ ABC中,∠BAC=90° ,AB=AC= ,D为 BC的中点,E,F分别为AC, AD 上任意一点,连接EF,将线段EF绕点E顺时针旋转 90°得到线段EG,连接FG, AG.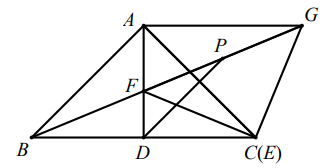
 (1)、如图1,点 E 与点 C 重合,且 GF 的延长线过点 B ,若点 P 为 FG 的中点,连接 PD,求 PD的长;(2)、如图 2,EF 的延长线交 AB 于点M,点N在 AC上, ∠AGN=∠AEG 且GN=MF,求证:AM+AF= AE(3)、如图3,F为线段 AD上一动点,E为 AC的中点,连接BE,H为直线BC上一动点,连接 EH,将△ BEH沿EH翻折至△ABC所在平面内,得到△ B'EH',连接 B'G,直接写出线段 B'G的长度的最小值4.
(1)、如图1,点 E 与点 C 重合,且 GF 的延长线过点 B ,若点 P 为 FG 的中点,连接 PD,求 PD的长;(2)、如图 2,EF 的延长线交 AB 于点M,点N在 AC上, ∠AGN=∠AEG 且GN=MF,求证:AM+AF= AE(3)、如图3,F为线段 AD上一动点,E为 AC的中点,连接BE,H为直线BC上一动点,连接 EH,将△ BEH沿EH翻折至△ABC所在平面内,得到△ B'EH',连接 B'G,直接写出线段 B'G的长度的最小值4. (1)、【问题提出】
(1)、【问题提出】
如图1,是等边的中线,点P在的延长线上,且 , 则的度数为.(2)、【问题探究】
如图2,在中,.过点A作 , 且 , 过点P作直线 , 分别交于点O、E,求四边形的面积.(3)、【问题解决】
如图3,现有一块型板材,为钝角,.工人师傅想用这块板材裁出一个型部件,并要求.工人师傅在这块板材上的作法如下:①以点C为圆心,以长为半径画弧,交于点D,连接;
②作的垂直平分线l,与于点E;
③以点A为圆心,以长为半径画弧,交直线l于点P,连接 , 得.
请问,若按上述作法,裁得的型部件是否符合要求?请证明你的结论.
5. 综合与实践 (1)、知识再现
(1)、知识再现
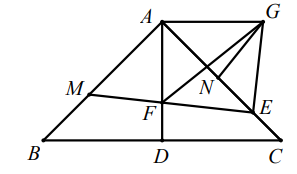
如图 , 中, , 分别以、、为边向外作的正方形的面积为、、 . 当 , 时, .(2)、问题探究如图,中, .
如图 , 分别以、、为边向外作的等腰直角三角形的面积为、、 , 则、、之间的数量关系是 .(3)、如图 , 分别以、、为边向外作的等边三角形的面积为、、 , 试猜想、、之间的数量关系,并说明理由.(4)、实践应用
如图4,将图中的绕点逆时针旋转一定角度至 , 绕点顺时针旋转一定角度至 , 、相交于点 . 求证:;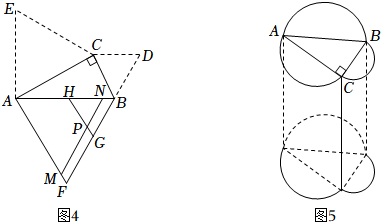 (5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.6. 如图,在△ABC中,∠ABC=30°,AB=AC,点O为BC的中点,点D是线段OC上的动点(点D不与点O,C重合),将△ACD沿AD折叠得到三角形AED,连接BE.
(5)、如图5,分别以图中的边、、为直径向外作半圆,再以所得图形为底面作柱体,、、为直径的半圆柱的体积分别为、、 . 若 , 柱体的高 , 直接写出的值.6. 如图,在△ABC中,∠ABC=30°,AB=AC,点O为BC的中点,点D是线段OC上的动点(点D不与点O,C重合),将△ACD沿AD折叠得到三角形AED,连接BE.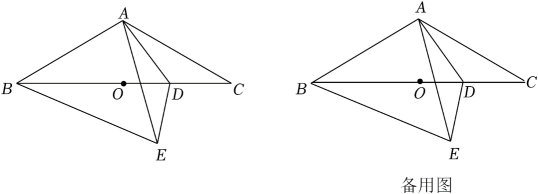 (1)、当时,;(2)、探究与之间的数量关系,并给出证明;(3)、设 , 的面积为x,以AD为边长的正方形的面积为y,求y关于x的函数解析式.
(1)、当时,;(2)、探究与之间的数量关系,并给出证明;(3)、设 , 的面积为x,以AD为边长的正方形的面积为y,求y关于x的函数解析式.二、模拟预测
-
7. 已知 E在△ABC内部(如图①),等边三角形ABC的边长为6,等边三角形BDE的边长为4,连结AE和DC
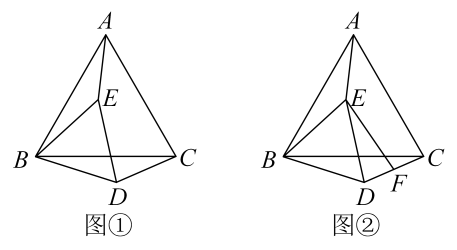 (1)、求证AE=DC;(2)、当AE⊥BD时,求CD的长;(3)、将△BDE绕点B旋转一周,F为DC的中点(如图②),求旋转过程中EF的取值范围.8. 综合与实践
(1)、求证AE=DC;(2)、当AE⊥BD时,求CD的长;(3)、将△BDE绕点B旋转一周,F为DC的中点(如图②),求旋转过程中EF的取值范围.8. 综合与实践小明遇到这样一个问题,如图1,中, , , 点D为的中点,求的取值范围.
小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长到E,使 , 连接 , 构造 , 经过推理和计算使问题得到解决
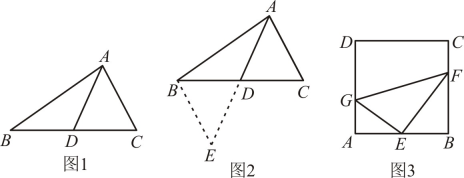
请回答:
(1)、小明证明用到的判定定理是:____;(填入你选择的选项字母)A、 B、 C、 D、(2)、的取值范围是.(3)、小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.
参考小明思考问题的方法,解决问题:
如图3,在正方形中,E为边的中点,G、F分别为 , 边上的点,若 , , , 求的长.9. 综合与探究问题提出:某兴趣小组在综合与实践活动中提出这样一个问题:在等腰直角三角板中, , D为的中点,用两根小木棒构建角,将顶点放置于点D上,得到 , 将绕点D旋转,射线 , 分别与边交于E,F两点,如图1所示.
 (1)、操作发现:如图2,当E,F分别是的中点时,试猜想线段与的数量关系是;(2)、类比探究:如图3,当E,F不是的中点,但满足时,求证;(3)、拓展应用:如图4,将两根小木棒构建的角,放置于边长为4的正方形纸板上,顶点和正方形对角线的中点O重合,射线分别与交于E,F两点,且满足 , 请求出四边形的面积.10. 在中, , , D是射线上一动点,连接 , 以为边作 , 在右侧,与过点A且垂直于的直线交于点E,连接 .
(1)、操作发现:如图2,当E,F分别是的中点时,试猜想线段与的数量关系是;(2)、类比探究:如图3,当E,F不是的中点,但满足时,求证;(3)、拓展应用:如图4,将两根小木棒构建的角,放置于边长为4的正方形纸板上,顶点和正方形对角线的中点O重合,射线分别与交于E,F两点,且满足 , 请求出四边形的面积.10. 在中, , , D是射线上一动点,连接 , 以为边作 , 在右侧,与过点A且垂直于的直线交于点E,连接 .
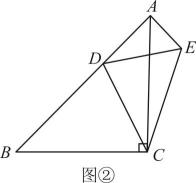
 (1)、当都在的左侧时,如图①,线段之间的数量关系是;(2)、当在的两侧时,如图②,线段之间有怎样的数量关系?写出你的猜想,并给予证明;(3)、当都在AC的右侧时,如图③,线段之间有怎样的数量关系?直接写出你的猜想,不必证明.11. 综合运用.(1)、如图(),已知:在中, , , 直线经过点 , , , 垂足分别为点 , . 证明: .
(1)、当都在的左侧时,如图①,线段之间的数量关系是;(2)、当在的两侧时,如图②,线段之间有怎样的数量关系?写出你的猜想,并给予证明;(3)、当都在AC的右侧时,如图③,线段之间有怎样的数量关系?直接写出你的猜想,不必证明.11. 综合运用.(1)、如图(),已知:在中, , , 直线经过点 , , , 垂足分别为点 , . 证明: . (2)、如图(),将()中的条件改为:在中, , , , 三点都在直线上,并且有 , 其中为任意锐角或钝角.请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
(2)、如图(),将()中的条件改为:在中, , , , 三点都在直线上,并且有 , 其中为任意锐角或钝角.请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由. (3)、拓展与应用:如图(), , 是 , , 三点所在直线上的两动点( , , 三点互不重合),点为平分线上的一点,且和均为等边三角形,连接 , , 若 , 试判断的形状并说明理由.
(3)、拓展与应用:如图(), , 是 , , 三点所在直线上的两动点( , , 三点互不重合),点为平分线上的一点,且和均为等边三角形,连接 , , 若 , 试判断的形状并说明理由.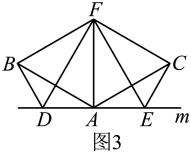 12. 如图1,在中, , , 点为的中点,过点作射线交于点 , 点为射线上一动点,过点作于点 , 点为边上一点,连结 , 且满足 , 设 , .
12. 如图1,在中, , , 点为的中点,过点作射线交于点 , 点为射线上一动点,过点作于点 , 点为边上一点,连结 , 且满足 , 设 , . (1)、求线段的长;(2)、求关于的函数表达式;(3)、如图2,连结.
(1)、求线段的长;(2)、求关于的函数表达式;(3)、如图2,连结.①当为等腰三角形时,求的值.
②以点为旋转中心,将线段按顺时针方向旋转得线段 , 当点落在边上时,求的值.
13. 如图,在中, , , , 动点P从点A出发,沿AB以每秒3个单位长度的速度向终点B匀速运动.同时,动点Q从点A出发,沿AC以每秒4个单位长度的速度向终点C匀速运动,连接PQ,将绕点P顺时针旋转90°得到 , 设点P的运动时间为t秒. (1)、用含t的代数式表示线段的长度为 .(2)、当点N落在直线BC上时,求t的值.(3)、连接QN,线段QN的中点记为点E,连接PE,当线段PE与的某条边的长度相等时,求t的值.(4)、当与重叠部分为四边形时,是否存在一点O,使点O到这个四边形的各个顶点的距离都等于?若存在,直接写出t的值,若不存在,说明理由.14. 在中, , , 是的角平分线,于点 .
(1)、用含t的代数式表示线段的长度为 .(2)、当点N落在直线BC上时,求t的值.(3)、连接QN,线段QN的中点记为点E,连接PE,当线段PE与的某条边的长度相等时,求t的值.(4)、当与重叠部分为四边形时,是否存在一点O,使点O到这个四边形的各个顶点的距离都等于?若存在,直接写出t的值,若不存在,说明理由.14. 在中, , , 是的角平分线,于点 . (1)、如图1,连接 , 求证:是等边三角形;(2)、点是线段上的一点(不与点 , 重合),以为一边,在的下方作 , 交延长线于点 . 请你在图2中画出完整图形,并直接写出 , 与之间的数量关系;(3)、如图3,点是线段上的一点,以为一边,在的下方作 , 交延长线于点 . 试探究 , 与数量之间的关系,并说明理由.15. 翻开数学发展史,我们就知道数学不仅是抽象、严谨的,还有另外一面,人类从结绳计数开始就在进行着数学实验,并且通过实验不断发展数学,可见,数学实验不仅是数学家研究数学的方式,也是学生学习数学的一种重要方式,在某次数学社团活动中,几位同学利用三角板进行了如下的实数学验,请大家在这一数学实验的基础上思考并回答相关问题:几位同学把两块完全相同的等腰直角三角板按图1方式摆放,已知 , , , , , 线段在直线上,点F在线段上,点A与点D重合.
(1)、如图1,连接 , 求证:是等边三角形;(2)、点是线段上的一点(不与点 , 重合),以为一边,在的下方作 , 交延长线于点 . 请你在图2中画出完整图形,并直接写出 , 与之间的数量关系;(3)、如图3,点是线段上的一点,以为一边,在的下方作 , 交延长线于点 . 试探究 , 与数量之间的关系,并说明理由.15. 翻开数学发展史,我们就知道数学不仅是抽象、严谨的,还有另外一面,人类从结绳计数开始就在进行着数学实验,并且通过实验不断发展数学,可见,数学实验不仅是数学家研究数学的方式,也是学生学习数学的一种重要方式,在某次数学社团活动中,几位同学利用三角板进行了如下的实数学验,请大家在这一数学实验的基础上思考并回答相关问题:几位同学把两块完全相同的等腰直角三角板按图1方式摆放,已知 , , , , , 线段在直线上,点F在线段上,点A与点D重合. (1)、 , ;(2)、将三角板的直角顶点F沿方向滑动,同时顶点D沿方向在射线上滑动,如图2.
(1)、 , ;(2)、将三角板的直角顶点F沿方向滑动,同时顶点D沿方向在射线上滑动,如图2.①当点F恰好是线段中点时,求的度数;
②当点F从初始位置滑动到点A处时,请直接写出点E所经过的路径长;
(3)、在(2)的条件下,过点D,F分别作 , 的垂线,两条垂线相交于点P,连接 , 线段的长度是否为定值?如果是,请求出结果;如果不是,请说明理由.16. 已知在等腰直角三角形中, , , . (1)、如图1,请直接写出点C的坐标 , 若点C在反比例函数上,则;(2)、如图2,若将延x轴向右平移得到 , 平移距离为m,当 , 都在反比例函数上时,求 , m;(3)、如图3,在(2)的条件下,在y轴上是否存在点P,使得的面积是面积的一半.若存在,请求出点P;若不存在,请说明理由.
(1)、如图1,请直接写出点C的坐标 , 若点C在反比例函数上,则;(2)、如图2,若将延x轴向右平移得到 , 平移距离为m,当 , 都在反比例函数上时,求 , m;(3)、如图3,在(2)的条件下,在y轴上是否存在点P,使得的面积是面积的一半.若存在,请求出点P;若不存在,请说明理由.