2023年浙教版数学八年级下学期期末复习——难点专练
试卷更新日期:2023-05-14 类型:复习试卷
一、单选题
-
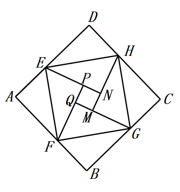
1. 如图,正方形ABCD由8个全等的直角三角形和小正方形PQMN组成,记正方形ABCD、正方形EFGH、正方形PQMN的面积为x 、y、z.若EF的长为 ,则 x+y+z=( )
 A、12 B、18 C、 D、2. 如图,矩形ABCD和矩形CEFG,AB=1,BC=CG=2,CE=4,点P在边GF上,点Q在边CE上,且PF=CQ,连结AC和PQ,N,M分别是AC,PQ的中点,则MN的长为( )
A、12 B、18 C、 D、2. 如图,矩形ABCD和矩形CEFG,AB=1,BC=CG=2,CE=4,点P在边GF上,点Q在边CE上,且PF=CQ,连结AC和PQ,N,M分别是AC,PQ的中点,则MN的长为( )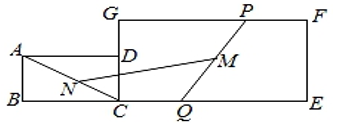 A、3 B、6 C、 D、3. 设m是整数,关于x的方程mx2-(m-1)x+1=0有有理根,则方程的根为( )。A、 B、x=-1 C、 D、有无数个根4. 如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )
A、3 B、6 C、 D、3. 设m是整数,关于x的方程mx2-(m-1)x+1=0有有理根,则方程的根为( )。A、 B、x=-1 C、 D、有无数个根4. 如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )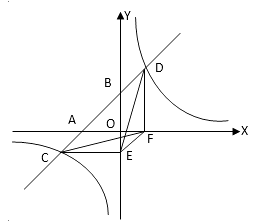 A、2 B、3 C、4 D、55. 设a、b是整数,方程x2+ax+b=0的一根是 ,则 的值为( )
A、2 B、3 C、4 D、55. 设a、b是整数,方程x2+ax+b=0的一根是 ,则 的值为( )
A、2 B、0 C、-2 D、-1二、填空题
-
6. 如图,P为Rt△ABC内一点,其中∠BAC=90°,并且PA=3,PB=7,PC=9,则BC的最大值为.
 7. 如图所示,已知矩形 中, , 现将边 绕它的一个端点旋转,当另一端点恰好落在边 所在直线的点E处时,线段 的长度为
7. 如图所示,已知矩形 中, , 现将边 绕它的一个端点旋转,当另一端点恰好落在边 所在直线的点E处时,线段 的长度为 8. 如图,▱ABCD中,AC,BD交于O,AE平分∠BAD,EC=CD=1,∠ECD=2∠CDA.下列结论:①AC平分∠EAD;②OE= AD;③BD= ;④S▱ABCD= .正确的有个.
8. 如图,▱ABCD中,AC,BD交于O,AE平分∠BAD,EC=CD=1,∠ECD=2∠CDA.下列结论:①AC平分∠EAD;②OE= AD;③BD= ;④S▱ABCD= .正确的有个. 9. 如图,点 是边长为 的菱形 对角线 上的一个动点,点 分别是 边上的中点,则 的最小值是.
9. 如图,点 是边长为 的菱形 对角线 上的一个动点,点 分别是 边上的中点,则 的最小值是. 10. 如图把边长为3的正方形AOBC放置于直角坐标系中,顶点O 在坐标原点处,点A,B分别在y轴,x轴的正半轴上,点D是OB的中点,AD⊥DE,DE与正方形外角平分线BE交于点E,若 轴上存在点P使得四边形CPDE为平行四边形,则点P的坐标为.
10. 如图把边长为3的正方形AOBC放置于直角坐标系中,顶点O 在坐标原点处,点A,B分别在y轴,x轴的正半轴上,点D是OB的中点,AD⊥DE,DE与正方形外角平分线BE交于点E,若 轴上存在点P使得四边形CPDE为平行四边形,则点P的坐标为.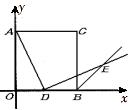 11. 由四个正方形相框拼成的照片墙如图所示,已知正方形 ,正方形 ,正方形 的.面积分别为4平方分米,4平方分米, 平方分米,则正方形 的面积为平方分米.
11. 由四个正方形相框拼成的照片墙如图所示,已知正方形 ,正方形 ,正方形 的.面积分别为4平方分米,4平方分米, 平方分米,则正方形 的面积为平方分米.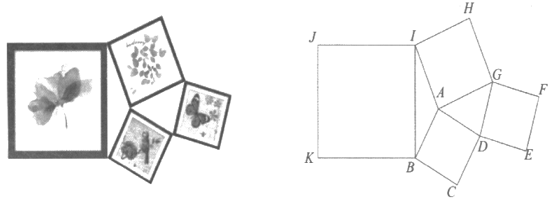 12. 如图,在矩形 中, ,将 沿射线 平移得到 ,连接 ,则 的最小值是.
12. 如图,在矩形 中, ,将 沿射线 平移得到 ,连接 ,则 的最小值是. 13. 如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是.
13. 如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是.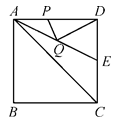 14. 如图,点O是▱ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=
14. 如图,点O是▱ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF= AB;G,H分别是BC边上的点,且GH=
AB;G,H分别是BC边上的点,且GH=  BC,若S1 , S2分别表示△EOF和△GOH的面积,则S1与S2之间的数量关系是 .
BC,若S1 , S2分别表示△EOF和△GOH的面积,则S1与S2之间的数量关系是 .  15. 若a≠b,且 则 的值为16. 若方程 的根也是方程 的根,则 .17. 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点
15. 若a≠b,且 则 的值为16. 若方程 的根也是方程 的根,则 .17. 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF. (1)、四边形ABEF是;(选填矩形、菱形、正方形、无法确定)(直接填写结果)(2)、AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 , ∠ABC=°.(直接填写结果)18. 定义:几个全等的正多边形依次有一边重合,排成一圈,中间可以围成一个正多边形,我们称作正多边形的环状连接。
(1)、四边形ABEF是;(选填矩形、菱形、正方形、无法确定)(直接填写结果)(2)、AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 , ∠ABC=°.(直接填写结果)18. 定义:几个全等的正多边形依次有一边重合,排成一圈,中间可以围成一个正多边形,我们称作正多边形的环状连接。如图,我们可以看作正六边形的环状连接,中间围成一个边长相等的正六边形;
若正八边形作环状连接,中间可以围的正多边形的边数为;
若边长为1的正n边形作环状连接,中间围成的是等边三角形,则这个环状连接的外轮廓长为。
 19. 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB= S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为.
19. 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB= S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为. 20. 如图,一次函数y=-2x+b与反比例函数y= (x>0)的图象交于A,B两点,连结OA,过B作BD⊥x轴于点D,交OA于点C,若CD:CB=1:8,则b=.
20. 如图,一次函数y=-2x+b与反比例函数y= (x>0)的图象交于A,B两点,连结OA,过B作BD⊥x轴于点D,交OA于点C,若CD:CB=1:8,则b=. 21. 已知(x﹣2016)2+(x﹣2018)2=80,则(x﹣2017)2= .22. 若实数x,y,m满足等式 ,则m+4的算术平方根为 .23. 如图,在边长为1的菱形 ABCD中,∠ABC=120°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠ACE=120°.连接AE,再以AE为边作第三个菱形AEGH,使 ∠AEG=120°,…,按此规律所作的第n个菱形的边长是 .
21. 已知(x﹣2016)2+(x﹣2018)2=80,则(x﹣2017)2= .22. 若实数x,y,m满足等式 ,则m+4的算术平方根为 .23. 如图,在边长为1的菱形 ABCD中,∠ABC=120°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠ACE=120°.连接AE,再以AE为边作第三个菱形AEGH,使 ∠AEG=120°,…,按此规律所作的第n个菱形的边长是 .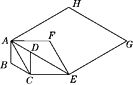 24. 一次棋赛,有n个女选手和9n个男选手,每位参赛者与其 个选手各对局一次,计分方式为:胜者的2分,负者得0分,平局各自得1分。比赛结束后统计发现所有参赛男选手的分数和是所有女选手的分数和的4倍,则n的所有可能值是.
24. 一次棋赛,有n个女选手和9n个男选手,每位参赛者与其 个选手各对局一次,计分方式为:胜者的2分,负者得0分,平局各自得1分。比赛结束后统计发现所有参赛男选手的分数和是所有女选手的分数和的4倍,则n的所有可能值是.
25. 如图,点 为直线 上的两点,过 两点分别作y轴的平行线交双曲线 ( )于 两点. 若 ,则 的值为.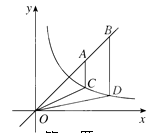 26. 如图,一次函数y=﹣x+b与反比例函数y= (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
26. 如图,一次函数y=﹣x+b与反比例函数y= (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.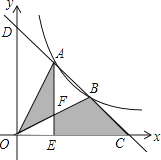 (1)、b=(用含m的代数式表示);(2)、若S△OAF+S四边形EFBC=4,则m的值是 .
(1)、b=(用含m的代数式表示);(2)、若S△OAF+S四边形EFBC=4,则m的值是 .三、解答题
-
27. 在平行四边形ABCD中,∠BAD=α,DE平分∠ADC,交对角线AC于点G,交射线AB于点E,将线段EB绕点E顺时针旋转 α得线段EP.
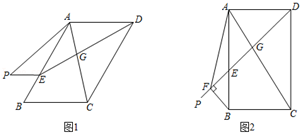 (1)、如图1,当α=120°时,连接AP,请写出线段AP和线段AC的数量关系,并说明理由;(2)、如图2,当α=90°时,过点B作BF⊥EP于点F,连接AF,请写出线段AF,AB,AD之间的数量关系,并说明理由;(3)、当α=120°时,连接AP,若BE AB,直接写出△APE与△CDG面积的比值.28. 如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE.
(1)、如图1,当α=120°时,连接AP,请写出线段AP和线段AC的数量关系,并说明理由;(2)、如图2,当α=90°时,过点B作BF⊥EP于点F,连接AF,请写出线段AF,AB,AD之间的数量关系,并说明理由;(3)、当α=120°时,连接AP,若BE AB,直接写出△APE与△CDG面积的比值.28. 如图,AC平分∠BAD,∠DCA=∠CAD,在CD的延长线上截取DE=DA,连接AE. (1)、求证:AB∥CD;(2)、若AE=5,AC=12,求线段CE的长;(3)、在(2)的条件下,若线段CE上有一点P,使△DPA的面积是△ACD面积的六分之一,求PC长.
(1)、求证:AB∥CD;(2)、若AE=5,AC=12,求线段CE的长;(3)、在(2)的条件下,若线段CE上有一点P,使△DPA的面积是△ACD面积的六分之一,求PC长.