2023年浙教版数学八年级下学期期末复习——反比例函数难点专练
试卷更新日期:2023-05-14 类型:复习试卷
一、单选题
-
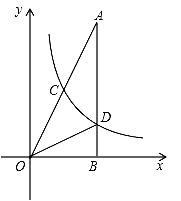
1. 如图,一次函数与反比例函数的图象相交于、两点,与轴,轴分别相交于、两点,连接、 . 过点作轴于点 , 交于点 . 设点的横坐标为 . 若 , 则的值为( )
 A、1 B、 C、2 D、42. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( )
A、1 B、 C、2 D、42. 如图,菱形的四个顶点均在坐标轴上,对角线交于原点O,交于点G,反比例函数的图象经过线段的中点E,若 , 则的长为( ) A、 B、 C、 D、3. 如图,直线AC与反比例函数y=(x>0)的图象交于A,C两点(点A在点C的左边),与x轴交于点B,以点A为顶点向下作矩形ADMN,其对角线相交于点O,且AD平分∠OAB,AC=CB,连结CD,若△ACD的面积为6,则k的值为( )
A、 B、 C、 D、3. 如图,直线AC与反比例函数y=(x>0)的图象交于A,C两点(点A在点C的左边),与x轴交于点B,以点A为顶点向下作矩形ADMN,其对角线相交于点O,且AD平分∠OAB,AC=CB,连结CD,若△ACD的面积为6,则k的值为( ) A、8 B、10 C、12 D、164. 两个反比例函数和在第一象限内的图象如图所示,点在的图象上,轴于点 , 交的图象于点 , 轴于点 , 交的图象于点 , 轴于点 , 当点在图象上运动时,以下结论:①与始终平行;②与始终相等;③四边形的面积不会发生变化;④的面积等于四边形的面积.其中一定正确的是( )
A、8 B、10 C、12 D、164. 两个反比例函数和在第一象限内的图象如图所示,点在的图象上,轴于点 , 交的图象于点 , 轴于点 , 交的图象于点 , 轴于点 , 当点在图象上运动时,以下结论:①与始终平行;②与始终相等;③四边形的面积不会发生变化;④的面积等于四边形的面积.其中一定正确的是( )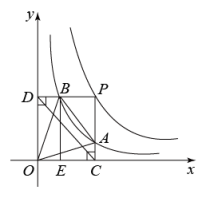 A、①②③ B、①②④ C、①③④ D、②③④5. 如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y= (k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是( )
A、①②③ B、①②④ C、①③④ D、②③④5. 如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y= (k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是( )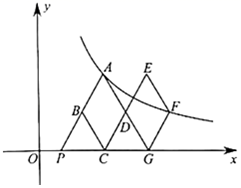 A、3 B、3 C、6 D、66. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )
A、3 B、3 C、6 D、66. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )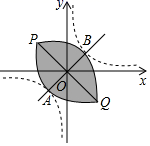 A、 B、 C、2 D、47. 如图,在直角坐标系中,直线 的图象上有8个点,从左往右依次记为 , ,…, (横坐标依次增加2个单位),要使这些点平均分布在函数 的图象两侧,每侧4个点,则 可以取到的整数值有( )
A、 B、 C、2 D、47. 如图,在直角坐标系中,直线 的图象上有8个点,从左往右依次记为 , ,…, (横坐标依次增加2个单位),要使这些点平均分布在函数 的图象两侧,每侧4个点,则 可以取到的整数值有( ) A、7个 B、8个 C、9个 D、10个8. 如图所示,已知 为反比例函数 图象上的两点,动点 在 轴正半轴上运动,当 的值最大时,连结 , 的面积是 ( )
A、7个 B、8个 C、9个 D、10个8. 如图所示,已知 为反比例函数 图象上的两点,动点 在 轴正半轴上运动,当 的值最大时,连结 , 的面积是 ( ) A、 B、1 C、 D、9. 如图,反比例函数y= (k>0)的图象经过矩形0ABC对角线的交点D,分别交AB、BC于点E、F。若四边形OEBF的面积为6,则k的值为( )
A、 B、1 C、 D、9. 如图,反比例函数y= (k>0)的图象经过矩形0ABC对角线的交点D,分别交AB、BC于点E、F。若四边形OEBF的面积为6,则k的值为( )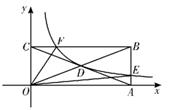 A、1 B、2 C、3 D、410. 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数 在第一象限的图象经过点B , 若 ,则 的值为( ).
A、1 B、2 C、3 D、410. 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数 在第一象限的图象经过点B , 若 ,则 的值为( ). A、6 B、3 C、 D、11. 在平面直角坐标系中,反比例函数 的图象上有三点 ,若 且 ,则B的取值范围为( )A、 B、 C、 D、12. 直线 与双曲线 交于A,B两点,若A,B两点的坐标分别为 , ,则 的值为( ).A、-4 B、0 C、4 D、813. 如图,点A,B在反比例函数y= (x<0)的图象上,连结OA,AB,以OA,AB为边作□OABC,若点C恰好落在反比例函数y= (x>0)的图象上,此时□OABC的面积是( )
A、6 B、3 C、 D、11. 在平面直角坐标系中,反比例函数 的图象上有三点 ,若 且 ,则B的取值范围为( )A、 B、 C、 D、12. 直线 与双曲线 交于A,B两点,若A,B两点的坐标分别为 , ,则 的值为( ).A、-4 B、0 C、4 D、813. 如图,点A,B在反比例函数y= (x<0)的图象上,连结OA,AB,以OA,AB为边作□OABC,若点C恰好落在反比例函数y= (x>0)的图象上,此时□OABC的面积是( )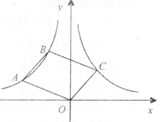 A、3 B、 C、 D、614. 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=的图象上,OA=1,OC=6,则正方形ADEF的面积为( )
A、3 B、 C、 D、614. 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=的图象上,OA=1,OC=6,则正方形ADEF的面积为( ) A、2 B、4 C、6 D、1215. 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, . ∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )
A、2 B、4 C、6 D、1215. 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, . ∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )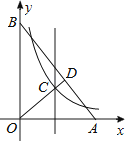 A、2 B、3 C、5 D、716. 将一次函数y=x图象向下平移b个单位,与双曲线y=交于点A,与x轴交于点B,则OA2-OB2=( )A、-2 B、2 C、- D、17. 如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是.若反比例函数的图象经过点B,则此反比例函数表达式为( )
A、2 B、3 C、5 D、716. 将一次函数y=x图象向下平移b个单位,与双曲线y=交于点A,与x轴交于点B,则OA2-OB2=( )A、-2 B、2 C、- D、17. 如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是.若反比例函数的图象经过点B,则此反比例函数表达式为( ) A、 B、 C、 D、18. 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y= 的图象上.那么k的值是( )
A、 B、 C、 D、18. 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y= 的图象上.那么k的值是( ) A、3 B、6 C、12 D、
A、3 B、6 C、12 D、二、填空题
-
19. 在平面直角坐标系xOy中,双曲线y1= (x>0)经过平行四边形ABCD的对称中心Q,双曲线y2= (x>0,0<k<4)经过平行四边形ABCD的顶点B,C,且A(3,0),D(0,4),则k=.
 20. 如图,在平面直角坐标系 中,点 坐标为 ,以 为对角线作正方形 ,若顶点 在反比例函数 的图象上, 的值是.
20. 如图,在平面直角坐标系 中,点 坐标为 ,以 为对角线作正方形 ,若顶点 在反比例函数 的图象上, 的值是. 21. 如图,12个边长为1的正方形摆放在平面直角坐标系中,过点A(-1,0)的直线AB将这12个正方形面积相等的两部分,且直线与反比例函数y= (k<0)的图象交于点C , 与y轴交于点B , 若△AOB与△BOC的面积之比为1:3,则k的值为 .
21. 如图,12个边长为1的正方形摆放在平面直角坐标系中,过点A(-1,0)的直线AB将这12个正方形面积相等的两部分,且直线与反比例函数y= (k<0)的图象交于点C , 与y轴交于点B , 若△AOB与△BOC的面积之比为1:3,则k的值为 . 22. 如图,四边形OACB是平行四边形,OB在x轴上,反比例函数(k>0)在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,△AOF的面积为6,则 k的值为.
22. 如图,四边形OACB是平行四边形,OB在x轴上,反比例函数(k>0)在第一象限内的图象经过点A,与BC交于点F.若点F为BC的中点,△AOF的面积为6,则 k的值为.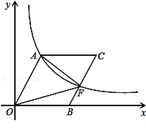 23. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 .
23. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分∠OAE,反比例函数y= (k>0,x>0)的图象经过AE上的两点A,F,且AF=EF,△ABE的面积为18,则k的值为 .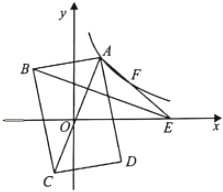
三、解答题
-
24. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长米,另一边长加长米,可得与之间的函数关系式某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数 , 现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整:
 (1)、类比反比例函数可知,函数的自变量的取值范围是 , 这个函数值的取值范围是 .(2)、“数学兴趣小组”进一步思考函数的图象和性质,请根据函数的图象,画出函数的图象;(3)、结合函数的图象解答下列问题:
(1)、类比反比例函数可知,函数的自变量的取值范围是 , 这个函数值的取值范围是 .(2)、“数学兴趣小组”进一步思考函数的图象和性质,请根据函数的图象,画出函数的图象;(3)、结合函数的图象解答下列问题:①求出方程的根;
②如果方程有2个实数根,请直接写出的取值范围.
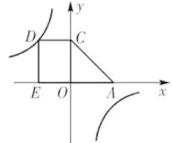
25. 如图,在矩形中, , , 点是边的中点,反比例函数的图象经过点 , 交于点 . (1)、求的值及直线的解析式;(2)、在轴上找一点 , 使的周长最小,求此时点的坐标;(3)、在(2)的条件下,求的面积.26. 如图,点、分别在反比例函数和的图象上,线段与轴相交于点 .
(1)、求的值及直线的解析式;(2)、在轴上找一点 , 使的周长最小,求此时点的坐标;(3)、在(2)的条件下,求的面积.26. 如图,点、分别在反比例函数和的图象上,线段与轴相交于点 .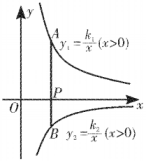
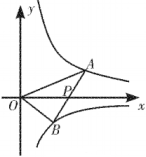
图① 图②
(1)、如图①,若轴,且 , . 求、的值;(2)、如图②,若点是线段的中点,且的面积为2.求的值.27. 如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(1,6),B(6,1)两点.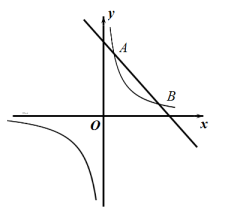 (1)、求一次函数y1的表达式与反比例函数y2的表达式;(2)、当y1>y2时,直接写出自变量x的取值范围为;(3)、在平面内存在点P,使得点A、点B关于点P成中心对称的点恰好落在坐标轴上,请直接写出点P的坐标为.28. 某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变实验发现,当每次漂洗用水量v(升)一定时,衣服中残留的洗衣粉量y(克)与漂洗次数x(次)满足y=(k为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.(1)、求k的值.(2)、如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?(3)、现将20升水等分成x次(x>1)漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?29. 如图,在平面直角坐标系中,四边形为正方形,已知点、 , 点、在第二象限内.
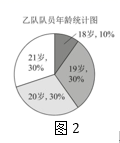
(1)、求一次函数y1的表达式与反比例函数y2的表达式;(2)、当y1>y2时,直接写出自变量x的取值范围为;(3)、在平面内存在点P,使得点A、点B关于点P成中心对称的点恰好落在坐标轴上,请直接写出点P的坐标为.28. 某小组进行漂洗实验,每次漂洗的衣服量和添加洗衣粉量固定不变实验发现,当每次漂洗用水量v(升)一定时,衣服中残留的洗衣粉量y(克)与漂洗次数x(次)满足y=(k为常数),已知当使用5升水,漂洗1次后,衣服中残留洗衣粉2克.(1)、求k的值.(2)、如果每次用水5升,要求漂洗后残留的洗衣粉量小于0.8克,求至少漂洗多少次?(3)、现将20升水等分成x次(x>1)漂洗,要使残留的洗衣粉量降到0.5克,求每次漂洗用水多少升?29. 如图,在平面直角坐标系中,四边形为正方形,已知点、 , 点、在第二象限内.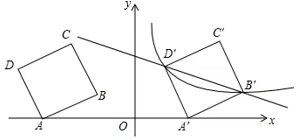 (1)、点的坐标;(2)、将正方形以每秒2个单位的速度沿轴向右平移秒,若存在某一时刻 , 使在第一象限内点、两点的对应点、正好落在某反比例函数的图象上,请求出此时的值以及这个反比例函数的解析式;(3)、在(2)的情况下,问是否存在轴上的点和反比例函数图象上的点 , 使得以、、、四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点的坐标;若不存在,请说明理由.30. 甲、乙两支运动队各有10名队员,他们的年龄分布情况分别如图、表所示:
(1)、点的坐标;(2)、将正方形以每秒2个单位的速度沿轴向右平移秒,若存在某一时刻 , 使在第一象限内点、两点的对应点、正好落在某反比例函数的图象上,请求出此时的值以及这个反比例函数的解析式;(3)、在(2)的情况下,问是否存在轴上的点和反比例函数图象上的点 , 使得以、、、四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点的坐标;若不存在,请说明理由.30. 甲、乙两支运动队各有10名队员,他们的年龄分布情况分别如图、表所示: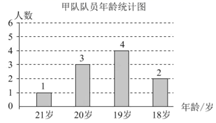
甲、乙两队队员年龄统计表
平均数(近似值)
众数
中位数
甲队
a
①
②
乙队
20
③
b
解决下列问题:
(1)、求甲队队员的平均年龄a的值.(结果取整数)(2)、补全统计表中的①②③三处.(3)、阅读理解-----扇形图中求中位数的方法.[阅读与思考]
小明同学在求乙队队员年龄的中位数b时,是这样思考的:因为中位数是将一组数据按大小排序后,排在中间位置的一个数或中间两个数的平均数,那就需要先找到数据按大小排序后,大致排在50%附近的数,再根据中位数的概念进行细化求解.
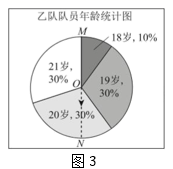
图2这个扇形图中的数据18~21是按大小顺序旋转排列的,我们就可以像图3所示的这样,先找到最大数据“21”与最小数据“18”的分界半径OM,为找到排在50%附近的数,再作出直径MN,那么射线ON指向的数据就是中位数.
王老师的评价:小明的这个方法是从中位数的概念出发,充分利用了扇形图的特性形象直观地解决问题.
[理解与应用]
请你利用小明的方法直接写出统计表中b的值.