2022-2023学年人教版八年级数学下期末复习数据的分析

试卷更新日期：2023-05-13 类型：复习试卷

进入出卷网下载

一、单选题

1. 某女子排球队6名场上队员身高（单位： $cm$ ）是：170，174，178，180，180，184，现用身高为 $178 cm$ 的队员替换下场上身高为 $174 cm$ 的队员，与换人前相比，场上队员的身高（）.

A、平均数变大，中位数不变 B、平均数变大，中位数变大 C、平均数变小，中位数不变 D、平均数变小，中位数变大

查看试题解析
2. 某射击小组有20人，教练根据他们某次射击的数据绘制成如图所示的统计图，则这组数据的众数和中位数分别是（）

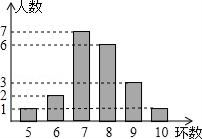A、7，7 B、8，7.5 C、7，7.5 D、8，6.5

查看试题解析
3. 有甲、乙两种糖果，原价分别为每千克a元和b元。根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果。现在糖果价格有了调整：甲种糖果单价下降15%、乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则 $\frac{x}{y}$ 等于（）

A、 $\frac{3 a}{4 b}$ B、 $\frac{4 a}{3 b}$ C、 $\frac{3 b}{4 a}$ D、 $\frac{4 b}{3 a}$

查看试题解析
4. 有甲、乙两个箱子，其中甲箱内有98颗球，分别标记号码1～98，且号码为不重复的整数，乙箱内没有球．已知小育从甲箱内拿出49颗球放入乙箱后，乙箱内球的号码的中位数为40．若此时甲箱内有a颗球的号码小于40，有b颗球的号码大于40，则关于a、b之值，下列何者正确？（　　）

A、a=16 B、a=24 C、b=24 D、b=34

查看试题解析
5.
甲、乙、丙三名射击运动员在某场测试中各射击20次，3人的测试成绩如下表，则甲、乙、丙3名运动员测试成绩最稳定的是（）

A、甲 B、乙 C、丙 D、3人成绩稳定情况相同

查看试题解析
6. 学校食堂午餐有10元，12元、15元三种价格的盒饭供选择，若经过统计发现10元、12元、15元的盒饭卖出数量恰好分别占50%，30%、20%，则卖出盒饭价格的中位数是（）

A、10元 B、11元 C、12元 D、无法确定

查看试题解析
7. 10名同学分成甲、乙两队进行篮球比赛，他们的身高（单位：cm）如下表所示：

队员1
队员2
队员3
队员4
队员5
甲队
177
176
175
172
175
乙队
170
175
173
174
183
设两队队员身高的平均数依次为 $\bar{x}$ _甲， $\bar{x}$ _乙，身高的方差依次为S²_甲， S²_乙，则下列关系中正确的是（　　）

A、 $\bar{x}$ _甲= $\bar{x}$ _乙， S²_甲＞S²_乙 B、 $\bar{x}$ _甲＜ $\bar{x}$ _乙， S²_甲＜S²_乙 C、 $\bar{x}$ _甲＞ $\bar{x}$ _乙， S²_甲＞S²_乙 D、 $\bar{x}$ _甲= $\bar{x}$ _乙， S²_甲＜S²_乙

查看试题解析
8. 某同学统计了4月份某天全国8个城市的空气质量指数，并绘制了折线统计图（如图），则这8个城市的空气质量指数的中位数是（）

A、57 B、40 C、73 D、65

查看试题解析
9. 某服装店店主统计一段时间内某品牌男衬衫39号，40号，41号，43号的销售情况如下表所示．

男衬衫号码

39号

40号

41号

42号

43号

销售数量/件

3

12

21

9

5

他决定进货时，增加41号衬衫的进货数量，影响该店主决策的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
10. 一组数据3、5、8、3、4的众数与中位数分别是（　　）

A、3，8 B、3，3 C、3，4 D、4，3

查看试题解析

二、填空题

11. 某市号召居民节约用水，为了解居民用水情况，随机抽查了20户家庭某月的用水量，结果如下表：

户数

8

6

6

用水量（吨）

4

6

7

则这20户家庭的该月平均用水量为吨.

查看试题解析
12. 若一组数据x₁＋1，x₂＋1，…，x_n＋1的平均数为10，方差为1，则另一组数据3x₁＋2，3x₂＋2，…，3x_n＋2的方差是．

查看试题解析

13. 下表是甲、乙两名同学近五次数学测试（满分均为100分）的成绩统计表：

同学	第一次	第二次	第三次	第四次	第五次
甲	90	88	92	94	91
乙	90	91	93	94	92

根据上表数据，成绩较好且比较稳定的同学是．

查看试题解析

14. 如果一组数据：5，x，9，4的平均数为6，那么x的值是

查看试题解析
15. 已知一组数据23，25，20，15，x，15，若它们的中位数是21，那么它们的平均数为。

查看试题解析

三、解答题

16. 某校在招聘数学教师时以考评成绩确定人选.甲、乙两位高校毕业生的各项考评成绩如下.如果按笔试成绩占30%、模拟上课占60%、答辩占10%来计算各人的考评成绩，那么谁将优先录取？

考评项目	成绩/分
考评项目	甲	乙
理论知识（笔试）	88	95
模拟上课	95	90
答辩	88	90

查看试题解析

17. 受疫情影响，某地无法按原计划正常开学，在延迟开学期间该地区组织了在线教学活动.开学后，某校针对各班在线教学的个性化落实情况，通过初评决定从甲、乙两个班中推荐一个作为在线教学先进班级，下表是这两个班的五项指标（10分制）的考评得分表（单位：分）：

班级	课程设置	课程质量	在线答疑	作业情况	学生满意度
甲班	10	10	6	10	7
乙班	10	8	8	9	8

如果学校把“课程设置”、“课程质量”、“在线答疑”、“作业情况”、“学生满意度”这五项指标得分按照2：2：3：1：2的比例确定最终成绩，则应推荐哪个班为在线教学先进班级？

查看试题解析

18.
为迎接中国共产党建党90周年，某校举办“红歌伴我成长”歌咏比赛活动，参赛同学的成绩分别绘制成频数分布表和频数分布直方图（均不完整）如下：
分数段
频数
频率
80≤x＜85
9
0.15
85≤x＜90
m
0.45
90≤x＜95
■
■
95≤x＜100
6
n
（1）求m，n的值分别是多少；
（2）请在图中补全频数分布直方图；
（3）比赛成绩的中位数落在哪个分数段？

查看试题解析
19. 在校园诗歌朗诵比赛中，采用10位评委现场打分，每位选手的最后得分为去掉一个最低分，去掉一个最高分后的平均分，已知10位评委给某位选手的打分分别是：9.0 9.4 9.3 9.8 9.5 9.1 9.6 9.4 9.7 9.6
求这位选手的最后得分．

查看试题解析
20. 在某中学举行的演讲比赛中，八年级5名参赛选手的成绩如下表所示
选手
1号
2号
3号
4号
5号
得分
92
95
91
89
88
（1）计算出这5名选手的平均成绩；
（2）计算出这5名选手成绩的方差．

查看试题解析
21.
某单位欲从内部公开选拔一名管理人员，对甲、乙、丙三名候选人进行了笔试面试两项测试，三人的测试成绩如下表所示：
测试项目
测试成绩/分
甲
乙
丙
笔试
75
80
90
面试
93
70
68
根据录用程序，组织400名职工对三人利用投票推荐的方式进行民主评议，三人得票率（没有弃权票，每位职工只能推荐1人）如图，每得一票记作1分．
（1）请算出三人的民主评议得分；
（2）根据实际需要，单位将笔试、面试、民主评议三项测试得分按5：3：2的比例确定个人成绩（精确到0.1分），那么谁将被录用？

查看试题解析

22. 为庆祝中国共产党建党100周年，某校举行了“红色华诞，党旗飘扬”党史知识竞赛.为了解竞赛成绩，抽样调查了七，八年级部分学生的分数，过程如下：

（ 1 ）收集数据从该校七.八年级学生中各随机抽取20名学生的分数，其中八年级的分数如下：

81 83 84 85 86 87 87 88 89 90

92 92 93 95 95 95 99 99 100 100

（ 2 ）整理、描述数据按如下分段整理描述样本数据：

分数 $x$

人数

年级

$80 \leq x < 85$

$85 \leq x < 90$

$90 \leq x < 95$

$95 \leq x \leq 100$

七年级

八年级

$a$

（ 3 ）分析数据两组样本数据的平均数、中位数、众数、方差如下表所示：

年级	平均数	中位数	众数	方差
七年级	91	89	97	40.9
八年级	91	$b$	$c$	33.2

根据以上提供的信息，解答下列问题：

①填空： $a =$ ， $b =$ ， $c =$ ；

②样本数据中，七年级甲同学和八年级乙同学的分数都为90分，同学的分数在本年级抽取的分数中从高到低排序更靠前（填“甲”或“乙”）：

③从样本数据分析来看，分数较整齐的是年级（填“七”或“八”）；

④如果七年级共有400人参赛，则该年级约有人的分数不低于95分.

查看试题解析

四、综合题

23. 某零件加工厂为了检查

A

，

B

两个车间所生产同一产品的合格情况，在两个车间内随机抽取了10个样品进行检测，操作流程如下：

$①$ 收集数据 $($ 单位： $m m)$ ：

A车间：178，185，176，177，189，179，181，173，183，189.

B车间：185，175，178，180178，185，179，184，178，188 .

$②$ 整理数据：

车间范围	$170.5 ～ 175.5$	$175.5 ～ 180.5$	$180.5 ～ 185.5$	$185.5 ～ 190.5$
$A$ 车间	1	4	3	2
$B$ 车间	1	$a$	$b$	1

$③$ 分析数据：

车间数据	平均数	众数	中位数	方差
$A$ 车间	181	189	180	26.6
$B$ 车间	181	178	179.5	15.8

$④$ 应用数据 $($ 测量结果 $175.5 m m ～ 185.5 m m$ 范围内的产品为合格 $)$ ：

(1)、求出

a =

，

b =

；

(2)、估计

A

车间生产的1000个该款新产品中合格产品有多少个？

(3)、结合上述数据信息，请判断哪个车间生产的新产品更好，并说明理由.

查看试题解析

	队员1	队员2	队员3	队员4	队员5
甲队	177	176	175	172	175
乙队	170	175	173	174	183

男衬衫号码	39号	40号	41号	42号	43号
销售数量/件	3	12	21	9	5

分数段	频数	频率
80≤x＜85	9	0.15
85≤x＜90	m	0.45
90≤x＜95	■	■
95≤x＜100	6	n

测试项目	测试成绩/分
测试项目	甲	乙	丙
笔试	75	80	90
面试	93	70	68

户数	8	6	6
用水量（吨）	4	6	7

选手	1号	2号	3号	4号	5号
得分	92	95	91	89	88

2022-2023学年人教版八年级数学下期末复习 数据的分析

一、单选题

二、填空题

三、解答题

四、综合题

2022-2023学年人教版八年级数学下期末复习数据的分析