人教版2022-2023学年度第二学期八年级数学 体质健康测试中的数据分析 期末复习
试卷更新日期：2023-05-13 类型：复习试卷
一、单选题
-
1. 据统计，无为市某月4日~10日的最高气温如下发所示，则下列说法错误的是（ ）
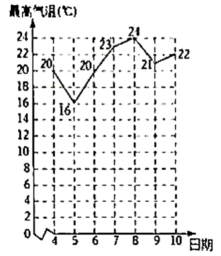A、平均数是20 B、众数是20 C、5日~8日最高气温呈上升趋势 D、中位数是212. 颠球是练习足球球感最基本的招式之一某校足球队10名球员在一次训练中的颠球测试成绩（以“次”为单位计）为：52，50，46，54，50，56，47，52，53，50．则以下数据中计算错误的是（ ）A、平均数为51 B、方差为8.4 C、中位数为53 D、众数为503. 某校“啦啦操”兴趣小组共有50名学生，她们的年龄分布如下表：年龄/岁
12
13
14
15
人数
5
23
■
■
由于表格污损，14岁、15岁人数看不清，则下列关于年龄的统计量可以确定的是（ ）．
A、平均数、众数 B、众数、中位数 C、平均数、中位数 D、中位数、方差4. 太原某中学李老师在期中考试数学成绩登分过程中，出现了一处不符合题意，把数学最高成绩写得更高了．则计算结果一定不受影响的是（ ）A、中位数 B、方差 C、平均数 D、众数5. 一组数据：的平均数为 ， 众数为 ， 中位数为 ， 则以下判断正确的是（ ）A、一定出现在中 B、一定出现在中 C、一定出现在中 D、 ， ， 都不会出现在中6. 甲、乙、丙三名射击运动员在集训期间的测试成绩如下表所以，若需要在其中遴选一名成绩优异并稳定的运动员参加比赛，比较适合的运动员是（ ）成绩/（环）
测试一
测试二
测试三
测试四
平均数
方差
甲
9.2
8.8
9.4
8.6
9.0
0.1
乙
8.8
8.6
8.7
9.1
8.8
0.035
丙
8.8
8.9
9.1
9.3
9.0
0.035
A、甲 B、乙 C、丙 D、无法确定7. 第24届冬季奥林匹克运动会于2022年2月4日在北京隆重开幕，某社区举办了奥林匹克知识竞赛活动，此次竞赛共有10题，七名参赛者在此次竞赛活动中答对的题数分别为7、10、9、9、10、8、10．关于这组数据，下列结论中正确的是（ ）A、方差是7 B、众数是9 C、平均数是8.5 D、中位数是98. 已知数据1，2，3，3，4，5，则下列关于这组数据的说法错误的是（ ）A、众数是3 B、平均数是3 C、方差是2 D、中位数是39. 甲、乙两名学生在参加今年体育考试前各做了5次立定跳远测试，两人的平均成绩相同，其中甲所测得成绩的中位数是2.30m、方差是0.005，乙所测得成绩的中位数是2.35m、方差是0.016，那么成绩较为稳定的同学是（ ）A、乙同学 B、甲、乙两人一样 C、甲同学 D、无法确定10. 为了解新冠肺炎疫情防控期间，学生居家进行“线上学习”情况，某班进行了某学科单元基础知识“线上测试”，其中抽查的名学生的成绩如图所示，对于这名学生的测试成绩，下列说法正确的有（ ）
①中位数是分；②众数是分；③平均数是分；④方差是
A、 B、 C、 D、二、填空题
-
11. 北京冬奥会金牌榜前十位的金牌数分别为16，12，9，8，8，8，7，7，6，5．这组数据的平均数、众数和中位数中，最大的是 ．12. 随着北京冬奥会的成功举办，越来越多的人喜欢上冰雪运动．为了解当地一家滑雪场的经营情况，小聪对该滑雪场自2022年1月31日至2月13日共两周的日接待游客数（单位：千人）进行了统计，并绘制成下面的统计图．
根据统计图提供的信息，有下列三个结论：
①按日接待游客数从高到低排名，2月6日在这14天中排名第4；
②记第一周，第二周日接待游客数的方差分别为s12 ， s22 ， 则s12＞s22；
③这14天日接待游客数的众数和中位数都是2.0千人．
其中所有正确结论的序号是 ．
13. 寒假期间，滑雪冬令营的同学们都参加了“单板滑雪”这个项目的40次的训练测试，每次测试成绩分别为5分，4分，3分，2分，1分五档，甲、乙两位同学在这个项目的测试成绩统计结果如图所示：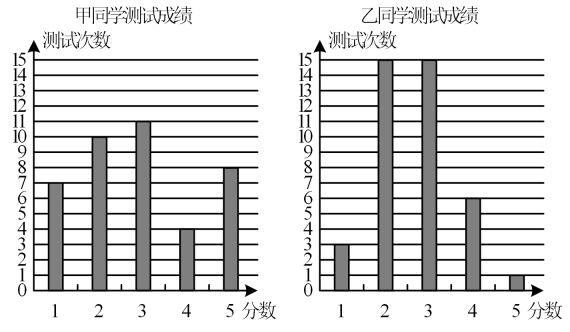
结合图中数据，请你从平均数、众数、中位数、方差中选择一方面评论一下两位同学的滑雪成绩 ．
14. 学校举行演讲比赛，共有15名同学进入决赛，比赛将评出金奖1名，银奖3名，铜奖4名．某参赛选手知道自己的分数后，要判断自己能否获奖，他应当关注的有关 成绩的统计量是 （填“平均数”、“中位数”或“众数”）．15. 某校举行“汉字听写选拔赛”，七、八年级各有位同学组队参加比赛．赛后统计成绩发现两队成绩的平均分都是分，且七年级队成绩的方差是 ， 八年级队成绩的方差是 ， 由此推断：七、八年级两队中成绩较为稳定的是队．三、解答题
-
16. 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示．
成绩/m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
分别计算这些运动员成绩的平均数、中位数、众数（结果保留小数点后两位）．
17. 某社区为了增强居民节约用水的意识，随机调查了部分家庭一年的月均用水量（单位：t）．根据调查结果，绘制出如下的统计图①和图②．
请根据相关信息，解答下列问题：
（Ⅰ）本次接受调查的家庭个数为 ，图①中m的值为 ；
（Ⅱ）求统计的这组月均用水量数据的平均数、众数和中位数．
18. 为了解某学校九年级学生每周平均课外阅读时间的情况，随机抽查了该学校九年级部分同学，对其每周平均课外阅读时间进行统计，绘制了如下的统计图①和图②.请根据相关信息，解答下列问题：
（Ⅰ）该校抽查九年级学生的人数为 ， 图①中的m值为 ；
（Ⅱ）求统计的这组数据的众数、中位数和平均数.
（Ⅲ）根据统计的样本数据，估计该校九年级400名学生中，每周平均课外阅读时间大于的学生人数.
四、综合题
-
19. 某中学280名学生参加植树节活动，要求每人植3至6棵，活动结束后随机抽查了若干名学生每人的植树量，并分为四种类型，A：3棵；B：4棵；C：5棵；D： 6棵，将各类的人数绘制成扇形图(如图1)和条形图(如图2) ．
回答下列问题：
(1)、这次调查一共抽查了 ▲ 名学生的植树量；请将条形图补充完整；(2)、被调查学生每人植树量的众数是棵，中位数是棵；(3)、求被调查学生每人植树量的平均数，并估计这280名学生共植树多少棵？20. 我校举行“文学经典我来诵”为主题的红色经典朗诵比赛，七，八年根据初赛成绩，各选出5个班级组成七年级代表队和八年级代表队参加学校决赛，两个队各选出的5个班级的决赛成绩如图所示.平均数（分）
中位数（分）
众数（分）
七年级队
____
85
____
八年级队
85
____
100
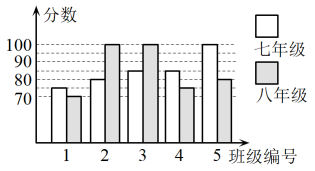(1)、根据图示填写表；(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？(3)、计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定.21. 疫情防控已成为常态化，为了解学生对疫情防控措施的知晓情况，某校对八（1）班和八（2）班开展了“疫情防控知识”问卷测试，并对八（1）班和八（2）班随机各抽取了5位同学的成绩进行比较，如下表：八（1）班
100
90
100
70
80
八（2）班
90
95
90
85
100
(1)、计算两个班级样本中的五位同学的平均成绩、众数、中位数；(2)、分析样本数据，哪个班级成绩稍好，请说明理由.22. 八年级两个班各选派10名学生参加“垃圾分类知识竞赛，各参赛选手的成绩如下：八(I)班：88，91，92，93，93，93，94，98，98，100；
八(2)班：89，93，93，93，95，96，96，98，98，99．
通过整理，得到数据分析表如下
班级
最高分
平均分
中位数
众数
方差
八(1)班
100
94
93
b
c
八(2)班
99
95
a
93
8.4
(1)、求表中a，b，c的值：(2)、依据数据分析表，有同学认为最高分在(1)班，(1)班的成绩比(2)班好，但也有同学认为(2)班的成绩更好，请你写出两条支持八(2)班成绩更好的理由．23. 本学期开学初，学校体育组对九年级某班50名学生进行了跳绳项目的测试，根据测试成绩制作了下面两个统计图.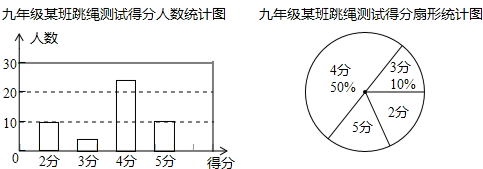
根据统计图解答下列问题：
(1)、本次测试的学生中，得4分的学生有多少人(2)、本次测试的平均分是多少分中位数是多少众数是多少(3)、通过一段时间的训练，体育组对该班学生的跳绳项目进行第二次测试，测得成绩的最低分为3分，且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中得4分、5分的学生各有多少人