人教版2022-2023学年度第二学期八年级数学 数据的波动程度 期末复习

试卷更新日期：2023-05-13 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 已知一组数据的方差为S2＝15［(x1－10)2＋(x2－10)2＋…＋(x5－10)2］，则（ ）
    A、这组数据有10个 B、这组数据的平均数是5 C、方差是一个非负数 D、每个数据加3，方差的值增加3

    查看试题解析

  • 2. 对于一组数据-1，-1，4，2，下列结论不正确的是（ ）
    A、平均数是1 B、方差是3.5 C、中位数是0.5 D、众数是-1

    查看试题解析

  • 3. 对甲、乙两同学100米短跑进行5次测试，他们的成绩通过计算得x¯甲=x¯乙 ， S甲2=0.25 ， S乙2=0.016 ， 下列说法正确的是（ ）
    A、甲、乙两人的短跑成绩一样稳定 B、乙比甲的短跑成绩稳定 C、甲比乙的短跑成绩稳定 D、无法确定谁的短跑成绩更稳定

    查看试题解析

  • 4. 在方差的计算公式S2=110[(x1−20)2+(x2−20)2+...+(x10−20)2]中，数字10和20表示的意义分别是（  ）
    A、数据得个数和平均数 B、数据的方差和平均数 C、数个数和方差 D、以上都不对

    查看试题解析

  • 5. 有甲、乙两组数据，如下表所示：

    甲

    11

    12

    13

    14

    15

    乙

    12

    12

    13

    14

    14

    两组数据的方差分别是s甲2、s乙2 ， 则s甲2与s乙2的大小关系为（  ）

    A、s甲2<s乙2 B、s甲2>s乙2 C、s甲2≤s乙2 D、s甲2≥s乙2

    查看试题解析

  • 6. 若x1 ， x2 ， x3 ， ⋯，xn的平均数为8，方差为2，则关于x1＋2，x2＋2，x3＋2，……，xn＋2，下列结论正确的是（  ）
    A、平均数为8，方差为2 B、平均数为8，方差为4 C、平均数为10，方差为2 D、平均数为10，方差为4

    查看试题解析

  • 7. 为了从四名同学中选出一人参加计算机编程比赛，对他们进行了多次测试，并对每个人的测试成绩的平均数及方差进行了统计（如下表），则应选的同学是（  ）

    学生

    学生一

    学生二

    学生三

    学生四

    平均数

    95

    96

    96

    95

    方差

    5

    5

    4.8

    4.8

    A、学生一 B、学生二 C、学生三 D、学生四

    查看试题解析

  • 8. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩平均数均为9环，方差分别为：s甲2=0.56 ， s乙2=0.48 ， s丙2=0.58 ， s丁2=0.52 ， 则成绩最稳定的是（ ）．
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 9. 甲、乙、丙、丁四人进行射击测试，四人10次射击成绩的平均数都是8.8环，方差分别为s甲2=0.65 ， s乙2=0.54 ， s丙2=0.48 ， s丁2=0.42 ， 则四人中成绩最稳定的是（ ）
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 10. 为备战2024年巴黎奥运会，甲、乙两名运动员训练测验，两名运动员的平均分相同，且s甲 2=0.02 ， s乙 2=0.002 ， 则成绩较稳定的是（ ）
    A、乙运动员 B、甲运动员 C、两运动员一样稳定 D、无法确定

    查看试题解析

二、填空题

  • 11.  小明用S2=110[(x1−2)2+(x2−2)2+…+(x10−2)2]计算一组数据的方差，那么x1+x2+x3+…+x10=  .

    查看试题解析

  • 12. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数x¯(单位：千克)及方差s2 ， 如表所示.今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是.(填“甲”或“乙”或“丙”或“丁”)


    甲

    乙

    丙

    丁

    x¯

    24

    24

    23

    20

    S2

    2.1

    1.9

    2

    1.9

    查看试题解析

  • 13. 已知数据x1 ， x2 ，…，xn的平均数是2，方差是3，则一组新数据2x1+4，2x2+4，…，2xn+4的平均数是 ， 方差是.

    查看试题解析

  • 14. 某少年军校准备从甲、乙、丙三位同学中选拔一个参加全市射击比赛.他们在选拔比赛中，射靶十次的平均环数是x甲¯=x乙¯=8.3 ， x丙¯=8；方差分别是，s2甲=1.5 ， s2乙=2.8 ， s2丙=1.5 ， 那么根据以上提供的信息，你认为应该被推荐参加全市射击比赛的同学是.

    查看试题解析

  • 15. 某校要从甲、乙两名同学中选取一名成绩稳定的同学去参加数学竞赛，已知五次模拟测试中统计所得的信息为x¯甲＝115，S甲2＝12，x¯乙＝115，S乙2＝36，则应选择参加竞赛．

    查看试题解析

三、解答题

  • 16. 如图，是甲、乙两名射击运动员一次训练中10次射击环数折线统计图，请判断甲、乙两名射击运动员中谁的成绩的方差小，并计算其方差.

    查看试题解析

  • 17. 某学校为选拔数学能力突出的学生参加中学生数学竞赛，组织了多次测试，其中甲乙两位同学成绩较为优秀，他们在六次赛前测试中的成绩（单位：分）如下表所示．

    甲

    80

    75

    90

    64

    88

    95

    乙

    84

    80

    88

    76

    79

    85

    如果根据这六次成绩选拔其中一人参加比赛，你认为哪一位比较合适？为什么？

    查看试题解析

  • 18. 甲、乙两名射击运动员各进行10次射击，甲的成绩是7，7，8，9，8，9，10，9，9，9．乙的成绩如图所示（单位：环）

     

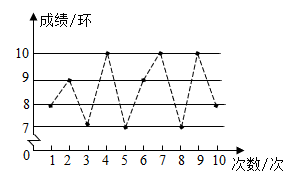    (1)、分别计算甲、乙两人射击成绩的平均数；
    (2)、若要选拔一人参加比赛，应派哪一位？请说明理由．

    查看试题解析

四、综合题

  • 19. 某校对甲，乙两人的射击成绩进行了测试，测试成绩如表：             
       

     第一次 

         		 

     第二次 

         		 

     第三次 

         		 

     第四次 

         		 

     第五次 

     
     

     甲命中环数 

         		 

     7 

         		 

     8 

         		 

     8 

         		 

     8 

         		 

     9 

     
     

     乙命中环数 

         		 

     10 

         		 

     6 

         		 

     10 

         		 

     6 

         		 

     8 

     
    (1)、分别求出甲，乙两人射击成绩的平均数和方差； 
    (2)、现要从甲，乙两人中选拔一人参加比赛，你认为挑选哪一位较合适，请说明理由. 

    查看试题解析

  • 20. 我校举行“文学经典我来诵”为主题的红色经典朗诵比赛，七，八年根据初赛成绩，各选出5个班级组成七年级代表队和八年级代表队参加学校决赛，两个队各选出的5个班级的决赛成绩如图所示.

     

    平均数（分）

    中位数（分）

    众数（分）

    七年级队

    ____

    85

    ____

    八年级队

    85

    ____

    100

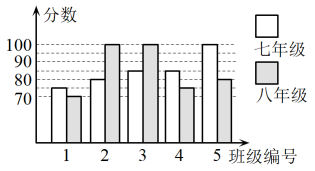    (1)、根据图示填写表；
    (2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？
    (3)、计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定.

    查看试题解析

  • 21. 某校组织八，九年级各500名学生举行“学习二十大，筑梦向未来”知识竞赛，现分别在八，九年级中各随机抽取10名学生的竞赛成绩（单位：分）进行统计、整理如下：

    【收集数据】

    八年级：74，76，79，81，84，86，87，90，90，93.

    九年级：76，81，81，82，82，82，84，85，90，92.

    【整理数据】

    年级

    70≤x<80

    80≤x<90

    90≤x<100

    八年级

    3

    4

    3

    九年级

    1

    a

    2

    【分析数据】

    年级

    平均数

    中位数

    众数

    方差

    八年级

    b

    85

    90

    36.4

    九年级

    83.5

    c

    82

    19.25

    【应用数据】

    (1)、根据以上信息，可以求出：a= ， b= ， c=；
    (2)、在计算这两组数据的方差时用的公式是s2=(x1−x¯)2+(x2−x¯)2+⋅⋅⋅+(xn−x¯)2n ， 其中在计算八年级这组数据的方差时，公式中的n=；
    (3)、根据以上数据，你认为在此次竞赛中哪个年级的成绩更好？请说明理由（写出一条理由即可）.

    查看试题解析

  • 22. 某实验中学八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛，其预赛成绩如图所示：

    (1)、根据上图填写下表：


    平均数

    众数

    中位数

    方差

    甲班

    8.5

    8.5

    0.7

    乙班

    8.5

    8

    1.6

    (2)、请你分别从平均数、众数、中位数和方差四个方面评价甲、乙两班的预赛成绩，并说明你的理由；
    (3)、乙班小明说：“我的成绩是中等水平”，你知道他是几号选手？

    查看试题解析

  • 23. 某学校组织七、八年级全体学生举行了安全知识竞赛活动，为了解竞赛成绩情况，为两个年级各随机抽取10名学生的成绩（满分为100分）进行了分析，并依据分析结果绘制了如下表所示的不完整统计表：

    七年级：90，95，95，80，85，90，80，90，85，100；

    八年级：85，85，95，80，95，90，90，90，100，90．

    年级

    平均数

    中位数

    众数

    方差

    七年级

    89

    m

    90

    39

    八年级

    n

    90

    p

    q

    根据以上信息解答下面问题：

    (1)、填空：m＝　   　 ， p＝ 　   　；
    (2)、求q的值；
    (3)、通过数据分析，你认为哪个年级的成绩比较好？说明理由．

    查看试题解析