人教版2022-2023学年度第二学期八年级数学变量与函数期末复习

试卷更新日期：2023-05-13 类型：复习试卷

进入出卷网下载

一、单选题

1. 在全民健身越野赛中，甲、乙两选手的行程 $y (k m)$ 随时间 $x (h)$ 变化的图像（全程）如图所示.给出下列四种说法：①起跑后 $1 h$ 内，甲在乙的前面；②第 $1 h$ 两人都跑了 $10 k m$ ；③甲比乙先到达终点；④两人都跑了 $20 k m$ .其中正确的是（）

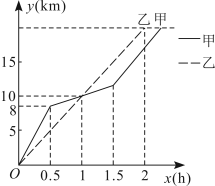A、① B、①② C、①②④ D、②③④

查看试题解析
2. 在函数 $y = \frac{\sqrt{x - 2}}{x}$ 中，自变量x的取值范围是（）

A、 $x \neq 0$ B、 $x > 2$ C、 $x \geq 2$ D、 $x > 0$

查看试题解析
3. 设x、y为实数，且 $y = 2 + \sqrt{3 - x} + \sqrt{x - 3}$ ，则 $| x - y |$ 的值是（）

A、1 B、5 C、2 D、0

查看试题解析
4. 小李与小陆从A地出发，骑自行车沿同一条路行驶到B地，他们离出发地的距离s(单位：km)和行驶时间t(单位：h)之间的函数关系的图象如图所示，根据图中提供的信息，有下列说法：
①他们都行驶了20 km；②小陆全程共用了1.5 h；③小李与小陆相遇后，小李的速度大于小陆的速度；④小李在途中停留了0.5 h. 其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
5. 一本笔记本5元，买x本共付y元，则变量是（）

A、5 B、5和x C、x D、x和y

查看试题解析
6. 如图表示的是嘉淇父母外出散步时，离家的距离与时间的函数关系．（ $a$ 图代表嘉淇的母亲， $b$ 图代表嘉淇的父亲）
①嘉淇的父母出去散步，从家走了20分钟到一个离家900米的报亭；②母亲随即按原来的速度返回；③父亲在报亭看报10分钟；④然后父亲用15分钟返回家．

以上描述，符合函数图象的是（）

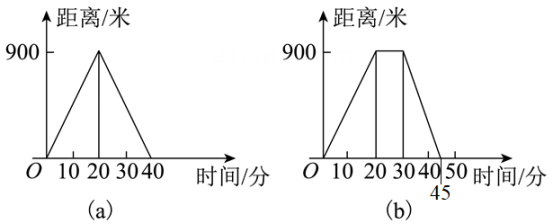A、①③ B、②④ C、①②③ D、①②③④

查看试题解析
7. 弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的质量x（kg）间有下面的关系：
X
0
1
2
3
4
5
Y
10
10.5
11
11.5
12
12.5
下列说法错误的是（）

A、x与y都是变量，且x是自变量； B、所挂物体质量为4kg时，弹簧长度为12cm； C、弹簧不挂重物时的长度为0cm； D、物体质量每增加1kg，弹簧长度y增加0.5cm．

查看试题解析
8. 下列图象中不能表示y是x的函数的是（）．

A、 B、 C、 D、

查看试题解析
9. 下列关系式中y不是x的函数是（）

A、 $y = \pm \sqrt{x} (x > 0)$ B、 $y = - \sqrt{2 x} (x > 0)$ C、 $y = x^{2}$ D、 $y = {(\sqrt{x})}^{2} (x > 0)$

查看试题解析
10. 有一艘货船从甲港沿直线匀速航行到乙海港，航行途中，发现有一包货物落在水中，便掉头寻找，找到货物后，原地进行打捞，打捞起货物后，按原来的速度到达乙港．若水流的速度忽略不记，设货船出发时间为t，货船离乙港的距离为s，则s与t之的函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 函数y＝ $\frac{1}{\sqrt{x - 2}} + \sqrt{4 - x}$ 中自变量的取值范围是.

查看试题解析
12. 如图，△ABC中，AB＝AC，CD⊥AB于D，BD＝1，设BC＝x，AD＝y，当x＞ $\sqrt{2}$ 时，y关于x的函数解析式为．

查看试题解析
13. 已知y﹣1与x成正比例，当x＝2时，y＝9．那么当y＝﹣15时，x的值为．

查看试题解析
14. 函数 $y = {\begin{array}{l} 3 - x (0 \leq x \leq 2) \\ x - 1 (2 \leq x \leq 4) \end{array}$ 的图像如图所示，则这个函数的最小值是．

查看试题解析
15. 某单位组织职工对某地进行绿化，已知绿化面积S（m²）与工作时间t（h）之间的函数关系如图所示，则4小时结束时，绿化面积为m²。

查看试题解析

三、解答题

16. 等腰三角形的周长是16，求出底边长y与一腰长x的函数关系式，并求出自变量x的取值范围？

查看试题解析
17. 小仙骑车从学校回家，中途在十字路口等红灯用了1分钟，然后继续骑车回家．若小仙骑车的速度始终不变，从出发开始计时，小仙离家的距离s（单位：米）与时间t（单位：分钟）的对应关系如图所示，根据图中信息，求小仙骑车的速度及该十字路口与小仙家的距离．

查看试题解析
18. 小强骑自行车去交游，下图表示他离家的距离y（千米）与所用的时间x（小时）之间的函数图象，根据图象所提供的数据，请你写出3个信息.

查看试题解析

四、综合题

19. 如图，正方形ABCD的边长为6cm，P，Q两动点同时从点C出发，点P沿CB→BA以3cm/s的速度向终点A匀速运动，点Q沿CD→DB以2cm/s的速度向点B匀速运动，当点P到达终点A时，点Q同时停止运动．设点P的运动时间为t（s），△CPQ的面积为S（cm²）．

(1)、填空：点P的运动时间为 s；

(2)、求S关于t的函数解析式，并直接写出自变量t的取值范围．

查看试题解析
20. 已知y－4与x成正比例，且当x=－1时， $y = 2$ ．

(1)、求y与x的函数关系式

(2)、当 $y = - 2$ 时，求x的值．

查看试题解析
21. 甲网店对某款水果推出试吃活动：5千克及以内为试吃价：超出5千克的部分恢复原价．邮费都为20元，总价 $y_{甲}$ （单位：元）与购买水果质量 $x$ (单位：千克之间的函数图象如图所示．线下乙店的同款水果售价为每千克8元．

(1)、甲网店该款水果的试吃价为元千克，原价为元 $/$ 千克；

(2)、购买该款水果的质量在什么范围时，在甲店购买比在乙店购买省钱？

(3)、若乙店对该款水果推出降价促销活动，每千克降价 $a$ 元 $(a < 8)$ ，当 $a$ 满足什么条件时，在乙店购买始终比在甲店购买省钱？

查看试题解析
22. 已知一次函数 $y = k x + 4$ 的图象经过点（1，2）．

(1)、求出函数的关系式，并画出其函数图象；

(2)、直接写出该函数图象与x轴的交点坐标，与y轴的交点的交点坐标；

(3)、利用图象说明当x为何范围时，y≥0．

查看试题解析
23. 在平面直角坐标系中，函数 $y = {\begin{array}{l} 2 x + m (x \geq 0) \\ m x - 2 (x < 0) \end{array}$ 的图象记作G（其中m为常数，且m≠0），点M坐标为 $(- 2 ， 1)$ ，点N坐标为（3，1）．

(1)、当图象过点N时，求m的值．

(2)、在（1）的条件下．
①在给定的平面直角坐标系内画出图象G．
②当 $- 2 \leq x \leq 1$ 时，求函数值y的最大值和最小值．

(3)、当图象G与线段MN只有一个交点时，直接写出m的取值范围．

查看试题解析

X	0	1	2	3	4	5
Y	10	10.5	11	11.5	12	12.5

人教版2022-2023学年度第二学期八年级数学 变量与函数 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

人教版2022-2023学年度第二学期八年级数学变量与函数期末复习