人教版2022-2023学年度第二学期八年级数学 平行四边形 期末复习
试卷更新日期：2023-05-13 类型：复习试卷
一、单选题
-
1. 如图，▱的周长是 ， 对角线与交于点 ， ， 是中点，的周长比的周长多 ， 则的长为（ ）
A、5 B、 C、4 D、2. 如图，▱ABCD的对角线AC，BD交于点O，AE平分∠BAD，交BC于点E，且∠ADC＝60°，AB＝BC，连接OE，下列结论：①∠CAD＝30°；②OD＝AB；③S▱ABCD＝AC•CD；④S四边形OECD＝S△AOD ， 其中成立的个数为（ ）
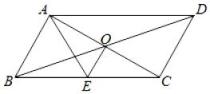A、1个 B、2个 C、3个 D、4个3. 下列条件中，不能判断四边形ABCD是平行四边形的是（ ）A、AB=CD，AD∥BC B、∠A=∠C，∠A+∠B=180° C、AD=BC，AD∥BC D、∠A=∠C，∠B=∠D4. 如图，将平行四边形ABCD沿对角线AC折叠，使点B落在点B'处，若∠1=48°，∠2=32°，则∠B的度数为（ ）
A、124° B、114° C、104° D、56°5. 将6张宽为1的小长方形如图摆放在平行四边形ABCD中，则平行四边形ABCD的周长为（ ）
A、8+4 B、16+4 C、8+8 D、16+86. 如图，四边形的对角线、交于点 ， 下列条件不能判定四边形为平行四边形的是（ ）
A、 ， B、 ， C、 ， D、 ，7. 在四边形ABCD中，AB∥CD且AB=CD，若∠B=56°，则∠C的度数是（ ）A、56° B、65° C、114° D、124°8. 如图 ， 平行四边形中， ， 为锐角.要在对角线上找点N， ， 使四边形为平行四边形，现有图中的甲、乙、丙三种方案，则正确的方案是（ ）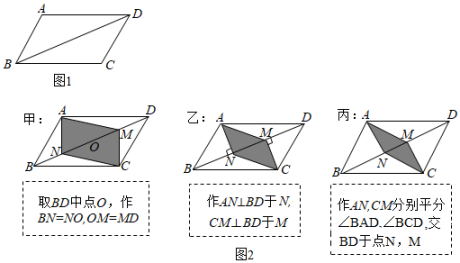
A、只有甲、乙才是 B、只有甲、丙才是 C、只有乙、丙才是 D、甲、乙、丙都是9. 如图，在中， ， 为中线，延长至点E，使 ， 连接 ， F为的中点，连接 ， 若 ， ， 则的长为（ ）
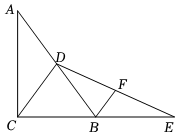A、 B、 C、 D、10. 如图，在 ▱ ABCD中，过对角线BD上任意一点P作EF∥BC，GH∥AB，且AH＝2HD，若△HDP的面积为1，则 ▱ ABCD的面积为（ ）
A、9 B、6 C、12 D、18二、填空题
-
11. 如图，将一副三角板在平行四边形中作如下摆放，设 ， 那么 .
12. 如图所示，已知平行四边形的顶点的坐标为 ， 顶点 ， 分别在轴和直线上，则对角线的最小值是 .
13. 如图，在△ABC中，点D，E分别是AB，AC的中点，连结BE，若AE＝6，DE＝5，∠BEC＝90°，则BE＝.
14. 如图，矩形ABCD中，AB＝2 ，BC＝4，连结对角线AC，E为AC的中点，F为AB边上的动点，连结EF，作点C关于EF的对称点C′，连结C′E，C′F，若△EFC′与△ACF的重叠部分（△EFG）面积等于△ACF的 ，则BF＝.
15. 如图，为了测量池塘边A、B两地之间的距离，在线段AB的同侧取一点C，连结CA并延长至点D，连结CB并延长至点E，使得A、B分别是CD、CE的中点，若DE=18m，则线段AB的长度是m．
三、解答题
-
16. 如图，在ABCD中，AE⊥BC于点E，延长BC至点F，使CF=BE，连接DF，求证：四边形AEFD是矩形．
17. 已知：如图，在ABCD中，E、F为AC上的两点，且AE=CF，连接BE、DF，求证：BE=DF．
18. 已知：如图，点E，F分别为的边BC，AD上的点，且.求证：.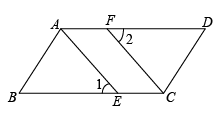
四、综合题
-
19. 如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC于F，交直线MN于E，连接CD、BE．
(1)、求证：CE=AD；(2)、当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由．20. 如图，在平面直角坐标系中，四边形ABCO是平行四边形，O为坐标原点，点A的坐标是（-16，0），线段BC交y轴于点D，点D的坐标是（0，8），线段CD＝6.动点P从点O出发，沿射线OA的方向以每秒2个单位的速度运动，同时动点Q从点D出发，以每秒1个单位的速度向终点B运动，当点Q运动到点B时，点P随之停止运动，运动时间为t秒.
(1)、用t的代数式表示：BQ＝ ， AP＝；(2)、若以A，B，Q，P为顶点的四边形是平行四边形时，求t的值；(3)、当△BQP恰好是等腰三角形时，求t的值.21. 如图，▱ABCD的对角线AC，BD相交于点O，E，F分别是OB，OD的中点，连接AE，AF，CE，CF.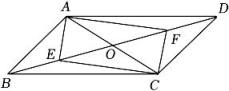
(1)、求证：四边形AECF是平行四边形；(2)、若AB⊥AC，AB＝3，BC＝5.①求AC的长；
②求BD的长.
