人教版2022-2023学年度第二学期八年级数学勾股定理的逆定理期末复习

试卷更新日期：2023-05-13 类型：复习试卷

进入出卷网下载

一、单选题

1. 以下列各组数为边长，能组成直角三角形的是（）

A、1，3，5 B、 $\frac{3}{5}$ ， $\frac{4}{5}$ ， 1 C、 $\sqrt{2}$ ， 2 $\sqrt{2}$ ， 3 D、6，8，9

查看试题解析
2. 已知a、b、c是三角形的三边长，若满足(a-6)²+ $\sqrt{b - 8}$ +|c-10|=0，则这个三角形的形状是（）

A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形

查看试题解析
3. 如图所示的一段楼梯，高BC是3米，斜边AB长是5米，现打算在楼梯上铺地毯，至少需要地毯的长度为（）

A、5米 B、6米 C、7米 D、8米

查看试题解析
4. 如图是一圆柱玻璃杯，从内部测得底面半径为 $6 c m$ ，高为 $16 c m$ ，现有一根长为 $25 c m$ 的吸管任意放入杯中，则吸管露在杯口外的长度最少是（）

A、 $6 c m$ B、 $5 c m$ C、 $9 c m$ D、 $(25 - 2 \sqrt{73}) c m$

查看试题解析
5. 如图，平行四边形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O$ ， $A E ⊥ B C$ ，垂足为 $E$ ， $A B = \sqrt{5}$ ， $A C = 2$ ， $B D = 2 \sqrt{6}$ ，则 $A E$ 的长为（）

A、 $\frac{\sqrt{10}}{3}$ B、 $2 \sqrt{5}$ C、 $\frac{\sqrt{5}}{3}$ D、 $\frac{2 \sqrt{5}}{3}$

查看试题解析
6. △ABC的三条边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是（）

A、b²＝（a+c）（a-c） B、∠A＝∠B+∠C C、∠A：∠B：∠C＝3：4：5 D、a＝6，b＝8，c＝10

查看试题解析
7. 如图，▱ABCD中，对角线AC、BD相交于O，过点O作OE⊥AC交AD于E，若AE＝4，DE＝3，AB＝5，则AC的长为（）

A、 $3 \sqrt{2}$ B、 $4 \sqrt{2}$ C、 $5 \sqrt{2}$ D、 $\frac{5}{2} \sqrt{2}$

查看试题解析
8. 如图，在 $▱ A B C D$ 中， $M$ 是 $B C$ 的中点，且 $A M = 5$ ， $B D = 12$ ， $A D = \frac{26}{3}$ ，则 $▱ A B C D$ 的面积为（）

A、20 B、40 C、62 D、72

查看试题解析
9. 如图，某自动感应门的正上方A处装着一个感应器，离地面的高度AB为2.5米，一名学生站在C处时，感应门自动打开了，此时这名学生离感应门的距离BC为1.2米，头顶离感应器的距离AD为1.5米，则这名学生身高CD为（）米．

A、0.9 B、1.3 C、1.5 D、1.6

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = 4$ ， $B C = 3$ ， $A C = 5$ ，将 $△ A B C$ 折叠，使 $A B$ 边落在 $A C$ 边上，展开后得到折痕 $A D$ ，则 $B D$ 的长度为（）

A、2 B、 $\frac{3}{2}$ C、 $\frac{4}{3}$ D、 $\frac{5}{4}$

查看试题解析

二、填空题

11. 已知等腰 $△ A B C$ 的底边 $B C = 5$ ， D是腰 $A B$ 上一点，且 $C D = 4$ ， $B D = 3$ ，则 $A D$ 的长为.

查看试题解析
12. 如图，网格中的每个小正方形的边长都是1，点A、B、C是小正方形的顶点，则 $∠ A B C$ 的度数为 $°$ .

查看试题解析
13. 如图，在Rt△ABC中，∠ACB=90°，AB=6，分别以AC、BC为一边向外部作正方形，它们的面积分别为S₁、S₂ ，则S₁+S₂的值为

查看试题解析
14. 某工程队负责挖掘一处通山隧道，为了保证山脚A，B两处出口能够直通，工程队在工程图上留下了一些测量数据（此为山体俯视图，图中测量线拐点处均为直角，数据单位：米）．据此可以求得该隧道预计全长米．

查看试题解析
15. 某会展中心在会展期间准备将高5m、长13m、宽2m的楼道铺上地毯，已知地毯每平方米20元，请你帮助计算一下，铺完这个楼道至少需要元．

查看试题解析

三、解答题

16. 岳池中学校园建设中，有一块四边形的空地ABCD．如下图所示，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，AD=4m，BC=12m，CD=13m，若每平方米草皮需要200元，问学校需要投入多少资金买草皮？

查看试题解析
17. 如图，D为 $△ A B C$ 边 $B C$ 上的一点， $A B = 20$ ， $A C = 13$ ， $A D = 12$ ， $D C = 5$ ，求 $B D$ 的长.

查看试题解析
18. 如图，有两只猴子在一棵树CD高6m的点B处，他们都要到A处的池塘去喝水，其中一只猴子沿树爬下去到离树12m处的池塘A处，另一只猴子爬到树顶D后直线越向池塘的A处，如果两只猴子所经过的路程相等，这棵树高有多少米？

查看试题解析

四、综合题

19. 为了把“广安民用运输机场选址岳池普安”宣传到各村，普安镇政府采用了移动宣讲的形式进行宣传动员如图，笔直公路MN的一侧点A处有一村庄，村庄A到公路MN的距离为800米，假使宣讲车P周围1000米以内能听到广播宣传，宣讲车P在公路MN上沿PN方向行驶时：

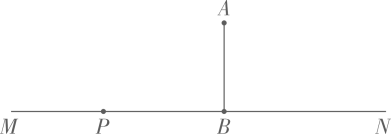(1)、请问村庄能否听到宣传，并说明理由；

(2)、如果能听到，已知宣讲车的速度是每分钟300米，那么村庄总共能听到多长时间的宣传？

查看试题解析
20. 如图，小彭同学每天乘坐地铁上学，他观察发现，地铁D出口和学校O在南北方向的街道的同一边，相距80米，地铁A出口在学校的正东方向60米处，地铁B出口离D出口100米，离A出口 $100 \sqrt{2}$ 米.

(1)、求∠ABD的度数；

(2)、地铁B出口离学校O的距离为米.

查看试题解析
21. 如图，一架梯子AB斜靠在某个过道竖直的左墙上，顶端在点A处，底端在水平地面的点B处．保持梯子底端B的位置不变，将梯子斜靠在竖直的右墙上，此时梯子的顶端在点C处，AO⊥OD，CD⊥OD．测得顶端A距离地面的高度AO为2米，OB为1.5米

(1)、求梯子AB的长；

(2)、若顶端C距离地面的高度CD比AO多0.4米，求OD的长．

查看试题解析
22. 如图，在OABC中，AB=9，AC=12，BC=15．

(1)、求证：△ABC是直角三角形；

(2)、若点P为线段AC上一点，连接BP，且BP=CP，求AP的长。

查看试题解析
23. 观察下列各组勾股数的组成特点，
第1组： $3 = 2 \times 1 + 1$ ， $4 = 2 \times 1 \times (1 + 1)$ ， $5 = 2 \times 1 \times (1 + 1) + 1$ ；

第2组： $5 = 2 \times 2 + 1$ ， $4 = 2 \times 2 \times (2 + 1)$ ， $13 = 2 \times 2 \times (2 + 1) + 1$ ；

第3组： $7 = 2 \times 3 + 1$ ， $24 = 2 \times 3 \times (3 + 1)$ ， $25 = 2 \times 3 \times (3 + 1) + 1$ ；

第4组： $9 = 2 \times 4 + 1$ ， $40 = 2 \times 4 \times (4 + 1)$ ， $41 = 2 \times 4 \times (4 + 1) + 1$ ；

…

第7组：a，b，c．

(1)、写出第7组勾股数a，b，c各是多少．

(2)、写出第n组勾股数，并证明．

查看试题解析

人教版2022-2023学年度第二学期八年级数学 勾股定理的逆定理 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

人教版2022-2023学年度第二学期八年级数学勾股定理的逆定理期末复习