人教版2022-2023学年度第二学期八年级数学 勾股定理 期末复习
试卷更新日期：2023-05-13 类型：复习试卷
一、单选题
-
1. 如图，在△ABC中，∠B=60°，AD⊥BC交BC的延长线于点D，AB=6，BC=2，则AC的长为（ ）
A、2 B、2 C、3 D、2.52. 如图，在△ABC中，∠BAC=90°，∠C=30°，点E是AC的中点，点D在BC上，且CD=AB+BD，若DE=3，则AC的长为（ ）
A、3 B、6 C、6 D、93. 如图，在正方形ABCD中，点E，F在对角线AC上，AC=12．若点E，F是AC的三等分点，点P在正方形ABCD的边上从点A开始按逆时针方向运动一周，直至返回点A，则在此过程中PE+PF的最小值为（ ）
A、4 B、4 C、6 D、64. 如图，矩形ABCD的顶点A，B在数轴上，点A表示-2，AB=2，AD=1．若以点A为圆心，对角线AC的长为半径作弧，交数轴的正半轴于点M，则点M所表示的数为（ ）
A、 B、-1 C、-2 D、-35. 如图， ， 将直角三角形沿着射线方向平移 ， 得三角形已知 ， 则阴影部分的周长为（ ）
A、 B、 C、 D、6. 将6张宽为1的小长方形如图摆放在平行四边形ABCD中，则平行四边形ABCD的周长为（ ）
A、8+4 B、16+4 C、8+8 D、16+87. 如图，四边形ABCD是平行四边形，∠BAC=90°，BD=10，AC=6，则AB的长为（ ）
A、4 B、5 C、6 D、88. 如图，以直角三角形三边长为边作正方形，则字母B所代表的正方形的面积是（ ）
A、12 B、144 C、13 D、1949. 如图，菱形ABCD的顶点A；B分别在y轴正半轴，x轴正半轴上，点C的横坐标为10，点D的纵坐标为8，若直线AC平行x轴，则菱形ABCD的边长值为（ ）
A、9 B、 C、6 D、310. 如图，在中， ， .分别以、为圆心，以大于的长为半径作弧，两弧分别交于、两点，连接直线 ， 分别交、于点、 ， 连接 ， 则的面积为（ ）
A、10 B、12 C、14 D、16二、填空题
-
11. 如图，在△ABC中，点D，E分别是AB，AC的中点，连结BE，若AE＝6，DE＝5，∠BEC＝90°，则BE＝.
12. 如图，在△ABC中，∠ABC=90°，点D是边AC的中点，若BD=5，BC=6，则AB= ．
13. 菱形的边长是5cm，一条对角线的长为6cm，则菱形的面积为cm2 ．14. 如图，四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此进行下去……记正方形ABCD的边长为a1=1，按上述方法所作的正方形的边长依次为a2、a3、a4……、an ， 则an=(用含n的式子表示) ．
15. 如图，矩形ABCD中，AC、BD相交于点O且AC=12，如果∠AOD=60°，则DC=.
三、解答题
-
16. △ABC的三边长分别为5，x-2，x+1，若该三角形是以x+1为斜边的直角三角形，求x的值．17. 岳池中学校园建设中，有一块四边形的空地ABCD．如下图所示，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，AD=4m，BC=12m，CD=13m，若每平方米草皮需要200元，问学校需要投入多少资金买草皮？
18. 如图，D为边上的一点， ， ， ， ， 求的长.
四、综合题
-
19. 如图，▱ABCD的对角线AC，BD相交于点O，E，F分别是OB，OD的中点，连接AE，AF，CE，CF.
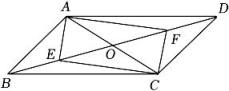(1)、求证：四边形AECF是平行四边形；(2)、若AB⊥AC，AB＝3，BC＝5.①求AC的长；
②求BD的长.
20. 消防车上的云梯示意图如图1所示，云梯最多只能伸长到15米，消防车高3米．如图2，某栋楼发生火灾，在这栋楼的B处有一老人需要救援，救人时消防车上的云梯伸长至最长，此时消防车的位置A与楼房的距离为12米．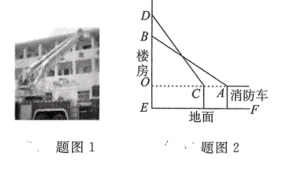
(1)、求B处与地面的距离．(2)、完成B处的救援后，消防员发现在B处的上方3米的D处有一小孩没有及时撤离，为了能成功地救出小孩，则消防车从A处向着火的楼房靠近的距离AC为多少米?21. 如图，在△ABC中，BD平分∠ABC交AC于点D，且BD⊥AC，点F在BC上，点E为AF的中点，连接AF ，BE，ED，DF，BF= DE．
(1)、求证：四边形DEBF是平行四边形．(2)、若AC=DE，BD=6，求AB的长．
