苏科版数学七年级下学期常考题微专练：定义与命题

试卷更新日期：2023-05-13 类型：复习试卷

进入出卷网下载

一、单选题（每空4分，共40分）

1. 下列说法正确的是( )

A、每个定理都有逆定理 B、真命题的逆命题都是真命题 C、每个命题都有逆命题 D、假命题的逆命题都是假命题

查看试题解析
2. 下列命题中，真命题是（）

A、如果a＋b＝0，那么 $| a | = | b |$ B、两个锐角的和是钝角 C、如果一点到线段两端的距离相等，那么这点是这条线段的中点 D、任何数的平方都大于0

查看试题解析
3. 下列命题中，是假命题的是（）

A、等角的余角相等 B、平行于同一条直线的两条直线平行 C、两直线平行，同位角相等 D、若 $a > b$ ，且 $m \neq 0$ ，则 $a m > b m$

查看试题解析
4. 下列命题中，真命题是（）

A、相等的角是对顶角 B、不相交的两条直线是平行线 C、等角的余角相等 D、两条直线被第三条直线所截，同位角相等

查看试题解析
5. 下列命题中的假命题是（）

A、平行于同一条直线的两条直线平行 B、两直线平行，同旁内角互补 C、三角形的一个外角大于任何一个内角 D、直角三角形的两个锐角互余

查看试题解析
6. 下列命题中，属于真命题的是（）

A、如果 $| a | = | b |$ ，那么 $a = b$ B、如果 $a c > b c$ ，那么 $a > b$ C、如果 $a^{2} = b^{2}$ ，那么 $a = b$ D、如果 $a b = 0$ ，那么 $a = 0 或 b = 0$

查看试题解析
7. 下列命题中的真命题是（）

A、相等的角是对顶角 B、内错角相等 C、如果a³＝b³ ，那么a²＝b² D、两个角的两边分别平行，则这两个角相等

查看试题解析
8. 下列四个命题中，是假命题的是（）

A、过直线外一点，有且只有一条直线与已知直线平行 B、两条直线被第三条直线所截，同位角相等 C、三角形任意两边之和大于第三边 D、如果 $a = b$ ， $a = c$ ，那么 $b = c$

查看试题解析
9. 下列命题：①两直线平行，内错角相等；②三角形的外角和是180°；③互为相反数的两个数的和为零； ④若 $n > 1$ ，则 $n^{2} - 1 > 0$ .其中，假命题有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 下列命题与它的逆命题均为真命题的是（）

A、内错角相等 B、对顶角相等 C、如果ab=0，那么a=0 D、互为相反数的两个数和为0

查看试题解析

二、填空题（每空4分，共36分）

11. 命题：“如果a＝b，那么a²＝b²”的逆命题是命题（填“真”或“假”）．

查看试题解析
12. 命题“如果 $x^{2} \geq 1$ ，那么 $x \geq 1$ ”是命题．（选填“真”或“假”）

查看试题解析
13. 命题：“若m=n，则 $m^{2} = n^{2}$ ”的逆命题为.

查看试题解析
14. 命题“正整数是自然数”的逆命题是．

查看试题解析
15. 命题“如果一个三角形的两个角互余，那么这个三角形是直角三角形”的逆命题是：．

查看试题解析
16. 命题“能被5整除的数，它的末位数字是5”的逆命题是.

查看试题解析
17. 命题：“任意两个负数之和是负数”的逆命题是命题.（填“真”或“假”）.

查看试题解析
18. “如果 $a^{2} > b^{2}$ ，那么 $a > b$ ”是假命题，请举出一个反例．在你举出的反例中， $a =$ ， $b =$ ．

查看试题解析

三、解答题（共4题，共44分）

19. 已知：三条不同的直线a、b、c在同一平面内：①a∥b；②a⊥c；③b⊥c； ④a⊥b. 请你用①②③④所给出的其中两个事项作为条件，其中一个事项作为结论(用如果…那么…的形式，写出命题，例如：如果a⊥c、b⊥c、那么a∥b).
⑴写出一个真命题，并证明它的正确性；
⑵写出一个假命题，并举出反例.

查看试题解析
20. 如图，现有以下三个条件：① $A B / / C D ，$ ② $∠ B = ∠ C ，$ ③ $∠ E = ∠ F$ .请你以其中两个作为题设，另一个作为结论构造命题.

(1)、你构造的是哪几个命题？

(2)、你构造的命题是真命题还是假命题？若是真命题，请给予证明；若是假命题，请举出反例（证明其中的一个命题即可）.

查看试题解析
21. 如图，有三个条件：① $∠ 1 = ∠ 2$ ， ② $∠ C = ∠ D$ ， ③ $∠ A = ∠ F$ ，从中任选两个作为已知条件，另一个作为结论，可以组成3个命题，例如：
以③作为结论的命题是：如图，已知 $∠ 1 = ∠ 2$ ， $∠ C = ∠ D$ ，求证： $∠ A = ∠ F$

(1)、请按要求写出命题：
以①作为结论的命题是：；
以②作为结论的命题是：；

(2)、请证明以②作为结论的命题．

查看试题解析
22.

(1)、把下面的证明补充完整：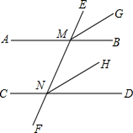

如图，已知直线EF分别交直线AB、CD于点M、N，AB∥CD，MG平分∠EMB，NH平分∠END.求证：MG∥NH

证明：∵AB∥CD（已知）

∴∠EMB＝∠END（    ）

∵MG平分∠EMB，NH平分∠END（已知），

∴∠EMG＝ $\frac{1}{2}$ ∠EMB，∠ENH＝ $\frac{1}{2}$ ∠END（    ），

∴    （等量代换）

∴MG∥NH（    ）.

(2)、你在第（1）小题的证明过程中，应用了哪两个互逆的真命题？请直接写出这一对互逆的真命题.

查看试题解析