浙教版数学八年级下学期期末复习常考题微专练：反比例函数的应用

试卷更新日期：2023-05-13 类型：复习试卷

进入出卷网下载

一、单选题（每题2分，共20分）

1. 某工厂现有原材料100吨，每天平均用去x吨，这批原材料能用y天，则y与x之间的函数表达式为（）

A、 $y = 100 x$ B、 $y = \frac{100}{x}$ C、 $y = \frac{x}{2} + 100$ D、 $y = 100 - x$

查看试题解析
2. 某电子产品的售价为8000元，购买该产品时可分期付款：前期付款3000元，后期每个月分别付相同的数额，则每个月付款额y（元）与付款月数x（x为正整数）之间的函数关系式是（）

A、 $y = \frac{8000}{x} - 3000$ B、 $y = \frac{8000}{x} + 3000$ C、 $y = \frac{3000}{x}$ D、 $y = \frac{5000}{x}$

查看试题解析
3. 如图，某加油站计划在地下修建一个容积为 $2 \times 1 0^{4} m^{3}$ 的圆柱形石油储存室，则储存室的底面积S（单位： $m^{2}$ ）与其深度h（单位：m）的函数图象大致是（）

A、 B、 C、 D、

查看试题解析
4. 要确定方程 $x^{2} + x - 5 = 0$ 的解，只需知道一次函数 $y = x + 1$ 和反比例函数 $y = \frac{k}{x}$ 的图象交点的横坐标．由上面的信息可知， $k$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析
5. 反比例函数 $y = \frac{k}{x}$ 和正比例函数 $y = m x$ 的图象如图所示.由此可以得到方程 $\frac{k}{x} = m x$ 的实数根为（）

A、 $x = 1$ B、 $x = 2$ C、 $x_{1} = 1 ， x_{2} = - 1$ D、 $x_{1} = 1 ， x_{2} = - 2$

查看试题解析
6. 已知一次函数 $y_{1} = x - 1$ 与反比例函数 $y_{2} = \frac{2}{x}$ 的图象交于点 $A (2 ， 1) ， B (- 1 ， - 2)$ ，则 $y_{1} > y_{2}$ 时 $x$ 的取值范围为（）

A、 $x > 2$ B、 $x > 2$ 或 $- 1 < x < 0$ C、 $- 1 < x < 2$ D、 $x > 2$ 或 $x < - 1$

查看试题解析
7. 初三年级甲、乙、丙、丁四个级部举行了知识竞赛，如图，平面直角坐标系中，x轴表示级部参赛人数，y轴表示竞赛成绩的优秀率（该级部优秀人数与该级部参加竞赛人数的比值），其中描述甲、丁两个级部情况的点恰好在同一个反比例函数的图象上，则这四个级部在这次知识竞赛中成绩优秀人数的多少正确的是（）

A、甲 $>$ 乙 $>$ 丙 $>$ 丁 B、丙 $>$ 甲 $=$ 丁 $>$ 乙 C、甲 $=$ 丁 $>$ 乙 $>$ 丙 D、乙 $>$ 甲 $=$ 丁 $>$ 丙

查看试题解析
8. 某个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现．如图所示的是该台灯的电流 $I (A)$ 与电阻 $R (Ω)$ 的关系图象，该图象经过点 $P (880 ， 0.25)$ ．根据图象可知，下列说法正确的是（）

A、当 $I < 0.25$ 时， $R < 880$ B、I与R的函数关系式是 $I = \frac{200}{R} (R > 0)$ C、当 $R > 1000$ 时， $I > 0.22$ D、当 $880 < R < 1000$ 时，I的取值范围是 $0.22 < I < 0.25$

查看试题解析
9. 公元前3世纪，古希腊科学家阿基米德发现了“杠杆原理”：杠杆平衡时，阻力×阻力臂=动力×动力臂，当用撬棍撬动一块石头时，发现阻力和阻力臂分别为 $1200 N$ 和 $0.5 m$ ，关于动力F和动力臂l，下列说法错误的是（）

A、F与l的积为定值 B、F随l的增大而减小 C、当l为 $1.5 m$ 时，撬动石头至少需要 $400 N$ 的力 D、F关于l的函数图象位于第一、第三象限

查看试题解析
10. 如图是4个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作T_m（m为1～4的整数），函数y＝ $\frac{k}{x}$ （x＞0）的图象为曲线L．若曲线L使得T₁～T₄ ，这些点分布在它的两侧，每侧各2个点，则k的取值范围是（）

A、8≤k≤12 B、8≤k＜12 C、8＜k≤12 D、8＜k＜12

查看试题解析

二、填空题（每题2分，共12分）

11. 已知函数 $y = x + 1$ 的图象与 $x$ 轴、 $y$ 轴分别交于点 $C$ 、 $B$ ，与双曲线 $y = \frac{k}{x}$ 交于点 $A$ 、 $D .$ 若 $A B + C D = B C$ ，则 $k$ 的值为．

查看试题解析
12. 在平面直角坐标系中，经过反比例函数 $y = \frac{k}{x}$ 图象上的点A（1，5）的直线 $y = - 2 x + b$ 与x轴，y轴分别交于点C，D，且与该反比例函数图象交于另一点B.则 $B C + A D =$ .

查看试题解析
13. 已知直线 $y = (a - 2 b) x$ 与双曲线 $y = \frac{3 b + a}{x}$ 相交于点 $(\frac{2}{3} ， - 2)$ ，那么它们的另一个交点坐标是.

查看试题解析
14. 为预防“新冠病毒”，学校对教室喷洒 $84$ 消毒液（含氯消毒剂）进行消杀，资料表明空气中氯含量不低于 $0.5 %$ ，才能有效杀灭新冠病毒．如图，喷洒消毒液时教室空气中的氯含量 $y (%)$ 与时间 $t (m i n)$ 成正比例，消毒液挥发时，y与t成反比例，则此次消杀的有效作用时间是min．

查看试题解析
15. 如图，一块砖的A，B，C三个面的面积之比是 $1 ： 5 ： 3$ ．如果A，B，C三个面分别向下放在地上，地面所受压强分别为 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ，压强的计算公式为 $P = \frac{F}{S}$ ，其中P是压强，F是压力，S是受力面积，则 $P_{1}$ ， $P_{2}$ ， $P_{3}$ 的大小关系为（用小于号连接）．

查看试题解析
16. 油箱注满 $k$ 升油后，轿车可行驶的总路程 $S$ (单位：千米)与平均耗油量 $a$ (单位：升/千米)之间是反比例函数关系 $S = \frac{k}{a}$ ( $k$ 是常数， $k \neq 0)$ .已知某轿车油箱注满油后，以平均耗油量为每千米0.1升的速度行驶，可行驶700千米.则该轿车可行驶的总路程 $S$ 与平均耗油量 $a$ 之间的函数关系式为.

查看试题解析

三、解答题（共10分，共88分）

17. 如图，一块砖的A，B，C三个面的面积比是 $4 ： 2 ： 1$ .如果B面向下放在地上，地面所受压强为 $a$ $P a$ ，那么A面和C面分别向下放在地上时，地面所受压强各是多少？

查看试题解析
18. 甲工程队新建公路，每名工人每天工作8小时，则甲工程队每天可完成600米新建公路．乙工程队比甲工程队少10名工人，每名工人每天工作10小时，则乙工程队每天可完成500米新建公路，假定甲、乙两工程队的每名工人每小时完成的工作量相同，求乙工程队的工人有多少名？

查看试题解析
19. 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．

(1)、求这个反比例函数的解析式，并直接写出蓄电池的电压值（单位：v）

(2)、如果以此蓄电池为电源的用电器的限制电流不能超过10A，那么用电器可变电阻应控制在什么范围？

查看试题解析
20. 在探究欧姆定律时，小明发现小灯泡电路上的电压保持不变，通过小灯泡的电流越大，灯就越亮.设选用小灯泡的电阻为 $R (Ω)$ ，通过的电流强度为 $I (A)$ .

(1)、若电阻为 $40 Ω$ ，通过的电流强度为 $0.30 A$ ，求I关于R的函数表达式.

(2)、如果电阻小于 $40 Ω$ ，那么与原来的相比，小灯泡的亮度将发生什么变化？

查看试题解析
21. 在直角坐标系中，设反比例函数 $y_{1} = \frac{k_{1}}{x} (k_{1} \neq 0)$ 与一次函数 $y_{2} = k_{2} x + b (k_{2} \neq 0)$ 的图象都经过点 $A$ 和点 $B$ ，点 $A$ 的坐标为 $(1 ， m)$ ，点 $B$ 的坐标为 $(- 2 ， - 2)$ ．

(1)、求 $m$ 的值和一次函数 $y_{2}$ 的表达式．

(2)、当 $y_{1} > y_{2}$ 时，直接写出 $x$ 的取值范围．

(3)、把函数 $y_{2}$ 的图象向下平移 $n (n > 0)$ 个单位后，与函数 $y_{1}$ 的图象交于点 $(p_{1} ， q_{1})$ 和 $(p_{2} ， q_{2})$ ，当 $p_{1} = - 1$ 时，求此时 $n$ 及 $p_{2} \times q_{2}$ 的值．

查看试题解析
22. 在面积都相等的所有矩形中，当其中一个矩形的一边长为1时，其邻边长为3.

(1)、设矩形的相邻两边长分别为x，y.
①求y关于工的函数表达式；

②当y≥3时，求x的取值范围.

(2)、圆圆说其中有一个矩形的周长为6，方方说有一个矩形的周长为10，你认为圆圆和方方的说法对吗?为什么?

查看试题解析
23. 《城镇污水处理厂污染物排放标准》中硫化物的排放标准为 $1.0 m g / L$ .某污水处理厂在自查中发现，所排污水中硫化物浓度超标，因此立即整改，并开始实时监测.据监测，整改开始第60小时时，所排污水中硫化物的浓度为 $5 m g / L$ ；从第60小时开始，所排污水中硫化物的浓度 $y (m g / L)$ 是监测时间x（小时）的反比例函数，其图象如图所示.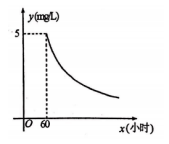

(1)、求y与x的函数关系式；

(2)、整改开始第100小时时，所排污水中硫化物浓度为 $m g / L$ ；

(3)、按规定所排污水中硫化物的浓度不超过 $0.8 m g / L$ 时，才能解除实时监测，此次整改实时监测的时间至少为多少小时？

查看试题解析
24. 如图1，将一长方体放置于一水平玻璃桌面上，按不同的方式摆放，记录桌面所受压强与受力面积的关系如下表所示：
桌面所受压强 $P (P a)$
400
500
800
1000
1250
受力面积 $S (m^{2})$
0.5
0.4
$a$
0.2
0.16

(1)、根据表中数据，求出压强 $P (P a)$ 关于受力面积 $S (m^{2})$ 的函数表达式及 $a$ 的值．

(2)、如图2，将另一长，宽，高分别为 $60 c m$ ， $20 c m$ ， $10 c m$ ，且与原长方体相同重量的长方体放置于该水平玻璃桌面上．若玻璃桌面能承受的最大压强为 $2000 P a$ ，问：这种摆放方式是否安全？请判断并说明理由．

查看试题解析
25. 长为 $300 m$ 的春游队伍，以 $v （ m / s ）$ 的速度向东行进，如图1和图2，当队伍排尾行进到位置O时，在排尾处的甲有一物品要送到排头，送到后立即返回排尾，甲的往返速度均为 $2 v （ m / s ）$ ，当甲返回排尾后，他及队伍均停止行进．设排尾从位置O开始行进的时间为 $t （ s ）$ ，排头与O的距离为 $S_{头} （ m ）．$

(1)、当 $v = 2$ 时，解答：
①求 $S_{头}$ 与t的函数关系式（不写t的取值范围）；
②当甲赶到排头位置时，求 $S_{头}$ 的值；在甲从排头返回到排尾过程中，设甲与位置O的距离为 $S_{甲} （ m ）$ ，求 $S_{甲}$ 与t的函数关系式（不写t的取值范围）

(2)、设甲这次往返队伍的总时间为 $T （ s ）$ ，求T与v的函数关系式（不写v的取值范围），并写出队伍在此过程中行进的路程．

查看试题解析
26. 模具厂计划生产面积为4，周长为m的矩形模具.对于m的取值范围，小亮已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：

(1)、建立函数模型
设矩形相邻两边的长分别为x，y，由矩形的面积为4，得 $x y = 4$ ，即 $y = \frac{4}{x}$ ；由周长为 $m$ ，得 $2 (x + y) = m$ ，即 $y =$ $- x + \frac{m}{2}$ .满足要求的 $(x ， y)$ 应是两个函数图象在第象限内交点的坐标.

(2)、画出函数图象
函数 $y = \frac{4}{x} (x > 0)$ 的图象如图所示，而函数 $y = - x + \frac{m}{2}$ 的图象可由直线 $y = - x$ 平移得到.请在同一直角坐标系中直接画出直线 $y = - x$ .

(3)、平移直线 $y = - x$ ，观察函数图象
①当直线平移到与函数 $y = \frac{4}{x} (x > 0)$ 的图象有唯一交点 $(2 ， 2)$ 时，周长 $m$ 的值为▲ ；

②在直线平移过程中，交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.

(4)、得出结论
若能生产出面积为4的矩形模具，则周长m的取值范围为.

查看试题解析

桌面所受压强 $P (P a)$	400	500	800	1000	1250
受力面积 $S (m^{2})$	0.5	0.4	$a$	0.2	0.16

浙教版数学八年级下学期期末复习常考题微专练： 反比例函数的应用

一、单选题（每题2分，共20分）

二、填空题（每题2分，共12分）

三、解答题（共10分，共88分）

浙教版数学八年级下学期期末复习常考题微专练：反比例函数的应用