浙教版数学八年级下学期期末复习常考题微专练:反比例函数的图象与性质
试卷更新日期:2023-05-13 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列函数中,表示y是x的反比例函数的是( )A、 B、 C、 D、2. 关于反比例函数 ,下列说法错误的是( )A、y随x的增大而减小 B、图象位于第一、三象限 C、图象过点(-1,-2) D、图象关于原点成中心对称3. 若反比例函数的图象经过点 , 则下列各点中,不在该函数图象上的是( )A、 B、 C、 D、4. 已知 是反比例函数,则函数的图象在( )A、第一、二象限 B、第三、四象限 C、第一、三象限 D、第二、四象限5. 已知点A(1,y1),B(2,y2),C(﹣3,y3)都在反比例函数y (k>0)的图象上,则y1 , y2 , y3的大小关系是( )A、y3<y1<y2 B、y1<y2<y3 C、y2<y1<y3 D、y3<y2<y16. 如图,点A是反比例函数y= (x>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣ 的图象于点B,以AB为边作▱ABCD,其中C、D在x轴上,则S▱ABCD为( )
 A、2.5 B、3 C、5 D、67. 如图,在矩形ABCO中,点D在BC边上,连结AD,把△ABD沿AD折叠,使点B恰好落在OC边上的点E处,已知B(10,8),反比例函数y= (k≠0)的图象经过点D,则k的值为( )
A、2.5 B、3 C、5 D、67. 如图,在矩形ABCO中,点D在BC边上,连结AD,把△ABD沿AD折叠,使点B恰好落在OC边上的点E处,已知B(10,8),反比例函数y= (k≠0)的图象经过点D,则k的值为( ) A、20 B、30 C、40 D、488. 若反比例函数的图象经过点(﹣1,3),则该反比例函数的表达式是( )A、 B、 C、y=﹣3x D、y=3x9. 已知y是关于x的反比例函数, , 和 , 是自变量与函数的两组对应值.则下列关系式中,成立的是( )A、 B、 C、 D、10. 若点A(a﹣1,y1),B(a+1,y2)是反比例函数y=﹣ 图象的两个点,且y1<y2 , 则a的取值范围是( )A、a<﹣1 B、﹣1<a<1 C、a>1 D、a<﹣1或a>1
A、20 B、30 C、40 D、488. 若反比例函数的图象经过点(﹣1,3),则该反比例函数的表达式是( )A、 B、 C、y=﹣3x D、y=3x9. 已知y是关于x的反比例函数, , 和 , 是自变量与函数的两组对应值.则下列关系式中,成立的是( )A、 B、 C、 D、10. 若点A(a﹣1,y1),B(a+1,y2)是反比例函数y=﹣ 图象的两个点,且y1<y2 , 则a的取值范围是( )A、a<﹣1 B、﹣1<a<1 C、a>1 D、a<﹣1或a>1二、填空题(每空3分,共18分)
-
11. 对于函数 ,当 时, 是 的反比例函数,且比例系数是3.12. 正比例函数与反比例函数的图象交于、两点,则代数式的值是.13. 已知反比例函数 , 当时,y的最大值与最小值之差是4,则k=.14. 如图,▱的边在轴上,顶点在反比例函数的图象上,与轴相交于点 , 且为的中点,则▱的面积为 .
 15. 如图,在平面直角坐标系 中,点A,B是反比例函数 ( ,k为常数)的图象上两点(点A在第一象限,点B在第三象限),线段 交x轴于点C,若 , 的面积分别为: 和 ,则k=.
15. 如图,在平面直角坐标系 中,点A,B是反比例函数 ( ,k为常数)的图象上两点(点A在第一象限,点B在第三象限),线段 交x轴于点C,若 , 的面积分别为: 和 ,则k=. 16. 反比例函数y=的图象与一次函数y=mx+n的图象交于两点(a,a-1),(a-7,-a),则不等式>mx+n的解集为
16. 反比例函数y=的图象与一次函数y=mx+n的图象交于两点(a,a-1),(a-7,-a),则不等式>mx+n的解集为三、解答题(共9题,共72分)
-
17. 已知函数 与 成正比例, 与 成反比例,且当 时, ;当 时, ,求 与 的函数关系式.18. 在平面直角坐标系中,反比例函数y=(x>0,k>0)的图象经过点A(m,n),B(2,1),且n>1,过点B作y轴的垂线,垂足为C,若△ABC的面积为2,求点A的坐标.
 19. 对于函数 , 小明根据学习一次函数和反比例函数的经验,研究了它的图象和性质.下面是小明的分析和研究过程,请补充完整.(1)、自变量x的取值范围是.(2)、根据列表计算的部分对应值,在平面直角坐标系中用描点法画出该函数的图象.
19. 对于函数 , 小明根据学习一次函数和反比例函数的经验,研究了它的图象和性质.下面是小明的分析和研究过程,请补充完整.(1)、自变量x的取值范围是.(2)、根据列表计算的部分对应值,在平面直角坐标系中用描点法画出该函数的图象.x
0
1
3
4
5
y
-6
6
3
2
 (3)、从中心对称和轴对称的角度分析图象特征,并说说这个函数的增减性.20. 如图,在平面直角坐标系中,O是坐标原点,反比例函数y1= 的图象与正比例函数y2=2x的图象交于A,B两点,点C在x轴正半轴上,AC=AO,△ACO的面积为8.
(3)、从中心对称和轴对称的角度分析图象特征,并说说这个函数的增减性.20. 如图,在平面直角坐标系中,O是坐标原点,反比例函数y1= 的图象与正比例函数y2=2x的图象交于A,B两点,点C在x轴正半轴上,AC=AO,△ACO的面积为8.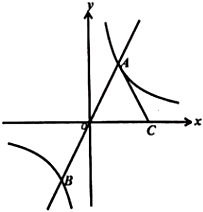 (1)、求k的值和B点的坐标;(2)、根据图象直接写出y1>y2时x的取值范围.21. 如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于A,BC⊥y轴于C,BA=3,BC=5,有一反比例函数图象刚好过点B.
(1)、求k的值和B点的坐标;(2)、根据图象直接写出y1>y2时x的取值范围.21. 如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于A,BC⊥y轴于C,BA=3,BC=5,有一反比例函数图象刚好过点B.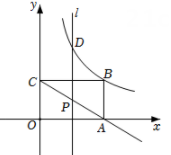 (1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.22. 已知点 , 都在反比例函数的图象上.(1)、当时.
(1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.22. 已知点 , 都在反比例函数的图象上.(1)、当时.①求反比例函数表达式,并求出点的坐标;
②当时,求的取值范围;
(2)、若一次函数与轴交于点 , 求的值.23. 背景:点在反比例函数的图象上,轴于点 , 轴于点 , 分别在射线 , 上取点 , , 使得四边形为正方形,如图 , 点在第一象限内,当时,小李测得 .探究:通过改变点的位置,小李发现点 , 的横坐标之间存在函数关系.请帮助小李解决下列问题.
 (1)、求的值.(2)、设点 , 的横坐标分别为 , , 将关于的函数称为“函数”,如图2,小李画出了时“函数”的图象.
(1)、求的值.(2)、设点 , 的横坐标分别为 , , 将关于的函数称为“函数”,如图2,小李画出了时“函数”的图象.求这个“函数”的表达式.
补画时“函数”的图象,并写出这个函数的性质两条即可 .
24. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长米,另一边长加长米,可得与之间的函数关系式某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数 , 现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整: (1)、类比反比例函数可知,函数的自变量的取值范围是 , 这个函数值的取值范围是 .(2)、“数学兴趣小组”进一步思考函数的图象和性质,请根据函数的图象,画出函数的图象;(3)、结合函数的图象解答下列问题:
(1)、类比反比例函数可知,函数的自变量的取值范围是 , 这个函数值的取值范围是 .(2)、“数学兴趣小组”进一步思考函数的图象和性质,请根据函数的图象,画出函数的图象;(3)、结合函数的图象解答下列问题:①求出方程的根;
②如果方程有2个实数根,请直接写出的取值范围.
25. 阅读理解:【材料一】若三个非零实数x,y,z中有一个数的平方等于另外两个数的积,则称三个实数x,y,z构成“友好数”.
【材料二】若关于x的一元二次方程的两根分别为 , 则有: .
问题解决:
(1)、实数4,6,9可以构成“友好数”吗?请说明理由;(2)、若三点均在函数(k为常数且)的图象上,且这三点的纵坐标构成“友好数”,求实数t的值;(3)、设三个实数是“友好数”且满足 , 其中是关于x的一元二次方程的两个根,是抛物线与x轴的一个交点的横坐标.①的值等于 ;
②设 , 求y关于x的函数关系式.