浙教版数学八年级下学期期末复习常考题微专练:菱形
试卷更新日期:2023-05-13 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 菱形不一定具有的性质是( )A、对角线互相平分 B、是轴对称图形 C、对角线相等 D、对角线互相垂直2. 已知在菱形中, , , 则菱形的面积为( )
 A、160 B、80 C、40 D、963. 如图,菱形ABCD的顶点A;B分别在y轴正半轴,x轴正半轴上,点C的横坐标为10,点D的纵坐标为8,若直线AC平行x轴,则菱形ABCD的边长值为( )
A、160 B、80 C、40 D、963. 如图,菱形ABCD的顶点A;B分别在y轴正半轴,x轴正半轴上,点C的横坐标为10,点D的纵坐标为8,若直线AC平行x轴,则菱形ABCD的边长值为( ) A、9 B、 C、6 D、34. 如图添加下列一个条件,能使平行四边形ABCD成为菱形的是( )
A、9 B、 C、6 D、34. 如图添加下列一个条件,能使平行四边形ABCD成为菱形的是( )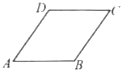 A、AB=CD B、AC=BD C、∠BAD=90° D、AB=BC5. 已知 , 用没有刻度的直尺和圆规作菱形 , 下面的作法中正确的是( )A、
A、AB=CD B、AC=BD C、∠BAD=90° D、AB=BC5. 已知 , 用没有刻度的直尺和圆规作菱形 , 下面的作法中正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,甲、乙是两张不同的平行四边形纸片,将它们分别沿着虚线剪开后,各自要拼接一个与原来面积相等的菱形,则( )
6. 如图,甲、乙是两张不同的平行四边形纸片,将它们分别沿着虚线剪开后,各自要拼接一个与原来面积相等的菱形,则( ) A、甲、乙都可以 B、甲可以,乙不可以 C、甲、乙都不可以 D、甲不可以,乙可以7. 如图,边长为10的菱形ABCD,E是AD的中点,O是对角线的交点,矩形OEFG的一边在AB上,且EF=4,则BG的长为( )
A、甲、乙都可以 B、甲可以,乙不可以 C、甲、乙都不可以 D、甲不可以,乙可以7. 如图,边长为10的菱形ABCD,E是AD的中点,O是对角线的交点,矩形OEFG的一边在AB上,且EF=4,则BG的长为( ) A、3 B、2 C、 D、18. 如图,平行四边形 的对角线交于点 点 、 分别是边 , 的中点,连接 , 下列结论: 若四边形 是菱形,则 ; 若四边形 是矩形,则 ; 若 ,则四边形 是矩形; 若 ,则四边形 是菱形.其中正确的是( )
A、3 B、2 C、 D、18. 如图,平行四边形 的对角线交于点 点 、 分别是边 , 的中点,连接 , 下列结论: 若四边形 是菱形,则 ; 若四边形 是矩形,则 ; 若 ,则四边形 是矩形; 若 ,则四边形 是菱形.其中正确的是( ) A、 B、 C、 D、9. 如图1,在菱形ABCD中,对角线AC、BD相交于O,要在对角线BD上找两点M、N,使得四边形AMCN是菱形,现有图2中的甲、乙两种方案,则正确的方案是( )
A、 B、 C、 D、9. 如图1,在菱形ABCD中,对角线AC、BD相交于O,要在对角线BD上找两点M、N,使得四边形AMCN是菱形,现有图2中的甲、乙两种方案,则正确的方案是( ) A、只有甲 B、只有乙 C、甲和乙 D、甲乙都不是10. 如图,菱形ABCD的边长为 .顺次连结菱形ABCD各边中点,可得四边形 ;顺次连结四边形 各边中点,可得四边形 ;顺次连结四边形 各边中点,可得四边形 ;按此规律继续下去,四边形 的周长是( )
A、只有甲 B、只有乙 C、甲和乙 D、甲乙都不是10. 如图,菱形ABCD的边长为 .顺次连结菱形ABCD各边中点,可得四边形 ;顺次连结四边形 各边中点,可得四边形 ;顺次连结四边形 各边中点,可得四边形 ;按此规律继续下去,四边形 的周长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共24分)
-
11. 如图,已知点E,F分别是▱ABCD的边BC,AD上的中点,且∠BAC=90°,若∠B=30°,BC=10,则四边形AECF的面积为.
 12. 如图,以菱形的顶点A为圆心,长为半径画弧,交对角线于点E.若 , , 则菱形的周长为.
12. 如图,以菱形的顶点A为圆心,长为半径画弧,交对角线于点E.若 , , 则菱形的周长为. 13. 小明同学学习了菱形的知识后,结合之前学习的赵爽弦图,编了一个菱形版“赵爽弦图”如图,菱形中, , 四边形是矩形,若 , 则矩形的面积为 .
13. 小明同学学习了菱形的知识后,结合之前学习的赵爽弦图,编了一个菱形版“赵爽弦图”如图,菱形中, , 四边形是矩形,若 , 则矩形的面积为 . 14. 如图,有两张矩形纸片ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.将两纸片按如图所示叠放,使点D与点G重合,且重叠部分为平行四边形.当两张纸片交叉所成的角记为α,当α=30°时,BM=;当α最小时,重叠部分的面积为 .
14. 如图,有两张矩形纸片ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.将两纸片按如图所示叠放,使点D与点G重合,且重叠部分为平行四边形.当两张纸片交叉所成的角记为α,当α=30°时,BM=;当α最小时,重叠部分的面积为 .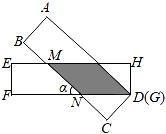 15. 如图,矩形ABCD(AD>AB),分别以AD,BC为边向内作等边三角形(图1);分别以AB,CD为边向内作等边三角形(图2),两个等边三角形的重叠部分用阴影部分表示,设图1中阴影部分面积为S1 , 图2中阴影部分的面积为S2 , 若 , 则的值为.
15. 如图,矩形ABCD(AD>AB),分别以AD,BC为边向内作等边三角形(图1);分别以AB,CD为边向内作等边三角形(图2),两个等边三角形的重叠部分用阴影部分表示,设图1中阴影部分面积为S1 , 图2中阴影部分的面积为S2 , 若 , 则的值为. 16. 如图,在菱形ABCD中,AB=8,∠BAD=60°.在其内部作形状、大小都相同的菱形AENH和菱形CGMF,使点E,F,G,H分别在边AB,BC,CD,DA上,点M,N在对角线AC上,
16. 如图,在菱形ABCD中,AB=8,∠BAD=60°.在其内部作形状、大小都相同的菱形AENH和菱形CGMF,使点E,F,G,H分别在边AB,BC,CD,DA上,点M,N在对角线AC上, (1)、若AE=3BE,则MN的长为(2)、若AE=BE, 点P、Q分别是DE、AD上的两个动点,则AP+PQ的最小值是 .
(1)、若AE=3BE,则MN的长为(2)、若AE=BE, 点P、Q分别是DE、AD上的两个动点,则AP+PQ的最小值是 .三、综合题
-
17. 如图,已知等腰三角形ABD,把它沿底边BD翻折,得到△CBD.求证:四边形ABCD是菱形.
 18. 如图,菱形 中, 为对角线 的延长线上一点.求证:
18. 如图,菱形 中, 为对角线 的延长线上一点.求证: 19. 如图所示,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB,BC,CD,DA 的中点分别为P,Q,M ,N,试判断四边形 PQMN为怎样的四边形,并证明你的结论.
19. 如图所示,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB,BC,CD,DA 的中点分别为P,Q,M ,N,试判断四边形 PQMN为怎样的四边形,并证明你的结论. 20. 如图,在矩形ABCD中,点E,F分别在AD,BC上,且AE=CF.
20. 如图,在矩形ABCD中,点E,F分别在AD,BC上,且AE=CF. (1)、求证:四边形BFDE是平行四边形:(2)、若AB=2,AD=4,四边形BFDE是菱形,求AE长.21. 如图,矩形中,对角线 , 交于点 , 过点作的平行线,过点作的平行线,这两条平行线交于点 .
(1)、求证:四边形BFDE是平行四边形:(2)、若AB=2,AD=4,四边形BFDE是菱形,求AE长.21. 如图,矩形中,对角线 , 交于点 , 过点作的平行线,过点作的平行线,这两条平行线交于点 .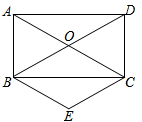 (1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.22. 如图,平行四边形 , , E、F分别是边上的两个动点,且满足 .
(1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.22. 如图,平行四边形 , , E、F分别是边上的两个动点,且满足 . (1)、求证:;(2)、判断的形状,并说明理由.(3)、的周长是否存在最小值,若存在,请直接写出周长的最小值;若不存在,请说明理由.23. 如图,已知菱形 , ,点 是射线 上的动点,以 为边向右侧作等边 ,连结 .
(1)、求证:;(2)、判断的形状,并说明理由.(3)、的周长是否存在最小值,若存在,请直接写出周长的最小值;若不存在,请说明理由.23. 如图,已知菱形 , ,点 是射线 上的动点,以 为边向右侧作等边 ,连结 .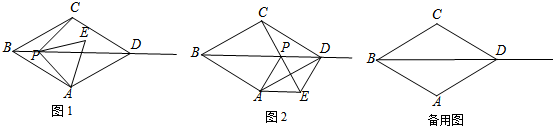 (1)、如图1,点 在线段 上,求证: .(2)、如图2,当 , , 三点共线时,连结 ,求证:四边形 是菱形.(3)、当 时,求 的值.24. 如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于A,BC⊥y轴于C,BA=3,BC=5,有一反比例函数图象刚好过点B.
(1)、如图1,点 在线段 上,求证: .(2)、如图2,当 , , 三点共线时,连结 ,求证:四边形 是菱形.(3)、当 时,求 的值.24. 如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于A,BC⊥y轴于C,BA=3,BC=5,有一反比例函数图象刚好过点B.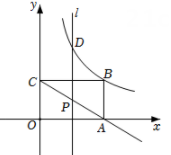 (1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、分别求出过点B的反比例函数和过A,C两点的一次函数的表达式.(2)、动点P在射线CA(不包括C点)上,过点P作直线l⊥x轴,交反比例函数图象于点D.是否存在这样的点Q,使得以点B,D,P,Q为顶点的四边形为菱形?若存在,求出点Q的坐标;若不存在,请说明理由.