浙教版数学七年级下学期期末复习常考题微专练：分式方程

试卷更新日期：2023-05-13 类型：复习试卷

进入出卷网下载

一、单选题（每题2分，共20分）

1. 下列关于 $x$ 的方程① $\frac{x - 1}{3} = 5$ ，② $\frac{1}{x} = \frac{4}{x - 1}$ ，③ $\frac{3 - x}{3} = x - 1$ ，④ $\frac{x}{a} = \frac{1}{b - 1}$ 中，是分式方程的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 解分式方程 $\frac{2 x}{x - 1} - \frac{x - 2}{1 - x} = \frac{1}{2}$ 时，去分母后得到的方程正确的是（）

A、 $2 x - (x - 2) = x - 1$ B、 $4 x - 2 (x - 2) = x - 1$ C、 $4 x + 2 (x - 2) = x - 1$ D、 $2 x + (x - 2) = x - 1$

查看试题解析
3. 下列解分式方程 $\frac{x}{x - 2} + \frac{2}{2 - x} = 0$ 的步骤中，错误的是（）

A、找最简公分母：2-x B、去分母： $- x + 2 = 0$ C、计算方程的根： $x = 2$ D、验根：当 $x = 2$ 时，方程 $\frac{x}{x - 2} + \frac{2}{2 - x} = 0$ 成立

查看试题解析
4. 已知关于x的分式 $\frac{x - a}{x - 2} + \frac{2 a}{2 - x} = 2$ 的解为非负数，则a的范围为（）

A、 $a \leq \frac{4}{3}$ 且 $a \neq \frac{2}{3}$ B、 $a \geq \frac{2}{3}$ 且 $a \neq \frac{4}{3}$ C、 $a \leq - \frac{1}{3}$ 且 $a \neq - \frac{2}{3}$ D、 $a \geq \frac{1}{3}$ 且 $a \neq \frac{2}{3}$

查看试题解析
5. 已知关于x的分式方程 $\frac{x + m}{x - 3}$ ﹣1＝ $\frac{1}{x}$ 无解，则m的值是（）；

A、﹣2 B、﹣3 C、﹣2或﹣3 D、0或3

查看试题解析
6. 若关于x的方程 $\frac{x}{x - 3} + \frac{3 a}{3 - x} =$ 3a有增根，则a的值为（）

A、﹣l B、 $\frac{1}{7}$ C、 $\frac{1}{3}$ D、1

查看试题解析
7. 设m，n为实数，定义如下一种新运算：m☆n = $\frac{n}{3 m - 9}$ ，若关于x的方程a（x☆x）=（x☆12）+1无解，则a的值是（）

A、4 B、﹣3 C、4或﹣3 D、4或3

查看试题解析
8. 某工程队承接了60万平方米的绿化工程，由于情况有变， $\dots .$ 设原计划每天绿化的面积为 $x$ 万平方米，列方程为 $\frac{60}{(1 - 20 %) x} - \frac{60}{x} = 30$ ，根据方程可知省略的部分是（）

A、实际工作时每天的工作效率比原计划提高了20%，结果提前30天完成了这一任务 B、实际工作时每天的工作效率比原计划提高了20%，结果延误30天完成了这一任务 C、实际工作时每天的工作效率比原计划降低了20%，结果延误30天完成了这一任务 D、实际工作时每天的工作效率比原计划降低了20%，结果提前30天完成了这一任务

查看试题解析
9. 某市政工程队准备修建一条长1200米的污水处理管道.在修建完400米后，为了能赶在汛期前完成，采用新技术，工作效率比原来提升了25%.结果比原计划提前4天完成任务.设原计划每天修建管道x米，依题意列方程得（）

A、 $\frac{1200}{x} - \frac{1200}{x (1 + 25 %)} = 4$ B、 $\frac{1200 - 400}{x} - \frac{1200 - 400}{x (1 + 25 %)} = 4$ C、 $\frac{1200}{x} - \frac{1200 - 400}{x (1 + 25 %)} = 4$ D、 $\frac{1200 - 400}{x (1 + 25 %)} - \frac{1200 - 400}{x} = 4$

查看试题解析
10. 甲、乙、丙三名工人共承担装搭一批零件.已知甲乙丙丁四人聊天时的对话信息如下：
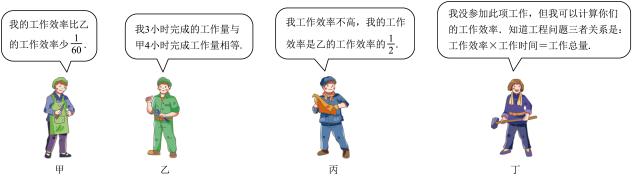
如果每小时只安排1名工人，那么按照甲、乙、丙的轮流顺序至完成工作任务，共需（）小时.

A、20 B、21 C、19 $\frac{1}{4}$ D、19 $\frac{3}{4}$

查看试题解析

二、填空题（每空3分，共21分）

11. 若方程 $\frac{2}{1 - x} = \frac{x}{x - 1} - 3$ 的解为 $x = \frac{5}{2}$ ，则方程 $\frac{2}{1 - 2 y} = \frac{2 y}{2 y - 1} - 3$ 的解为 $y =$ ．

查看试题解析
12. 当 $x =$ 时.代数式 $\frac{x - 5}{x - 8}$ 和 $\frac{4 - 2 x}{8 - x}$ 的值互为相反数

查看试题解析
13. 若分式方程 $\frac{a}{x + 2}$ ＝4﹣ $\frac{2}{x + 2}$ 无解，则a的值为.

查看试题解析
14. 某感冒药用来计算儿童服药量 $y$ 的公式为 $y = \frac{a x}{x + 12}$ ，其中 $a$ 为成人服药量， $x$ 为儿童的年龄 $(x \leq 13)$ ，如果一个儿童的服药量恰好是成人服药量的 $\frac{1}{3}$ ，那么他的年龄是岁 $.$

查看试题解析
15. $m + n$ ， $\frac{1}{m} + \frac{1}{n}$ ， $m^{2} + n^{2}$ 等代数式，如果交换m和n的位置，式子的值不变，我们把这样的式子叫做完美对称式. 若关于x，y的分式 $\frac{y}{x} - \frac{m x}{y}$ 是完美对称式，则： $m =$ ；若完美对称式 $\frac{y}{x} - \frac{m x}{y}$ 满足： $\frac{y}{x} - \frac{m x}{y} = x y + 2$ ，且 $x > y > 0$ ，则 $y =$ （用含x的代数式表示）.

查看试题解析
16. 对于两个不相等的实数a，b，我们规定符号min{a，b'表示a，b中的较小的值，如min{2，4}=2，按㸛这个规定，当 $x > 0$ 时，方程 $\min {\frac{5}{x} ， \frac{2}{x}} =$ $\frac{6}{x} - 2$ 的解为.

查看试题解析

三、计算题（共12分）

17. 解分式方程.

(1)、 $\frac{2}{x + 3} = \frac{5}{x}$ ；

(2)、 $\frac{x}{2 x - 5} - 1 = \frac{5}{5 - 2 x}$ ；

(3)、 $\frac{1}{x - 4} = \frac{4}{x^{2} - 16}$ ；

(4)、 $5 + \frac{88}{x^{2} - 16} = \frac{2 x - 1}{x + 4} - \frac{3 x - 1}{4 - x}$

查看试题解析

四、解答题（共8题，共67分）

18. 以下是琦琦同学解《作业本》中的一个分式方程
$\frac{5 - x}{x - 4} + \frac{1}{4 - x} = 1$ 的解答过程.

解：去分母，得 $5 - x - 1 = 1$ ，

移项，合并同类项，得 $x = 3$ ，

检验：将 $x = 3$ 代入最简公分母 $x - 4 = 3 - 4 = - 1 \neq 0$ ，

∴ $x = 3$ 是原方程的根.

琦琦的解答过程对吗?如果不对，请写出正确的解答过程.

查看试题解析
19. 第5代移动通信技术简称5G，某地已开通5G业务，经测试5G下载速度是4G下载速度的10倍，小明和小颖分别用5G与4G下载一部900兆的公益片，小明比小颖所用的时间快162秒，该地4G与5G的下载速度分别是每秒多少兆?

查看试题解析
20. 嵊州榨面是嵊州美食的一张名片，某面馆推出两款经典美食榨面，一款是色香味俱全的“炒榨面”，另一款是清香四溢的“汤水榨面”．已知2份“炒榨面”和1份“汤水榨面”需46元；1份“炒榨面”和2份“汤水榨面”需38元．

(1)、求“炒榨面”、“汤水榨面”的单价．

(2)、鸭蛋是两款美食必不可少的配料，该面馆老板发现本月的每千克鸭蛋价格比上个月涨了25%，同样花160元买到的鸭蛋数量比上个月少了2千克，求本月鸭蛋的价格．

查看试题解析
21. 我们把形如 $x + \frac{a b}{x} = a + b (a ， b$ 不为零 $)$ ，且两个解分别为 $x_{1} = a$ ， $x_{2} = b$ 的方程称为“十字分式方程”.
例如 $x + \frac{3}{x} = 4$ 为十字分式方程，可化为 $x + \frac{1 \times 3}{x} = 1 + 3$ ， $∴ x_{1} = 1$ ， $x_{2} = 3$ .

再如 $x + \frac{8}{x} = - 6$ 为十字分式方程，可化为 $x + \frac{(- 2) \times (- 4)}{x} = (- 2) + (- 4)$ ， $∴ x_{1} = - 2$ ， $x_{2} = - 4$ .

应用上面的结论解答下列问题：

(1)、若 $x + \frac{6}{x} = - 5$ 为十字分式方程，则 $x_{1} =$ ， $x_{2} =$ .

(2)、若十字分式方程 $x - \frac{5}{x} = - 2$ 的两个解分别为 $x_{1} = m$ ， $x_{2} = n$ ，求 $\frac{n}{m} + \frac{m}{n}$ 的值.

(3)、若关于 $x$ 的十字分式方程 $x - \frac{2 k^{2} + 3 k}{x - 2} = - k - 1$ 的两个解分别为 $x_{1}$ ， $x_{2} (k > 0 ， x_{1} > x_{2})$ ，求 $\frac{x_{1} - 2}{x_{2} + 1}$ 的值.

查看试题解析
22. 阅读下面材料，解答问题.
解方程： $\frac{x - 1}{x} - \frac{4 x}{x - 1} = 0$ .

解：设 $y = \frac{x - 1}{x}$ ，则原方程化为 $y - \frac{4}{y} = 0$ .

方程两边同时乘 $y$ ，得 $y^{2} - 4 = 0$ ，

解得 $y = \pm 2$ .

经检验 $y = \pm 2$ 都是方程 $y - \frac{4}{y} = 0$ 的根.

∴当 $y = 2$ 时， $\frac{x - 1}{x} = 2$ ，觕得 $x = - 1$ ；

当 $y = - 2$ 时， $\frac{x - 1}{x} = - 2$ ，解得 $x = \frac{1}{3}$ .

经检噞 $x = - 1$ 或 $x = \frac{1}{3}$ 都是原分式方程的偨，

∴原分式堭的根为 $x = - 1$ 或 $x = \frac{1}{3}$ .

上述这种解分式方程的方法称为换元法.问题：

(1)、若在方程 $\frac{x - 1}{4 x} - \frac{x}{x - 1} = 0$ 中，设 $y = \frac{x - 1}{x}$ ，则原为程可化为.

(2)、若在方程 $\frac{x - 1}{x + 1} - \frac{4 x + 4}{x - 1} = 0$ 中，设 $y = \frac{x - 1}{x + 1}$ ，则原方䅜可化为.

(3)、利用上述换元法解方程 $\frac{x - 1}{x + 2} - \frac{3}{x - 1} - 1 = 0$ .

查看试题解析
23. 对x，y定义一种新运算 $T$ ，规定： $T (x ， y) =$ $\frac{a x + b y}{2 x + y}$ (其中a，b均为非零常数)，这里等式右边是通常的四则运算.例如： $T (0 ， 1) = \frac{a \times 0 + b \times 1}{2 \times 0 + 1} =$ b.已知 $T (1 ， - 1) = - 2 ， T (4 ， 2) = 1$ .

(1)、求a，b

(2)、若T(m，m+3)=-1，求 $m$ 的值.

查看试题解析
24. 刘峰和李明相约周末去野生动物园游玩，根据他们的谈话内容，求李明乘公交车、刘峰骑自行车每小时各行多少千米？

查看试题解析
25. 化学实验室一容器内的a克盐水中含盐b克(盐水的浓度= $\frac{含盐质量}{盐水质量} \times 100 %$ )

(1)、若加入4克盐，食盐水的浓度怎么变化?为什么?（用数学的方法书写过程)

(2)、若a=50，b=5，加多少克盐可使该容器内的盐水浓度提高到原来的2倍?

(3)、若a=50，b=5，则需要蒸发多少克水，才使该容器内的盐水浓度提高到原来的2倍?

查看试题解析