浙教版数学七年级下学期期末复习常考题微专练：分式的运算

试卷更新日期：2023-05-13 类型：复习试卷

进入出卷网下载

一、单选题（每题2分，共20分）

1. 下列运算正确的是（）

A、 ${(\frac{a}{b})}^{2} = \frac{a^{2}}{b}$ B、 $\frac{- x - y}{x - y} = - 1$ C、 $\frac{1}{a} + \frac{1}{b} = \frac{2}{a + b}$ D、 $a^{3} \div \frac{1}{a} = a^{4}$

查看试题解析
2. 下列运算正确的是（）

A、 $\frac{1}{2 a} + \frac{1}{a} = \frac{2}{3 a}$ B、 $\frac{1}{a - 1} - \frac{1}{a + 1} = \frac{2}{a^{2} - 1}$ C、 $\frac{3 b}{4 a} \cdot \frac{2 a}{9 b^{2}} = \frac{b}{6}$ D、 $\frac{1}{3 a b} \div \frac{2 b^{2}}{3 a} = \frac{b^{3}}{2}$

查看试题解析
3. 已知 $\frac{1}{x} + \frac{1}{y + z} = \frac{1}{2}$ ， $\frac{1}{y} + \frac{1}{z + x} = \frac{1}{3}$ ， $\frac{1}{z} + \frac{1}{x + y} = \frac{1}{4}$ ，则 $\frac{2}{x} + \frac{3}{y} + \frac{4}{z}$ 的值为（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
4. 下列各选项中，所求的最简公分母错误的是（）

A、 $\frac{1}{3 x}$ 与 $\frac{1}{6 x}$ 的最简公分母是6x B、 $\frac{1}{3 a^{2} b^{3}}$ 与 $\frac{1}{3 a^{2} b^{3} c}$ 的最简公分母是 $3 a^{2} b^{3} c$ C、 $\frac{1}{a (x - y)}$ 与 $\frac{1}{b (y - x)}$ 的最简公分母是 $a b (x - y) (y - x)$ D、 $\frac{1}{m + n}$ 与 $\frac{1}{m - n}$ 的是简公分母是 $m^{2} - n^{2}$

查看试题解析
5. 下列选项中正确的是（）

A、分式 $\frac{y}{5 x^{2}}$ 和 $\frac{y}{2 x^{5}}$ 的最简公分母是 $10 x^{7}$ B、 $\frac{a}{b} = \frac{a c}{b c}$ C、 $\frac{a k}{b k} = \frac{a}{b}$ D、分式 $\frac{a^{2}}{a + b}$ 中的a，b同时扩大2倍，分式值不变

查看试题解析
6. 若 $a$ ， $b$ 为实数且满足 $a \neq - 1$ ， $b \neq - 1$ ，设 $M = \frac{a}{a + 1} + \frac{b}{b + 1}$ ， $N = \frac{1}{a + 1} + \frac{1}{b + 1}$ ，有以下2个结论： $①$ 若 $a b = l$ ，则 $M = N$ ； $②$ 若 $a + b = 0$ ，则 $M N \leq 0 .$ 下列判断正确的是（）

A、①对②错 B、①错②对 C、①②都错 D、①②都对

查看试题解析
7. 当分式 $- \frac{1}{x y}$ 与 $- \frac{1}{x^{2} y}$ 经过计算后的结果是 $- \frac{x + 1}{x^{2} y}$ 时，则它们进行的运算是（）

A、分式的加法 B、分式的减法 C、分式的乘法 D、分式的除法

查看试题解析
8. 若 $(\frac{4}{a^{2} - 4} + \frac{1}{2 - a}) \cdot w = 1$ ，则 $w =$ （）

A、 $a + 2 (a \neq - 2)$ B、 $- a + 2 (a \neq 2)$ C、 $a - 2 (a \neq 2)$ D、 $- a - 2 (a \neq \pm 2)$

查看试题解析
9. 如果 $m^{2} - 2 m - 2 = 0$ ，那么代数式 $(m - \frac{4 m - 4}{m})$ . $\frac{m^{2}}{2 - m}$ 的值是（）

A、-2 B、-1 C、2 D、3

查看试题解析
10. 已知实数a，b，c满足 $a + b = a b = c$ ，有下列结论： $①$ 若 $c = 5$ ，则 $a^{2} + b^{2} = 15$ ； $②$ 若 $a = 3$ ，则 $b + c = 9$ ； $③$ 若 $c \neq 0$ ，则 $\frac{a - 3 a b + b}{2 a + 7 a b + 2 b} = - \frac{2}{9}$ ； $④$ 若 $c \neq 0$ ，则 $(1 - a) (1 - b) = \frac{1}{a} + \frac{1}{b}$ ，其中结论正确的有（）

A、 $① ③$ B、 $① ② ④$ C、 $① ② ③$ D、 $① ③ ④$

查看试题解析

二、填空题（每空2分，共18分）

11. 计算：9a²· $\frac{b^{2}}{3 a}$ =

查看试题解析
12. $\frac{2}{3 x^{2} (x - y)}$ ， $\frac{1}{2 x - 2 y}$ 的公分母是.

查看试题解析
13. 若 $\frac{1}{x} + \frac{2}{y} + \frac{3}{z} = 5$ ， $\frac{3}{x} + \frac{2}{y} + \frac{1}{z} = 7$ ，则 $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} =$ .

查看试题解析
14. 已知两个非零实数a，b满足 $a^{2} + a = b + 3$ ， $b^{2} + b = a + 3$ ，则代数式 $\frac{b}{a} + \frac{a}{b}$ 的值为．

查看试题解析
15. 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行下一步计算，再将结果传递给下一人，最后完成化简.过程如图所示：

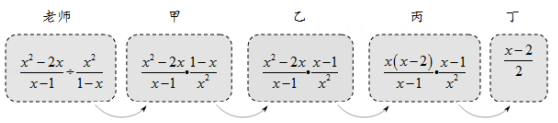
接力中，自己负责的一步出现错误的是.

查看试题解析
16. 如 $M = {1 ， 2 ， x}$ ，我们叫集合M．其中1，2，x叫做集合M的元素，集合中的元素具有确定性（如x必然存在），互异性（如 $x \neq 1$ ， $x \neq 2$ ），无序性（即改变元素的顺序，集合不变）．若集合 $N = {x ， 1 ， 2}$ ，我们说 $M = N$ ．已知集合 $A = {1 ， 0 ， a}$ ，集合 $B = {\frac{1}{a} ， | a | ， \frac{b}{a}}$ ，若 $A = B$ ，则 $b - a$ 的值是．

查看试题解析

三、计算题（共4题，共32分）

17. 计算.

(1)、 $\frac{4 x}{3 y} \cdot \frac{y}{2 x^{3}}$ .

(2)、 $\frac{x^{2}}{x^{2} - 1} \div \frac{x}{x - 1}$ .

(3)、 $\frac{9 a b^{2}}{a^{2} - b^{2}} \cdot \frac{5 a - 5 b}{3 a^{2} b}$ .

(4)、 $\frac{x^{2} - y^{2}}{4 x^{2} + 12 x y} \div \frac{x - y}{x + 3 y}$ .

(5)、 $\frac{- 3}{2 x - 4} \div \frac{1}{x - 2} \cdot \frac{x^{2} - 4}{x^{2} + 4 x + 4}$ .

查看试题解析
18. 计算.

(1)、 $\frac{1}{x} - \frac{x}{x + 1} - \frac{x}{x^{2} + x}$ ；

(2)、 $\frac{x^{2} - 4 x + 4}{x^{2} - 4} + \frac{x - 2}{x^{2} + 2 x} + 2$ ；

(3)、 $x + 2 y + \frac{4 y^{2}}{x - 2 y} - \frac{4 x^{2} y}{x^{2} - 4 y^{2}}$ .

查看试题解析
19. 计算： $(\frac{1}{a + b} + \frac{1}{a - b} - \frac{1}{a^{2} - b^{2}}) \div \frac{1}{a^{2} - b^{2}}$ .

查看试题解析
20. 化简： $\frac{1}{x (x + 1)} + \frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} +$ $\frac{1}{(x + 3) (x + 4)}$ .

查看试题解析

四、解答题（共6题，共50分）

21. 设代数式 $M = (\frac{4}{x^{2} - 4} + \frac{1}{2 - x}) \div \frac{x - 1}{3 x + 6}$ ．

(1)、化简 $M$ ；

(2)、从 $- 2$ ， 0，1，2中选择一个合适的数代入，求 $M$ 的值．

查看试题解析
22. 阅读下列计筫过程，回答问题：
解： $\frac{x - 3}{x^{2} - 1} - \frac{3}{1 - x} = \frac{x - 3}{(x + 1) (x - 1)} - \frac{3}{x - 1} \dots \dots$ ①

$= \frac{x - 3}{(x + 1) (x - 1)} - \frac{3 (x + 1)}{(x + 1) (x - 1)}$ ②

$= x - 3 - 3 (x + 1) \dots \dots$ ③

$= - 2 x - 6$ ④

(1)、上述计算过程中，从第步开始出现错误；

(2)、从第②步到第③步是否正确?答：(填“是”或“否”)；

(3)、请你写出正确的解答过程.

查看试题解析
23. 如果一个分式的分子或分母可以因式分解，且这个分式不可约分，那么我们称这个分式为“和谐分式”.

(1)、辨析：下列分式中，是和谐分式（填写序号即可）；
① $\frac{a^{2} + b^{2}}{(a + b)^{2}}$ ；② $\frac{t - 2 b}{t^{2} - 4 b^{2}}$ ；③ $\frac{x + y}{x^{2} - y^{2}}$ ；④ $\frac{m^{2} - 1}{m^{2} + 1}$ .

(2)、理解：若a为整数，且 $\frac{y - 1}{y^{2} + a y + 4}$ 为和谐分式，请写出a的值；

(3)、应用：先化简 $\frac{3 x + 6}{x + 1} - \frac{x - 1}{x} \div \frac{x^{2} - 1}{x^{2} + 2 x}$ ，并求x取什么整数时，该式的值为整数？

查看试题解析
24. 观察下列各式： $(x \neq 0)$
$(\frac{1}{x} - 1) (\frac{1}{x} + 1) = \frac{1}{x^{2}} - 1$ ，
$(\frac{1}{x} - 1) (\frac{1}{x^{2}} + \frac{1}{x} + 1) = \frac{1}{x^{3}} - 1$
$(\frac{1}{x} - 1) (\frac{1}{x^{3}} + \frac{1}{x^{2}} + \frac{1}{x} + 1) = \frac{1}{x^{4}} - 1 \cdot \cdot \cdot \cdot \cdot \cdot$

(1)、从上面的算式及计算结果，根据你发现的规律直接写下面的空格： $(\frac{1}{x} - 1) (\frac{1}{x^{7}} + \frac{1}{x^{6}} + \frac{1}{x^{5}} + \frac{1}{x^{4}} + \frac{1}{x^{3}} + \frac{1}{x^{2}} + \frac{1}{x} + 1) =$ ；

(2)、用数学的整体思想方法，设 $\frac{1}{x} = m$ ，分解因式： $(m^{7} + m^{6} + m^{5} + m^{4} + m^{3} + m^{2} + m + 1)$ ， $(m \neq 1)$ ；

(3)、已知 $1 + 2 + 2^{2} + 2^{3} + 2^{4} + 2^{5} + 2^{6} + 2^{7} = a \cdot b \cdot c \cdot d$ ， a、b、c、d都是正整数，且 $a > b > c > d$ ，化简求 ${(- \frac{b}{c d})}^{2} \div (- \frac{5 b}{17 c}) \times \frac{6 d}{a}$ 的值.

查看试题解析
25. 如图， $A$ 种小麦试验田是边长为 $a$ 的正方形中减去一个边长为 $b$ 的正方形蓄水池后余下的部分； $B$ 种小麦试验田是边长为 $\frac{1}{2} (a + b)$ 的正方形.

(1)、设两块试验田都收获了 $m (kg)$ 小麦，求 $A$ ， $B$ 两种小麦单位面积产量的比.

(2)、当 $a = 2 b$ 时， $A$ ， $B$ 两种小麦单位面积产量哪个较大？

(3)、若 $A$ ， $B$ 两种小麦单位面积产量相同，求 $a$ ， $b$ 满足的关系式.

查看试题解析
26. 我们规定：分式中，在分子、分母都是整式的情况下，如果分子的次数低于分母的次数，称这样的分式为真分式．例如，分式 $\frac{4}{x + 2}$ ， $\frac{3 x^{2}}{x^{3} － 4 x}$ 是真分式．如果分子的次数不低于分母的次数，称这样的分式为假分式．例如，分式 $\frac{x + 1}{x － 1}$ ， $\frac{x^{2}}{x + 1}$ 是假分式．一个假分式可以化为一个整式与一个真分式的和．例如， $\frac{x + 1}{x － 1}$ = $\frac{(x - 1) + 2}{x － 1}$ =1＋ $\frac{2}{x － 1}$ ， $\frac{2 x - 3}{x + 1}$ = $\frac{2 x + 2 - 5}{x + 1}$ = $\frac{2 x + 2}{x + 1}$ + $\frac{- 5}{x + 1}$ = 2＋ $\frac{- 5}{x + 1}$ ．

(1)、将假分式 $\frac{4 x － 5}{x + 1}$ 化为一个整式与一个真分式的和；

(2)、将假分式 $\frac{a^{2} － 4 a + 6}{a － 1}$ 化成一个整式与一个真分式的和的形式为： $\frac{a^{2} － 4 a + 6}{a － 1}$ = a＋m＋ $\frac{n}{a － 1}$ ，求m、n的值；并直接写出当整数a为何值时，分式 $\frac{a^{2} － 4 a + 6}{a － 1}$ 为正整数；

(3)、自然数A是 $\frac{10^{18} + 2022}{10^{9} + 2}$ 的整数部分，则A的数字和为．（把组成一个数的各个数位上的数字相加，所得的和，就叫做这个数的数字和．例如：126的数字和就是1+2+6=9）

查看试题解析