2022-2023学年人教版八年级数学下期末复习 一次函数
试卷更新日期:2023-05-12 类型:复习试卷
一、单选题
-
1. 下面哪个点不在函数y=-2x+3的图象上( )A、 B、 C、 D、2. 函数① ;② ;③ ;④ 中, 是 的一次函数的有( )A、1个 B、2个 C、3个 D、4个3. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、
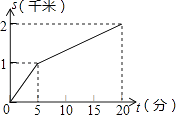 B、
B、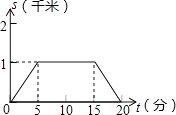 C、
C、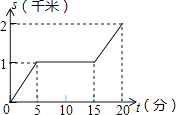 D、
D、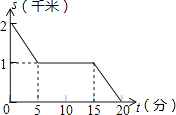 4. 如图,已知正比例函数与一次函数的图象交于点P.下面有四个结论:①;②;③当时,;④当时,.其中正确的是( )
4. 如图,已知正比例函数与一次函数的图象交于点P.下面有四个结论:①;②;③当时,;④当时,.其中正确的是( )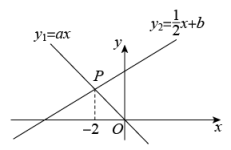 A、①② B、②③ C、①③ D、①④5. 已知直线 与直线 平行,且直线l经过第二,三、四象限,则b的取值范围为( )A、 B、 C、 D、6. 若直线 经过点 ,直线 经过点 ,且 与 关于 轴对称,则 与 的交点坐标为( )A、 B、 C、 D、7. 正方形的周长y是边长x的函数,则下列表示正方形周长y与边长x之间的函数关系正确的是( )A、 B、 C、y=x2(x>0) D、8. 将一次函数y =2x-3的图象沿y轴向上平移3个单位长度后,所得图象的函数表达式为( )A、y=2x B、y=2x-6 C、y=5x-3 D、y= -x-39. 已知,△ABC中,∠BAC=135°,AB=AC=2 ,P为边AC上一动点,PQ∥BC交AB于Q,设PC=x, △PCQ的面积为y,则y与x的函数关系图象是( )A、
A、①② B、②③ C、①③ D、①④5. 已知直线 与直线 平行,且直线l经过第二,三、四象限,则b的取值范围为( )A、 B、 C、 D、6. 若直线 经过点 ,直线 经过点 ,且 与 关于 轴对称,则 与 的交点坐标为( )A、 B、 C、 D、7. 正方形的周长y是边长x的函数,则下列表示正方形周长y与边长x之间的函数关系正确的是( )A、 B、 C、y=x2(x>0) D、8. 将一次函数y =2x-3的图象沿y轴向上平移3个单位长度后,所得图象的函数表达式为( )A、y=2x B、y=2x-6 C、y=5x-3 D、y= -x-39. 已知,△ABC中,∠BAC=135°,AB=AC=2 ,P为边AC上一动点,PQ∥BC交AB于Q,设PC=x, △PCQ的面积为y,则y与x的函数关系图象是( )A、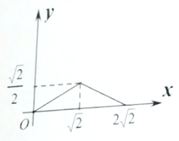 B、
B、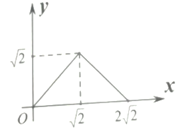 C、
C、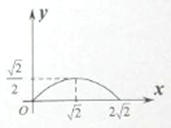 D、
D、 10. 如图,是某工程队修路的长度y(单位:m)与修路时间t(单位:天)之间的函数关系.该工程队承担了一项修路任务,任务进行一段时间后,工程队提高了工作效率,则该工程队提高效率前每天修路的长度是( ) 米.
10. 如图,是某工程队修路的长度y(单位:m)与修路时间t(单位:天)之间的函数关系.该工程队承担了一项修路任务,任务进行一段时间后,工程队提高了工作效率,则该工程队提高效率前每天修路的长度是( ) 米.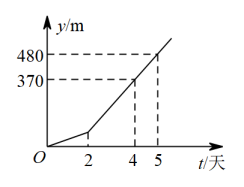 A、150 B、110 C、75 D、70
A、150 B、110 C、75 D、70二、填空题
-
11. 一次函数 的图象与y轴的交点坐标是 .12. 过点(-1,7)的一条直线与x轴,y轴分别相交于点A,B,且与直线y=- x+1平行.则在线段AB上,横、纵坐标都是整数的点的坐标是 .
13. 一次函数y=﹣x+b图象经过点(2,﹣4),则b= .14. 当m=时,函数y=-(m-2) +(m-4)是关于x的一次函数.15. 在平面直角坐标系中,以O,A,B,C为顶点的平行四边形的顶点O(0,0),A(6,0),B(2,2),C(m,n),直线y=kx+2平分该平行四边形的周长,则k的值为 .三、解答题
-
16. 已知y﹣2与2x+3成正比例,当x=1时,y=12,求y与x的函数关系式.17. 已知一次函数 ,当 时y的值是 ,当 时y的值是 .求此一次函数的解析式.18. 直线y=﹣ x+4与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
①请直接写出点C、点D的坐标,并求出m的值;
②点P(0,t)是线段OB上的一个动点(点P不与0、B重合),
经过点P且平行于x轴的直线交AB于M、交CE于N.设线段MN的长度为d,求d与t之间的函数关系式(不要求写自变量的取值范围);
③当t=2时,线段MN,BC,AE之间有什么关系?(写出过程)
 19. 如图,直线 : 与直线 : 相交于点P(1,b)
19. 如图,直线 : 与直线 : 相交于点P(1,b)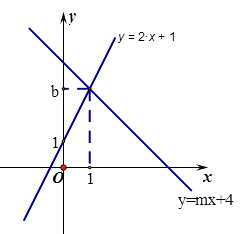 (1)、求b,m的值(2)、垂直于x轴的直线 与直线 , 分别相交于C,D,若线段CD长为2,求a的值20. 甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:
(1)、求b,m的值(2)、垂直于x轴的直线 与直线 , 分别相交于C,D,若线段CD长为2,求a的值20. 甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题: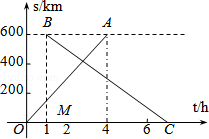 (1)、从图象看,普通快车发车时间比第一列动车组列车发车时间1h(填”早”或”晚”),点B的纵坐标600的实际意义是;(2)、请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象;(3)、若普通快车的速度为100km/h,
(1)、从图象看,普通快车发车时间比第一列动车组列车发车时间1h(填”早”或”晚”),点B的纵坐标600的实际意义是;(2)、请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象;(3)、若普通快车的速度为100km/h,①求第二列动车组列车出发多长时间后与普通快车相遇?
②请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.
21.在烧开水时,水温达到100℃就会沸腾,下表是某同学做“观察水的沸腾”实验时记录的数据:

(1)上表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间推移2分钟,水的温度如何变化?
(4)时间为8分钟,水的温度为多少?你能得出时间为9分钟时,水的温度吗?
(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?
(6)为了节约能源,你认为应在什么时间停止烧水?
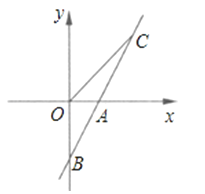
22. 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
 23. 如图1,长为60km的某段线路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B、A后立刻返回到出发站停止,速度均为30km/h,设甲车,乙车距南站A的路程分别为y甲 , y乙(km)行驶时间为t(h).
23. 如图1,长为60km的某段线路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B、A后立刻返回到出发站停止,速度均为30km/h,设甲车,乙车距南站A的路程分别为y甲 , y乙(km)行驶时间为t(h).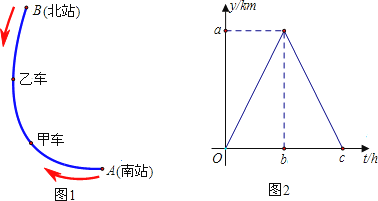
(1)图2已画出y甲与t的函数图象,其中a= , b= , c= .
(2)分别写出0≤t≤2及2<t≤4时,y乙与时间t之间的函数关系式.
(3)在图2中补画y乙与t之间的函数图象,并观察图象得出在整个行驶过程中两车相遇的次数.