人教版2022-2023学年度第二学期八年级数学二次根式期末复习

试卷更新日期：2023-05-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列各式中正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt{x^{2}} = x$ C、 $\sqrt[3]{(- x)^{3}} = - x$ D、 $\sqrt{(- x)^{2}} = - x$

查看试题解析
2. 要使代数式 $\sqrt{4 - 3 x}$ 有意义，则下列数值中字母 $x$ 不能取的是（）

A、-2 B、0 C、1 D、2

查看试题解析
3. 若 $\sqrt{(a - b)^{2}}$ ＝-a-b，则（）

A、|a+b|＝0 B、|a-b|＝0 C、|ab|＝0 D、|a²+b²|＝0

查看试题解析
4. 下列x的值使二次根式 $\sqrt{2 - x}$ 无意义的是．（）

A、x=-5 B、x=0 C、x= 2 D、x=3

查看试题解析
5. 要使二次根式 $\sqrt{x + 1}$ 有意义，则x应满足（）

A、x>1 B、x<-1 C、x<1 D、x≥-1

查看试题解析
6. 要使代数式 $\frac{x}{\sqrt{x + 1}}$ 有意义，则 $x$ 的取值范围是（）

A、 $x > - 1$ B、 $x \geq - 1$ C、 $x \neq 0$ D、 $x > - 1$ 且 $x \neq 0$

查看试题解析
7. 如图，矩形内有两个相邻的白色正方形，其面积分别为2和18，则图中阴影部分的面积为（）

A、 $2 \sqrt{2}$ B、 $4 \sqrt{2}$ C、4 D、6

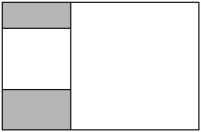查看试题解析
8. 已知m、n是两个连续自然数（m＜n），且 $q = m n$ ， $p = \sqrt{q + n} + \sqrt{q - m}$ ，则p（）

A、总是奇数 B、总是偶数 C、有时奇数，有时偶数 D、有时是有理数，有时是无理数

查看试题解析
9. 已知 $- 1 < a < 0$ ，化简 $\sqrt{(a + \frac{1}{a})^{2} - 4} - \sqrt{(a - \frac{1}{a})^{2} + 4}$ 的结果为（）

A、 $2 a$ B、 $- 2 a$ C、 $- \frac{2}{a}$ D、 $\frac{2}{a}$

查看试题解析
10. 化简 $\sqrt{\frac{1}{2}}$ 的结果是（）

A、1 B、 $\sqrt{2}$ C、2 D、 $\frac{\sqrt{2}}{2}$

查看试题解析

二、填空题

11. 若 $\sqrt{x - 3}$ 在实数范围内有意义，则x满足 .

查看试题解析
12. 当x=时， $\sqrt{2 x - 6}$ 的值最小．

查看试题解析
13. 化简二次根式 $\sqrt{\frac{4}{5}}$ 的结果为 .

查看试题解析
14. 已知 $\sqrt{m - 2}$ （m-3）≤0.若整数a满足m+a＝5 $\sqrt{2}$ ，则a＝.

查看试题解析
15. 若式子 $\frac{\sqrt{x + 3}}{x - 2}$ 有意义，则x的取值范围是

查看试题解析

三、解答题

16. 已知 $| x - 3 | + \sqrt{x - y + 1} = 0$ ，求 $\sqrt{x^{2} y + x y^{2} + \frac{1}{4} y^{3}}$ 的值．

查看试题解析
17. 若有理数x、y、z满足 $\sqrt{x} + \sqrt{y - 1} + \sqrt{z - 2} = \frac{1}{2} (x + y + z)$ ，求 ${(x - y z)}^{3}$ 的值.

查看试题解析
18. 若x，y为实数，且y＝ $\sqrt{x - 3}$ + $\sqrt{3 - x}$ +x+5，化简： $\sqrt{\frac{y}{x}}$ ．

查看试题解析

四、综合题

19. $\sqrt{a^{2}} = | a |$ 是二次根式的一条重要性质，请利用该性质解答以下问题：

(1)、化简： $\sqrt{(- 3)^{2}} =$ ， $\sqrt{(3 - π)^{2}} =$ ；

(2)、已知实数 $a$ ， $b$ ， $c$ 在数轴上的对应点如图所示，化简 $- | c - a | + \sqrt{(b - c)^{2}}$ ．

查看试题解析
20. 如图，平面直角坐标系中，把矩形 $O A B C$ 沿对角线 $O B$ 所在的直线折叠，点 $A$ 落在点 $D$ 处， $O D$ 与 $B C$ 交于点 $E$ ． $O A$ ， $O C$ 的长满足式子 $| O A - 6 | + \sqrt{O C^{2} - 9} = 0$ ．

(1)、求点 $A$ ， $C$ 的坐标；

(2)、直接写出点 $E$ 的坐标，并求出直线 $A E$ 的函数解析式；

(3)、 $F$ 是 $x$ 轴上一点，在坐标平面内是否存在点 $P$ ，使以 $O$ ， $B$ ， $P$ ， $F$ 为顶点的四边形为菱形？若存在，请直接写出点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析
21. 阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如： $3 + 2 \sqrt{2} = (1 + \sqrt{2})^{2}$ ，善于思考的小明进行了以下探索：
设 $a + b \sqrt{2} = (m + n \sqrt{2})^{2}$ （其中 $a ， b ， m ， n$ 均为整数），则有 $a + b \sqrt{2} = m^{2} + 2 n^{2} + 2 m n \sqrt{2}$ . $∴ a = m^{2} + 2 n^{2} ， b = 2 m n$ .这样小明就找到了一种把部分 $a + b \sqrt{2}$ 的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题：

(1)、当 $a ， b ， m ， n$ 均为正整数时，若 $a + b \sqrt{3} = (m + n \sqrt{3})^{2}$ ，用含 $m ， n$ 的式子分别表示 $a ， b$ ，得 $a =$ ， $b =$ ；

(2)、若 $a + 4 \sqrt{3} = (m + n \sqrt{3})^{2}$ ，且 $a ， m ， n$ 均为正整数，求 $a$ 的值.

查看试题解析
22. 在学习了算术平方根和二次根式等内容后，我们知道以下的结论：
结论①：若实数 $a \geq 0$ 时， ${(\sqrt{a})}^{2} = a$ ；结论②：对于任意实数a， $\sqrt{a^{2}} = | a |$ ．
请根据上面的结论，对下列问题进行探索：

(1)、若 $m < 2$ ，化简： $\sqrt{{(m - 2)}^{2}} + | m - 3 |$ ．

(2)、若 $\sqrt{a^{2}} = 4$ ， $| b | = 8$ ，且 $a b > 0$ ，求 $a + b$ 的值．

(3)、若 $A = {(\sqrt{m - 2})}^{2} + | 1 - m |$ 有意义，化简 $A$ ．

查看试题解析
23. 阅读下列解题过程：
例：若代数式 $\sqrt{(2 - a)^{2}} + \sqrt{(a - 4)^{2}} = 2$ ，求a的取值．
解：原式 $= | a - 2 | + | a - 4 |$ ，
当 $a < 2$ 时，原式 $= (2 - a) + (4 - a) = 6 - 2 a = 2$ ，解得 $a = 2$ （舍去）；
当 $2 \leq a < 4$ 时，原式 $= (a - 2) + (4 - a) = 2$ ，等式恒成立；
当 $a \geq 4$ 时，原式 $= (a - 2) + (a - 4) = 2 a - 6 = 2$ ，解得 $a = 4$ ；
所以，a的取值范围是 $2 \leq a \leq 4$ ．
上述解题过程主要运用了分类讨论的方法，请你根据上述理解，解答下列问题：

(1)、当 $3 \leq a \leq 7$ 时，化简： $\sqrt{(3 - a)^{2}} + \sqrt{(a - 7)^{2}}$ ；

(2)、若 $\sqrt{(a + 1)^{2}} + \sqrt{(a - 3)^{2}} = 6$ ，求a的取值；

(3)、请直接写出满足 $\sqrt{(a - 1)^{2}} + \sqrt{(a - 6)^{2}} = 5$ 的a的取值范围．

查看试题解析

人教版2022-2023学年度第二学期八年级数学 二次根式 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

人教版2022-2023学年度第二学期八年级数学二次根式期末复习