浙江省杭州地区(含周边)重点中学2022-2023学年高一下学期数学期中试卷
试卷更新日期:2023-05-12 类型:期中考试
一、单选题
-
1. 已知 , 且 , 则等于( )A、-2 B、2 C、 D、2. 设复数(为虚数单位),则的模等于( )A、 B、5 C、 D、103. 已知中, , 则等于( )A、 B、 C、 D、4. 直径为的一个大金属球,熔化后铸成若干个直径为的小球,如果不计损耗,可铸成这样的小球的个数为( )A、3 B、6 C、9 D、275. 如图,梯形是一水平放置的平面图形在斜二测画法下的直观图.若平行于轴, , 则平面图形的面积是( )
 A、14 B、7 C、 D、6. 设a=log37,b=21.1 , c=0.83.1 , 则( )A、b<a<c B、a<c<b C、c<b<a D、c<a<b7. 如图,正方体的棱长为为的中点,为的中点,过点的平面截正方体所得的截面的面积( )
A、14 B、7 C、 D、6. 设a=log37,b=21.1 , c=0.83.1 , 则( )A、b<a<c B、a<c<b C、c<b<a D、c<a<b7. 如图,正方体的棱长为为的中点,为的中点,过点的平面截正方体所得的截面的面积( ) A、 B、 C、 D、8. 已知非零向量 , 满足 , , 且 , 则的最小值为( )A、 B、3 C、 D、1
A、 B、 C、 D、8. 已知非零向量 , 满足 , , 且 , 则的最小值为( )A、 B、3 C、 D、1二、多选题
-
9. 下列说法中,正确的有( )A、复数满足; B、“为钝角”是“复数在复平面内对应的点在第二象限”的充要条件; C、已知复数“的虚部相等”是“”的必要条件 D、在复数范围内,若是关于的实系数方程的一根,则该方程的另一根是10. 已知的内角所对的边分别为 , 下列四个命题中正确的是( )A、若 , 则一定是钝角三角形 B、若 , 则一定是锐角三角形 C、若 , 则一定是等腰三角形 D、若 , 则一定是等边三角形11. 已知三棱锥中, , 分别是的中点,是棱上(除端点外)的动点,下列选项正确的是( )
 A、直线与是异面直线; B、当时,三棱锥体积为; C、的最小值为; D、三棱锥外接球的表面积.12. 已知函数满足:则下列判断正确的是( )A、为奇函数 B、是周期函数且最小正周期为6 C、 D、的图象关于直线对称
A、直线与是异面直线; B、当时,三棱锥体积为; C、的最小值为; D、三棱锥外接球的表面积.12. 已知函数满足:则下列判断正确的是( )A、为奇函数 B、是周期函数且最小正周期为6 C、 D、的图象关于直线对称三、填空题
-
13. 若向量 , 则在上的投影向量坐标为.14. 已知集合 , 若“”是“”的必要不充分条件,则实数的取值范围为.15. 在中,点在边上, , 若边上的高与边上的高之比为 , 则.16. 已知则的最大值为.
四、解答题
-
17. 已知复数满足.(1)、求;(2)、求.18. 正三棱台中,.
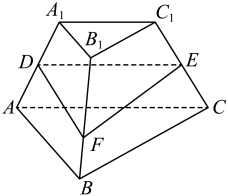 (1)、求三棱台的表面积;(2)、分别是的中点,为上一点,且 , 几何体的体积记为 , 几何体的体积记为 , 求的值.19. 如图所示,有两个兴趣小组同时测量一个小区内的假山高度,已知该小区每层楼高4.
(1)、求三棱台的表面积;(2)、分别是的中点,为上一点,且 , 几何体的体积记为 , 几何体的体积记为 , 求的值.19. 如图所示,有两个兴趣小组同时测量一个小区内的假山高度,已知该小区每层楼高4.
附:.
(1)、兴趣小组1借助测角仪进行测量,在假山水平面C点测得B点的仰角为15°,在六楼A点处测得B点的俯角为45°,求假山的高度(精确到0.1);(2)、兴趣小组2借助测距仪进行测量,可测得AB=22 , BC=16 , 求假山的高度(精确到0.1).
