四川省成都市蓉城高中联盟2022-2023学年高二下学期理数期中考试试卷

试卷更新日期：2023-05-12 类型：期中考试

进入出卷网下载

一、单选题

1. 在空间直角坐标系 $O - x y z$ 中，点 $A (1 ， 2 ， 3)$ 关于x轴对称的点的坐标为（）

A、 $(- 1 ， - 2 ， - 3)$ B、 $(- 1 ， 2 ， - 3)$ C、 $(1 ， - 2 ， - 3)$ D、 $(- 1 ， - 2 ， 3)$

查看试题解析
2. 下列导数运算正确的是（）

A、 ${(c o s x)}^{^{'}} = s i n x$ B、 ${(2^{x})}^{^{'}} = 2^{x}$ C、 ${(l o g_{3} x)}^{^{'}} = \frac{1}{x l n 3}$ D、 ${(\frac{1}{x})}^{^{'}} = \frac{1}{x^{2}}$

查看试题解析
3. $\vec{a} = (- 1 ， 2 ， - 3)$ ， $\vec{b} = (2 ， x ， 6)$ ，若 $\vec{a}$ // $\vec{b}$ ，则 $x =$ （）

A、0 B、-4 C、4 D、2

查看试题解析
4. 已知函数 $y = f (x) (x \in R)$ 的导函数 $f^{'} (x)$ 的图像如图所示，则函数 $y = f (x)$ （）

A、在 $(- \infty ， - 2)$ 上单调递增 B、在 $(1 ， + \infty)$ 上单调递减 C、在 $(- \infty ， 3)$ 上单调递增 D、在 $(3 ， + \infty)$ 上单调递减

查看试题解析
5. 已知 $A (2 ， 0 ， 0)$ ， $B (0 ， 2 ， 0)$ ， $C (0 ， 0 ， 2)$ ，则平面ABC的一个法向量可以是（）

A、 $(- 1 ， - 1 ， - 1)$ B、 $(1 ， - 1 ， 1)$ C、 $(- 1 ， 1 ， 1)$ D、 $(1 ， 1 ， - 1)$

查看试题解析
6. 若直线l的方向向量与平面 $α$ 的法向量的夹角等于 $\frac{2 π}{3}$ ，则直线l与平面 $α$ 所成的角等于（）

A、 $\frac{2 π}{3}$ B、 $\frac{π}{3}$ C、 $\frac{π}{6}$ D、 $\frac{π}{4}$

查看试题解析
7. 已知 $f (x) = x l n x$ ，则曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程为（）

A、 $x - y - 1 = 0$ B、 $x - y - 2 = 0$ C、 $x + y - 1 = 0$ D、 $x + y - 2 = 0$

查看试题解析
8. 已知 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 均为空间单位向量，它们之间的夹角均为 $9 0^{∘}$ ，那么 $| \vec{a} - 2 \vec{b} + 3 \vec{c} | =$ （）

A、2 B、 $\sqrt{13}$ C、 $\sqrt{14}$ D、6

查看试题解析
9. 已知函数 $f (x) = l n x + x^{2} + b x$ 的单调递减区间为 $(\frac{1}{2} ， 1)$ ，则 $b$ 的值为（）

A、3 B、-6 C、6 D、-3

查看试题解析
10. 如图，将 $∠ A = 6 0^{∘}$ 的菱形ABCD沿对角线BD折起，使得平面 $A B D ⊥$ 平面CBD，则异面直线AB与CD所成角的余弦值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $- \frac{1}{2}$ D、 $- \frac{1}{4}$

查看试题解析
11. 若函数 $f (x) = x^{2} + a x + l n x$ 有两个不同的极值点，则实数a的取值范围为（）

A、 $a < - 2 \sqrt{2}$ B、 $a > 2 \sqrt{2}$ C、 $- 2 \sqrt{2} < a < 2 \sqrt{2}$ D、 $a < - 2 \sqrt{2}$ 或 $a > 2 \sqrt{2}$

查看试题解析
12. 已知 $a = 0.98 - l n 0.98$ ， $b = 1$ ， $c = 1.02 - 1.02 l n 1.02$ ，则（）

A、 $a < b < c$ B、 $c < b < a$ C、 $b < c < a$ D、 $b < a < c$

查看试题解析

二、填空题

13. $\int \begin{matrix} \frac{π}{2} \\ 0 \end{matrix} cos x d x =$ ．

查看试题解析
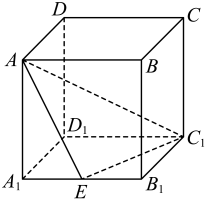
14. 已知直线l在平面 $α$ 外，直线l的方向向量是 $\vec{a} = (1 ， 2 ， 3)$ ，平面 $α$ 的法向量是 $\vec{m} = (1 ， - 2 ， 1)$ ，则l与 $α$ 的位置关系是（填“平行”或“相交”）

查看试题解析
15. 如图，在棱长为1的正方体 $B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E为线段 $A_{1} B_{1}$ 的中点，则点C到平面 $A E C_{1}$ 的距离等于.

查看试题解析
16. 已知不等式 $k (x + 2) e^{x} < x + 1$ 恰有2个整数解，则实数k的取值范围为.

查看试题解析

三、解答题

17. 如图，在平行六面体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E，F分别为棱 $A_{1} D_{1}$ ， CD的中点，记 $\vec{B C} = \vec{a}$ ， $\vec{B A} = \vec{b}$ ， $\vec{B B_{1}} = \vec{c}$ ，满足 $∠ B_{1} B C = ∠ B_{1} B A = \frac{π}{3}$ ， $∠ C B A = \frac{π}{2}$ ， $| A B | = | B C | = 2$ ， $| B B_{1} | = 3$ .

(1)、用 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 表示 $\vec{F E}$ ；

(2)、计算 $\vec{B C} \cdot \vec{F E}$ .

查看试题解析
18. 已知函数 $f (x) = \frac{1}{3} x^{3} - a x^{2} + 3$ 在点 $(1 ， f (1))$ 处的切线与直线 $x - y + 3 = 0$ 垂直.

(1)、求a的值

(2)、求函数 $f (x)$ 的极值.

查看试题解析
19. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 2$ ， $A D = 4$ ， $A A_{1} = 3$ ， $B_{1} C$ 交 $B C_{1}$ 于点E.

(1)、证明：直线 $D_{1} E / /$ 平面 $A_{1} B D$ ；

(2)、求AD与平面 $A_{1} B D$ 所成角的正弦值.

查看试题解析
20. 一艘渔船在进行渔业作业的过程中，产生的主要费用有燃油费用和人工费用，已知渔船每小时的燃油费用与渔船速度的立方成正比，已知当渔船的速度为10海里/小时时，燃油费用是600元/小时，人工费用是4050元/小时，记渔船的航行速度为v（海里/小时），满足 $0 ≤ v ≤ 30$ ，渔船每航行1海里产生的主要费用为p元

(1)、列出航行1海里产生的主要费用p（元）关于航行速度v（海里/小时）的关系式；

(2)、求航行1海里产生的主要费用p（元）的最小值，及此时渔船的航行速度v（海里小时）的大小.

查看试题解析
21. 如图，四边形ABCD为等腰梯形（如图①）， $B E ⊥ A D$ ， $C F ⊥ A D$ ，点E，F为垂足，满足 $A E = B E = B C = 2$ ，将 $△ A B E$ 和 $△ D C F$ 分别沿BE，CF折起，使A，D两点重合于点P（如图②）

(1)、证明：平面 $P E F ⊥$ 平面BCFE；

(2)、求二面角 $P - B C - E$ 的余弦值.

查看试题解析
22. 已知函数 $f (x) = x - (a + 1) l n x - \frac{a}{x}$ .

(1)、讨论函数 $f (x)$ 的单调性：

(2)、若 $x_{1}$ ， $x_{2}$ 是函数 $f (x)$ 的两个不同极值点，且满足： $x_{1} < x_{2}$ ， $x_{2} > 1$ ，求证： $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 1 + 3 a$ .

查看试题解析