陕西省宝鸡市千阳县2022-2023学年高二下学期理数期中试卷

试卷更新日期：2023-05-12 类型：期中考试

进入出卷网下载

一、单选题

1. 已知复数 $z_{1} = 2 + i$ ， $z_{2} = 1 + i$ ，则 $\frac{z_{1}}{z_{2}}$ 在复平面内对应的点位于（　　）

A、第一象限 B、第三象限 C、第二象限 D、第四象限

查看试题解析
2. 安排4名大学生去3所学校支教，每人只能去一个学校，每个学校至少分配一名大学生，则不同的分派方法共有（）

A、36种 B、24种 C、18种 D、12种

查看试题解析
3. 若复数 $\frac{a + i}{1 - i}$ 为纯虚数，则它的共轭复数是（）

A、 $2 i$ B、 $- 2 i$ C、 $i$ D、 $- i$

查看试题解析
4. $\int_{0}^{2 π}$ |sinx|dx等于（）

A、0 B、1 C、2 D、4

查看试题解析
5. 已知 $x_{1} > 0 ， x_{1} \neq 1$ ，且 $x_{n + 1} = \frac{x_{n} (x_{n}^{2} + 3)}{3 x_{n}^{2} + 1} (n \in N_{+})$ ，试证"数列 ${x_{n}}$ 对任意正整数 $n$ 都满足 $x_{n} < x_{n + 1}$ ，或者对任意正整数 $n$ 都满足 $x_{n} > x_{n + 1}$ ，当此题用反证法否定结论时，应为（）

A、对任意的正整数 $n$ ，都有 $x_{n} = x_{n + 1}$ B、存在正整数 $n$ ，使 $x_{n} > x_{n + 1}$ C、存在正整数 $n (n \geq 2)$ ，使 $x_{n} \geq x_{n + 1}$ 且 $x_{n} \leq x_{n - 1}$ D、存在正整数 $n (n \geq 2)$ ，使 $(x_{n} - x_{n - 1}) (x_{n} - x_{n + 1}) \geq 0$

查看试题解析
6. 设 $m = \int_{0}^{1} e^{x} d x$ ， $n = \int_{1}^{e} \frac{1}{x} d x$ ，则 $m$ 与 $n$ 的大小关系为（）

A、 $m < n$ B、 $m \leq n$ C、 $m > n$ D、 $m \geq n$

查看试题解析
7. 函数 $y = {(s i n x^{2})}^{3}$ 的导数是（）

A、 $y = 3 x s i n x^{2} \cdot s i n 2 x^{2}$ B、 $y = 3 {(s i n x^{2})}^{2}$ C、 $y = 3 {(s i n x^{2})}^{2} c o s x^{2}$ D、 $y = 6 s i n x^{2} c o s x^{2}$

查看试题解析
8. 在 $(x - \sqrt{2})^{6}$ 的展开式中， $x^{3}$ 的系数为（）

A、 $- 40 \sqrt{2}$ B、 $40 \sqrt{2}$ C、-40 D、40

查看试题解析
9.
函数f(x)的定义域为开区间(a ， b)，导函数f′(x)在(a ， b)内的图象如图所示，则函数f(x)在开区间(a ， b)内有极小值点(　　)

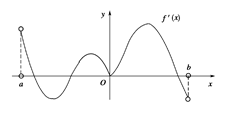A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 已知函数 $f (x)$ 在R上可导，且 $f (x) = x^{2} f^{'} (2) - 3 x$ ，则 $f (- 1)$ 与 $f (1)$ 的大小关系是

A、 $f (- 1) = f (1)$ B、 $f (- 1) > f (1)$ C、 $f (- 1) < f (1)$ D、不确定

查看试题解析
11. 若不等式2xln x≥－x²＋ax－3对x∈(0，＋∞)恒成立，则实数a的取值范围是(　　)

A、(－∞，0) B、(－∞，4] C、(0，＋∞) D、[4，＋∞)

查看试题解析
12. 已知定义在R上的函数 $f (x)$ 满足 $f^{'} (x) > f (x)$ .若 $x_{1} < x_{2}$ ，则（）

A、 $e^{x_{1}} f (x_{2}) > e^{x_{2}} f (x_{1})$ B、 $e^{x_{1}} f (x_{2}) < e^{x_{2}} f (x_{1})$ C、 $e^{x_{1}} f (x_{2}) = e^{x_{2}} f (x_{1})$ D、 $e^{x_{1}} f (x_{2})$ 与 $e^{x_{2}} f (x_{1})$ 的大小关系不确定

查看试题解析

二、填空题

13. 复数 $z$ 满足 $(1 + i) z = | \sqrt{3} - i |$ ，则 $z$ 的共轭复数 $\bar{z} =$ .

查看试题解析
14. 已知函数f（x）=a^xlnx，x∈（0，+∞），其中a为实数，f′（x）为f（x）的导函数，若f′（1）=3，则a的值为

查看试题解析
15. 某商场从生产厂家以每件20元购进一批商品，若该商品零售价为p元，销量Q(单位：件)与零售价p(单位：元)有如下关系：Q＝8 300－170p－p² ，则该商品零售价定为元时利润最大，利润的最大值为元．

查看试题解析
16. 两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数，按照点或小石子能排列的形状对数进行分类.下图中实心点的个数5，9，14，20， $⋯$ ，被称为梯形数.根据图形的构成，记第2018个梯形数为 $a_{2018}$ ，则 $a_{2018} =$ .

查看试题解析

三、解答题

17. 某中学将要举行校园歌手大赛，现有4男3女参加，需要安排他们的出场顺序．（结果用数字作答）

(1)、如果3个女生都不相邻，那么有多少种不同的出场顺序？

(2)、如果3位女生都相邻，且男生甲不在第一个出场，那么有多少种不同的出场顺序？

查看试题解析
18. 已知二项式 ${(a x + \frac{1}{\sqrt{x}})}^{n}$ 的第三项和第八项的二项式系数相等.

(1)、求 $n$ 的值；

(2)、若展开式的常数项为 $84$ ，求 $a$ .

查看试题解析
19. 已知复数 $z = \frac{(1 - i)^{2} + 3 (1 + i)}{2 - i}$ ．

(1)、若复数 $z_{1}$ 与 $z$ 在复平面上所对应的点关于虚轴对称，求 $z_{1}$ ；

(2)、若实数a，b满足 $z^{2} + a z + b = 1 - i$ ，求 $z_{2} = a + b i$ 的共轭复数．

查看试题解析
20. 已知函数 $f (x) = e^{x + 2} (x^{2} - 3)$ ．

(1)、求曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；

(2)、求函数 $y = f (x)$ 的极值．

查看试题解析
21. 如图，在三棱锥 $P - A B C$ 中， $A B ⊥ B C ， A B = B C = 2 ， P A = P B = P C = 2 \sqrt{2} ， O$ 为 $A C$ 的中点.

(1)、证明： $A C ⊥$ 平面 $P B O$ ；

(2)、若 $M$ 为棱 $B C$ 的中点，求二面角 $M - P A - C$ 的正弦值.

查看试题解析
22. 已知函数 $f (x) = 2 x^{3} - a x^{2} + b$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、是否存在 $a ， b$ ，使得 $f (x)$ 在区间 $[0 ， 1]$ 的最小值为 $- 1$ 且最大值为1？若存在，求出 $a ， b$ 的所有值；若不存在，说明理由.

查看试题解析