安徽省庐巢七校联考2022-2023学年高二下学期3月期中数学试题

试卷更新日期：2023-05-12 类型：期中考试

进入出卷网下载

一、单选题

1. 设函数 $f (x)$ 在 $x = 1$ 处的导数为2，则 $\underset{Δ x \to 0}{l i m} \frac{f (1 + 3 Δ x) - f (1)}{Δ x} =$ （）

A、-2 B、2 C、 $\frac{2}{3}$ D、6

查看试题解析
2. 某小组有8名男生，6名女生，要求从中选1名当组长，不同的选法共有（）

A、12种 B、14种 C、24种 D、48种

查看试题解析
3. 已知某物体在平面上做变速直线运动，且位移 $s$ （单位：米）与时间 $t$ （单位：秒）之间的关系可用函数： $s = l n (t + 1) + t^{2} - t$ 表示，则该物体在 $t = 3$ 秒时的瞬时速度为（）

A、 $\frac{21}{4}$ 米/秒 B、 $(6 + 2 l n 2)$ 米/秒 C、 $\frac{21}{2}$ 米/秒 D、 $(4 + l n 2)$ 米秒

查看试题解析
4. 函数 $f (x) = 2 x - 5 l n x - 4$ 的单调递增区间是（）

A、 $(\frac{5}{2} ， + \infty)$ B、 $(- ∞ ， 0)$ 和 $(\frac{5}{2} ， + \infty)$ C、 $(0 ， \frac{5}{2})$ D、 $(0 ， 3)$

查看试题解析
5. 设函数 $h (x) = \frac{f (x) + 5}{g (x)}$ ，已知 $f (2) = 5$ ， $f^{'} (2) = 3$ ， $g (2) = 2$ ， $g^{'} (2) = 1$ ，则 $h^{'} (2) =$ （）

A、－2 B、－1 C、 $\frac{1}{4}$ D、3

查看试题解析
6. 已知 $R$ 上的函数 $f (x)$ 满足 $f (1) = 3$ ，且 $f^{'} (x) < 2$ ，则不等式 $f (x) < 2 x + 1$ 的解集为（）

A、 $(- \infty ， 1)$ B、 $(3 ， + \infty)$ C、 $(1 ， + \infty)$ D、 $(2 ， + \infty)$

查看试题解析
7. 若 $y = a x + b$ 是 $f (x) = x \ln x$ 的切线，则 $\frac{a}{b}$ 的取值范围为（）．

A、 $[- 1 ， + \infty)$ B、 $[1 ， + \infty)$ C、 $(- \infty ， 1]$ D、 $[- 1 ， 0]$

查看试题解析
8. 已知函数 $f (x) = \frac{l n x}{x}$ ，直线 $l ： y = a (2 x - 1)$ ，若有且仅有一个整数 $x_{0}$ ，使得点 $P (x_{0} ， f (x_{0}))$ 在直线l上方，则实数a的取值范围是（）

A、 $[l n 2 ， l n 3)$ B、 $(l n 2 ， l n 3]$ C、 $[\frac{l n 3}{15} ， \frac{l n 2}{6})$ D、 $(\frac{l n 3}{15} ， \frac{l n 2}{6}]$

查看试题解析

二、多选题

9. 函数 $f (x)$ 的导函数 $f^{'} (x)$ 的图象如图所示，则下列说法正确的有（）

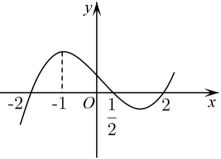A、 $x = - 2$ 为函数 $f (x)$ 的一个零点 B、 $x = \frac{1}{2}$ 为函数 $f (x)$ 的一个极大值点 C、函数 $f (x)$ 在区间 $(- 2 ， \frac{1}{2})$ 上单调递增 D、 $f (- 1)$ 是函数 $f (x)$ 的最大值

查看试题解析
10. 为了贯彻常态化疫情防控工作，动员广大医护人员抓细抓实各项防疫工作，人民医院组织护理、感染、儿科、疾控、药剂、呼吸六位专家进行“防疫有我，健康同行”知识讲座，每天一人，连续6天.则下列结论正确的是（）

A、从六位专家中选两位的不同选法共有20种 B、“呼吸类专家”不排在最后一天的不同排法共有600种 C、“护理、感染类专家”排在相邻两天的不同排法共有240种 D、“护理、感染、儿科类专家”排在都不相邻的三天的不同排法共有72种

查看试题解析
11. 已知函数 $f (x) = s i n (2 x + φ) (- \frac{π}{2} < φ < \frac{π}{2})$ 的图像关于直线 $x = \frac{π}{8}$ 对称，则（）

A、函数 $y = f (x)$ 的图像关于点 $(- \frac{π}{8} ， 0)$ 对称 B、函数 $y = f (x)$ 在 $[0 ， π]$ 有且仅有2个极值点 C、若 $| f (x_{1}) - f (x_{2}) | = 2$ ，则 $| x_{1} - x_{2} |$ 的最小值为 $\frac{π}{4}$ D、若 $f (α - \frac{π}{8}) f (β - \frac{π}{8}) = \frac{1}{2}$ ，则 $c o s 2 (α - β) = 1 + c o s 2 (α + β)$

查看试题解析
12. 已知函数 $f (x) = e^{x} l n (x + 1)$ ， $f^{'} (x)$ 是 $f (x)$ 的导数，则（）

A、函数 $y = f^{'} (x)$ 在 $(0 ， + ∞)$ 上单调递增 B、函数 $y = f^{'} (x)$ 有唯一极小值 C、函数 $y = f (x) - x$ 在 $(- 1 ， 0)$ 上有且只有一个零点 $t$ ，且 $t \in (- \frac{1}{2} ， 0)$ D、对于任意的 $x_{1}$ ， $x_{2} \in (0 ， + \infty)$ ， $f (x_{1} + x_{2}) > f (x_{1}) + f (x_{2})$ 恒成立

查看试题解析

三、填空题

13. 有 $3$ 男 $2$ 女共 $5$ 名学生被分派去 $A ， B ， C$ 三个公司实习，每个公司至少 $1$ 人，且 $A$ 公司要且只要 $1$ 个女生，共有种不同的分派方法.(用数字作答)

查看试题解析
14. 函数 $f (x) = x \cos x - \sin x$ 在区间 $[- π ， 0]$ 上的最大值为．

查看试题解析
15. 若 $A_{n + 1}^{2} - C_{n}^{n - 2} = 27$ ，则 $n =$ .

查看试题解析
16. 函数 $f (x)$ 的定义域为 $(- \infty ， + \infty)$ ，其导函数为 $f^{^{'}} (x)$ ，若 $f (x) = f (- x) - 2 s i n x$ ，且当 $x \geq 0$ 时， $f^{'} (x) > - c o s x$ ，则不等式 $f (x + \frac{π}{2}) > f (x) + s i n x - c o s x$ 的解集为．

查看试题解析

四、解答题

17. 已知函数 $f (x) = \frac{1}{3} x^{3} - 4 x + 2$ .

(1)、求函数 $f (x)$ 在 $x = 3$ 处的切线方程；

(2)、求函数 $f (x)$ 在 $[0 ， 3]$ 上的最大值与最小值.

查看试题解析
18. 已知数列 ${a_{n}}$ ， $\vec{x} = (a_{n + 1} ， - 2)$ ， $\vec{y} = (1 ， a_{n})$ ，且 $\vec{x} ⊥ \vec{y}$ ， $a_{3} + 2$ 是 $a_{2}$ 与 $a_{4}$ 的等差中项．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = 13 + 2 l o g_{\frac{1}{2}} a_{n}$ ， $S_{n} = b_{1} + b_{2} + \cdot \cdot \cdot + b_{n}$ ，求 $S_{n}$ 的最大值．

查看试题解析
19. 已知函数 $f (x) = x^{3} + 3 m x^{2} + n x$ 在 $x = - 1$ 时有极值0

(1)、求 $m ， n$ 的值；

(2)、求函数 $f (x)$ 的单调区间与极值.

查看试题解析
20. 为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用 $C$ （单位：万元）与隔热层厚度 $x$ （单位：cm）满足关系： $C (x) = \frac{40}{3 x + 5} (1 \leq x \leq 10)$ ，设 $f (x)$ 为隔热层建造费用与20年的能源消耗费用之和．

(1)、求 $f (x)$ 的表达式；

(2)、隔热层修建多厚时，总费用 $f (x)$ 达到最小，并求最小值．

查看试题解析
21. 已知函数 $f (x) = x^{2} - a l n x (a \in R)$ ，

(1)、讨论函数 $f (x)$ 的单调性；

(2)、若函数 $y = f (x)$ 在区间 $(1 ， e]$ 上存在两个不同零点，求实数 $a$ 的取值范围．

查看试题解析
22. 已知函数 $f (x) = \ln x - a x + 1$ ．

(1)、若 $f (x) \leq 0$ 恒成立，求实数 $a$ 的取值范围；

(2)、求证：当 $n \in N_{+}$ 时， $1 + \frac{1}{2} + \frac{1}{3} + \cdot \cdot \cdot + \frac{1}{n} + e > \ln (n + 1) + {(1 + \frac{1}{n})}^{n}$ 成立．

查看试题解析