江苏省泰州市姜堰区2022-2023学年七年级下学期期中数学试题

试卷更新日期：2023-05-12 类型：期中考试

进入出卷网下载

一、单选题

1. 下列生活中的现象，属于平移的是（）

A、摩天轮在运行 B、抽屉的拉开 C、坐在秋千上人的运动 D、树叶在风中飘落

查看试题解析
2. 如图是一杆秤在称物过程中某一时刻的状态，所有秤绳都平行．已知 $∠ 1 = 80 °$ ，则 $∠ 2$ 的度数是（）

A、 $80 °$ B、 $100 °$ C、 $120 °$ D、 $130 °$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} + a^{4} = a^{6}$ B、 ${(- a^{2})}^{3} = a^{6}$ C、 $a \cdot a^{5} = a^{6}$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
4. 小李想做一个三角形的框架，他有两根长度分别为 $12 c m$ 和 $10 c m$ 的细木条，需要将其中一根木条分为两段与另一根组成一个三角形．如果不考虑损耗和接头部分，那么小李应该选择把哪根木条分为两段？（）

A、 $12 c m$ 的木条 B、 $10 c m$ 的木条 C、两根都可以 D、两根都不行

查看试题解析
5. 如图是某一水库边的警示牌，牌面由正五边形（正五边形的每个内角都相等）和长方形组成，则 $∠ 1 + ∠ 2$ 的和是（）

A、 $36 °$ B、 $45 °$ C、 $60 °$ D、 $72 °$

查看试题解析
6. 若 $M = (x - 2) (x - 3) ， N = (x - 1) (x - 4)$ ，则M与N的大小关系是（）

A、由x的取值而定 B、 $M = N$ C、 $M < N$ D、 $M > N$

查看试题解析

二、填空题

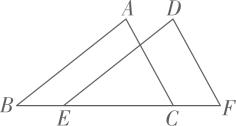
7. 六边形的外角和等于°.

查看试题解析
8. 每个生物携带自身基因的载体是生物细胞的 $D N A$ ． $D N A$ 分子的直径只有 $0.0000002 c m$ ，它们在细胞核的染色体上，按一定顺序排列成螺旋形的独特结构．将0.0000002用科学记数法表示是．

查看试题解析
9. 如图，将 $△ A B C$ 沿着 $B C$ 方向平移到 $△ D E F$ ．已知 $B C = 6 c m$ ， $E C = 4 c m$ ，那么平移的距离为 $c m$ ．

查看试题解析
10. 已知 $a^{m} = 16$ ， $a^{n} = 8$ ，则 $a^{m - n}$ 的值是．

查看试题解析
11. 一个正方体的棱长是1.5a，那么它的体积是．

查看试题解析
12. 已知 $x^{2} - x - 1 = 0$ ，则 $(x + 2) (3 - x)$ 的值是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ B A C$ 与 $∠ A C B$ 的角平分线相交于点P．若 $∠ A P C = 130 °$ ，则 $∠ B =$ $°$ ．

查看试题解析
14. 若 $(x + 2 a) (x^{2} + 3 x - 1)$ 的计算结果中不含x的一次项，则a的值是．

查看试题解析
15. 已知 $a = - (0.3)^{2} ， b = - 3^{- 2} ， c = {(- \frac{1}{3})}^{- 2} ， d = {(- \frac{1}{3})}^{0}$ ，则a、b、c、d的大小关系是．（用“>”号连接）

查看试题解析
16. 如图， $△ A B C$ 的中线 $A D$ 、 $B E$ 相交于点F， $F H ⊥ B C$ ，垂足为H．若 $S_{△ A B C} = 12$ ， $B C = 6$ ，则 $F H$ 长为．

查看试题解析

三、解答题

17. 计算：

(1)、 $m \cdot m^{2} + {(- m^{3})}^{2} \div m^{3}$

(2)、 ${(0.25)}^{10} \times 4^{10}$

(3)、 ${(- 2 x)}^{3} \cdot (x^{2} - 4 x + 3)$

(4)、 $(a + b + 1) (a + b - 1)$

查看试题解析
18. 用简便方法计算：

(1)、 $99 . 8^{2}$

(2)、 $199 \times 201 + 1$

查看试题解析
19. 先化简，再求值： $2 {(a - 2 b)}^{2} - (2 b + a) (- 2 b + a)$ ，其中 $a = - 1 ， b = - 2$ ．

查看试题解析
20. 如图，在方格纸内将 $△ A B C$ 经过一次平移后得到 $△ A^{'} B^{'} C^{'}$ ，点C的对应点为 $C^{'}$ ．根据下列条件，利用网格点和无刻度直尺画图．

(1)、画出平移后的 $△ A^{'} B^{'} C^{'}$ ；

(2)、连接 $A A^{'} 、 B B^{'}$ ，则 $A A^{'}$ 与 $B B^{'}$ 的数量与位置关系是；

(3)、在直线 $B C$ 的下方找一格点D，使得 $△ A B D$ 与 $△ A B C$ 的面积相等．

查看试题解析
21. 如图，在 $△ A B C$ 中，线段 $C D$ 是 $△ A B C$ 的高．给出下列三个选项：① $∠ 1 = ∠ 2$ ；② $∠ B = ∠ A D G$ ；③ $E F ⊥ A B$ ．从上述三个选项中任选两个作为条件，另一个作为结论，使结论成立，并说明理由．

已知： ▲ ，结论： ▲ ．（填序号）

理由：

查看试题解析
22. 观察下列等式
① $2 \times 2 - 1 \times 3 = 1$ ；

② $3 \times 3 - 2 \times 4 = 1$ ；

③ $4 \times 4 - 3 \times 5 = 1$ ；

…

(1)、仿照上面的式子，写出一个符合以上规律的式子是：；

(2)、试用字母表示上述式子的规律，并说明结论的正确性．

查看试题解析
23. 我国著名数学家华罗庚曾用诗词表达了“数形结合”的思想，其中谈到“数缺形时少直观，形少数时难入微．数形结合百般好，隔离分家万事休．”请你利用“数形结合”的思想解决以下问题：如图1是一个长 $4 a$ ，宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成如图2的图形．

(1)、观察图形，写出一个 $(a + b)^{2} 、 (a - b)^{2} 、 a b$ 三者之间的等量关系式是；

(2)、运用（1）中的结论，当 $x - y = 7 ， x y = - 6$ 时，求 $x + y$ 的值；

(3)、若 $(2022 - m) (2023 - m) = 4$ ，求 $(2022 - m)^{2} + (2023 - m)^{2}$ 的值．

查看试题解析
24. 如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ ，点P为线段 $A D$ 上一动点，过点P作 $P E ⊥ A D$ 交射线 $B C$ 于点E．

(1)、当 $∠ B = 30 ° ， ∠ A C B = 70 °$ 时，求 $∠ P E D$ 的度数；

(2)、当点P在线段 $A D$ 上运动时（点P与点A、点D不重合），设 $∠ P E D = α ， ∠ A C B = β ， ∠ B = γ (β > γ)$ ．猜想： $\frac{α}{β - γ}$ 的值是否变化？若不变，求出这个值；如变化，请说明理由．

查看试题解析
25. 阅读理解：由两个或两类对象在某些方面的相同或相似，得出它们在其他方面也可能相同或相似的推理方法叫类比法．多项式除以多项式可以类比于多位数的除法进行计算．
如：

$\begin{array}{l} 12 \begin{matrix} 23 \\ 278 \end{matrix} \\ \underline{24} \\ 38 \\ \underline{36} \\ 2 \end{array}$ $\begin{array}{l} x - 1 \begin{matrix} x^{2} + 3 x + 3 \\ x^{3} + 2 x^{2} + 0 \cdot x - 3 \end{matrix} \\ \underline{x^{3} - x^{2}} \\ \underline{\begin{array}{l} 3 x^{2} + 0 \cdot x \\ 3 x^{2} - 3 x \end{array}} \\ \underline{\begin{array}{l} 3 x - 3 \\ 3 x - 3 \end{array}} \\ 0 \end{array}$

$∴ 278 \div 12 = 232$ $∴ (x^{3} + 2 x^{2} - 3) \div (x - 1) = x^{2} + 3 x + 3$

即多项式除以多项式用竖式计算，步骤如下：

①把被除式和除式按同一字母的指数从大到小依次排列（若有缺项用零补齐）．

②用竖式进行运算．

③当余式的次数低于除式的次数时，运算终止，得到商式和余式．若余式为零，说明被除式能被除式整除．

例如： $(x^{3} + 2 x^{2} - 3) \div (x - 1) = x^{2} + 3 x + 3$

$∵$ 余式为0

$∴ x^{3} + 2 x - 3$ 能被 $x - 1$ 整除．

根据阅读材料，请回答下列问题：

(1)、多项式 $x^{2} + 5 x + 6$ 除以多项式 $x + 2$ ，所得的商式为；

(2)、已知关于x的二次多项式除以 $x + 1$ ，商式是 $2 x - 2$ ，余式是-1，求这个多项式；

(3)、已知 $x^{3} + 2 x^{2} - a x - 10$ 能被 $x - 2$ 整除，则 $a =$ ；

(4)、如图，有2张A卡片，3张B卡片，1张C卡片，能否将这6张卡片拼成一个与原来总面积相等且一边长为 $(a + b)$ 的长方形？若能，求出另一边长；若不能，请说明理由．

查看试题解析
26. 综合与实践——折纸中的数学
折纸是同学们喜欢的手工活动之一，通过折纸我们可以得到许多美丽的图形，折纸的过程还蕴含着丰富的数学知识．将长方形纸片（长方形的对边平行且相等，四个内角都是直角），按下列要求折叠．

(1)、如图1，将长方形纸条沿直线 $E F$ 折叠，点C落在 $C^{'}$ 处，点D落在 $D^{'}$ 处， $C^{'} F$ 交 $A D$ 于点G．
①若 $∠ 1 = 35 °$ ，则 $∠ A G C^{'} =$ ▲ ；
②若 $∠ A G C^{'} = 3 ∠ 1$ ，求 $∠ A G C^{'}$ 的度数．

(2)、在图1的基础上，将四边形 $A B F G$ 沿某一直线折叠，使得 $A G$ 或 $B F$ 落在直线 $G F$ 上，折痕为 $M N$ ，则折痕 $M N 、 E F$ 有怎样的位置关系，并说明理由．

(3)、若 $A B = 3 ， B C = 12$ ，按图2方式折叠，点 $C^{'} 、 G 、 F 、 A^{'}$ 在一条直线上．若四边形 $B^{'} A^{'} F H$ 的面积记为 $S_{1}$ ，四边形 $D^{'} E G C^{'}$ 的面积记为 $S_{2}$ ，则 $S_{1} + S_{2}$ 的值是否有最大值？若有，求出这个值；若没有，请说明理由．

查看试题解析