2023年河南省中考数学模拟卷
试卷更新日期:2023-05-12 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 在下列各数:3.14,-π, , 、、中无理数的个数是( )A、2 B、3 C、4 D、52. 数轴上,有理数a、b、-a、c的位置如图,则化简的结果为( )
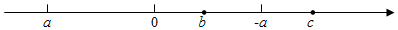 A、 B、 C、 D、03. 如果与是同类项,则的值为( )A、4 B、-4 C、8 D、124. 如图,直线AB、CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=50°,则∠AOC= ( )
A、 B、 C、 D、03. 如果与是同类项,则的值为( )A、4 B、-4 C、8 D、124. 如图,直线AB、CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=50°,则∠AOC= ( )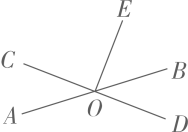 A、140° B、50° C、60° D、40°5. 如图所示, , , 下列说法错误的是( )
A、140° B、50° C、60° D、40°5. 如图所示, , , 下列说法错误的是( ) A、点B到AC的垂线段是线段AB B、点C到AB的垂线段是线段AC C、线段AD是点D到BC的垂线段 D、线段BD是点B到AD的垂线段6. 下列计算正确的是( )A、 B、 C、 D、7. 2022年,新型冠状肺炎病毒奥密克戎变异毒株影响全球,各国感染人数持续攀升,该企业决定增加甲、乙两个厂房生产型医用口罩,甲厂房每天生产的数量是乙厂房每天生产数量的2倍;两厂房各加工箱型医用口罩,甲厂房比乙厂房少用5天.设乙厂房每天生产x箱型医用口罩.根据题意可列方程为( )A、 B、 C、 D、8. 我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式 , 请结合你所学知识,判断下列说法:①当时,;②无论a取任何实数,不等式恒成立;③若 , 则.正确的有( )A、3个 B、2个 C、1个 D、0个9. 开学前,根据学校防疫要求,小宁同学连续14天进行了体温测量,结果统计如下表:
A、点B到AC的垂线段是线段AB B、点C到AB的垂线段是线段AC C、线段AD是点D到BC的垂线段 D、线段BD是点B到AD的垂线段6. 下列计算正确的是( )A、 B、 C、 D、7. 2022年,新型冠状肺炎病毒奥密克戎变异毒株影响全球,各国感染人数持续攀升,该企业决定增加甲、乙两个厂房生产型医用口罩,甲厂房每天生产的数量是乙厂房每天生产数量的2倍;两厂房各加工箱型医用口罩,甲厂房比乙厂房少用5天.设乙厂房每天生产x箱型医用口罩.根据题意可列方程为( )A、 B、 C、 D、8. 我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式 , 请结合你所学知识,判断下列说法:①当时,;②无论a取任何实数,不等式恒成立;③若 , 则.正确的有( )A、3个 B、2个 C、1个 D、0个9. 开学前,根据学校防疫要求,小宁同学连续14天进行了体温测量,结果统计如下表:体温
36.2
36.3
36.5
36.6
36.8
天数天
3
3
4
2
2
这14天中,小宁体温的众数和中位数分别为( )
A、 , B、 , C、 , D、 ,10. 如图,抛物线与轴正半轴交于两点(点在点的左边),与轴正半轴交于 , 且 , 则点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共15分)
-
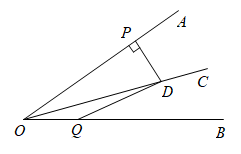
11. 若与3互为相反数,则等于.12. 已知关于x的方程与的解相同,则.13. 若m是方程的一个根,则的值为.14. 如图,射线是的角平分线,是射线上一点,于点 , , 若点是射线上一点, , 则的面积是.
 15. 如图,是的直径,弦与相交于点 , 若 , , , 则到的距离为.
15. 如图,是的直径,弦与相交于点 , 若 , , , 则到的距离为.
三、计算题(共10分)
-
16. 计算:(1)、(2)、
四、解答题(共7题,共65分)
-
17. 先化简,再求值: , 其中 , .18. 某校对甲,乙两人的射击成绩进行了测试,测试成绩如表:
第一次
第二次
第三次
第四次
第五次
甲命中环数
7
8
8
8
9
乙命中环数
10
6
10
6
8
(1)、分别求出甲,乙两人射击成绩的平均数和方差;(2)、现要从甲,乙两人中选拔一人参加比赛,你认为挑选哪一位较合适,请说明理由.19. 如图,在中, , 是的平分线,于E. (1)、求证:;(2)、若 , 求的周长.20. 已知关于x的一元二次方程x2+(m-3)x-3m=0.(1)、求证:这个一元二次方程一定有两个实数根;(2)、设该一元二次方程的两根为a、b,且2、a、b分别是一个直角三角形的三边长,求m的值.21. 某村在政府的扶持下建起了鲜花大棚基地,准备种植 , 两种鲜花。经测算,种植两种鲜花每亩的投入与获利情况如下表:
(1)、求证:;(2)、若 , 求的周长.20. 已知关于x的一元二次方程x2+(m-3)x-3m=0.(1)、求证:这个一元二次方程一定有两个实数根;(2)、设该一元二次方程的两根为a、b,且2、a、b分别是一个直角三角形的三边长,求m的值.21. 某村在政府的扶持下建起了鲜花大棚基地,准备种植 , 两种鲜花。经测算,种植两种鲜花每亩的投入与获利情况如下表:每亩需投入(万元)
每亩可获利(万元)
种鲜花
2
0.8
种鲜花
4
1.2
(1)、政府和村共同投入200万元全部用来种植这两种鲜花,总获利万元.设种植种鲜花亩,求关于的函数关系式;(2)、在(1)的条件下,若要求A种鲜花的种植面积不能多于B种鲜花种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
-

