陕西省宝鸡市凤翔区2023年中考数学模拟试卷
试卷更新日期:2023-05-12 类型:中考模拟
一、单选题
-
1. 如图,直角三角板 的直角顶点 在直线 上,若 , ,则 ( )
 A、30° B、40° C、50° D、60°2. ﹣6的相反数是( )A、﹣6 B、﹣ C、6 D、3. 下列计算中,结果与相等的是( )A、 B、 C、 D、4. 将直线向下平移2个单位长度,得到的直线解析式为( )A、 B、 C、 D、5. 如图,A、B、C是半径为3的上的三点,已知 , 则弦AB的长为( )
A、30° B、40° C、50° D、60°2. ﹣6的相反数是( )A、﹣6 B、﹣ C、6 D、3. 下列计算中,结果与相等的是( )A、 B、 C、 D、4. 将直线向下平移2个单位长度,得到的直线解析式为( )A、 B、 C、 D、5. 如图,A、B、C是半径为3的上的三点,已知 , 则弦AB的长为( )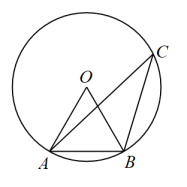 A、3 B、6 C、3.5 D、1.56. 某班有若干个活动小组,其中书法小组人数的3倍比绘画小组的人数多15人,绘画小组人数的2倍比书法小组的人数多5人,问:书法小组和绘画小组各有多少人?若设书法小组有x人,绘画小组有y人,那么可列方程组为( )A、 B、 C、 D、7. 已知如图,、是的弦,与坐标系x、y轴交于B、A两点,点A的坐标为 , 的弦的长为 , 则的度数为( )
A、3 B、6 C、3.5 D、1.56. 某班有若干个活动小组,其中书法小组人数的3倍比绘画小组的人数多15人,绘画小组人数的2倍比书法小组的人数多5人,问:书法小组和绘画小组各有多少人?若设书法小组有x人,绘画小组有y人,那么可列方程组为( )A、 B、 C、 D、7. 已知如图,、是的弦,与坐标系x、y轴交于B、A两点,点A的坐标为 , 的弦的长为 , 则的度数为( )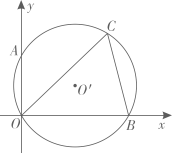 A、 B、 C、 D、8. 如图,抛物线 的顶点为B(1,3),与 轴的交点A在点 (2,0)和(3,0)之间.以下结论:
A、 B、 C、 D、8. 如图,抛物线 的顶点为B(1,3),与 轴的交点A在点 (2,0)和(3,0)之间.以下结论:① ;② ;③ ;④ ≥ ;⑤若 ,且 ,
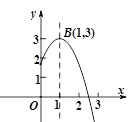
则 .其中正确的结论有( )
A、4个 B、3个 C、2个 D、1个二、填空题
-
9. 比较下列两数大小: .10. 如图,在△ABC中,AB=AC , ∠B=60°,AD平分∠BAC , 点E是线段BC延长线上一点,连接AE , 点C在AE的垂直平分线上,若CE=8cm,则AB+BD=cm.
 11. 如图,四边形的顶点都在坐标轴上,若 , 与面积分别为12和27,若双曲线恰好经过的中点 , 则的值为 .
11. 如图,四边形的顶点都在坐标轴上,若 , 与面积分别为12和27,若双曲线恰好经过的中点 , 则的值为 . 12. 如图,中, , , 以边上的中线为折痕将折叠,使点A落在点D处,如果恰好与垂直,则的值为 .
12. 如图,中, , , 以边上的中线为折痕将折叠,使点A落在点D处,如果恰好与垂直,则的值为 .
三、解答题
-
13.(1)、计算:(2)、化简:14. 计算:(1)、;(2)、.15. 解不等式组 .16. 已知:在正方形ABCD中,点M是CD边上的任意一点,BE⊥AM于点E , DF⊥AM于点F .
 (1)、求证:ADF≌BAE;(2)、如果正方形ABCD的边长为10,DF=6,求EF的长.17. 如图,AB为的切线,B为切点,过点B作 , 垂足为点E,交于点C,延长CO与AB的延长线交于点D.
(1)、求证:ADF≌BAE;(2)、如果正方形ABCD的边长为10,DF=6,求EF的长.17. 如图,AB为的切线,B为切点,过点B作 , 垂足为点E,交于点C,延长CO与AB的延长线交于点D.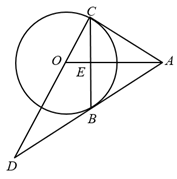 (1)、求证:AC为的切线;(2)、若 , , 求线段AD的长.18. 在数学活动课上,九年级(1)班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离,现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东42°方向,测得点P与亭子A之间的距离为200米,求亭子A与亭子B之间的距离.(结果精确到1米)
(1)、求证:AC为的切线;(2)、若 , , 求线段AD的长.18. 在数学活动课上,九年级(1)班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的亭子B之间的距离,现测得亭子A位于点P北偏西30°方向,亭子B位于点P北偏东42°方向,测得点P与亭子A之间的距离为200米,求亭子A与亭子B之间的距离.(结果精确到1米)【参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90, =1.73】
 19. 在“六一国际儿童节”来临之际,某校开展了向山区“希望小学”捐赠图书活动.全校1000名学生每人都捐赠了一定数量的图书,已知各年级人数分布的扇形统计图如图⑴所示.学校为了了解各年级捐赠图书情况,从各年级中随机抽查了部分学生,进行捐赠图书情况的统计,绘制成如图⑵的频数分布直方图.
19. 在“六一国际儿童节”来临之际,某校开展了向山区“希望小学”捐赠图书活动.全校1000名学生每人都捐赠了一定数量的图书,已知各年级人数分布的扇形统计图如图⑴所示.学校为了了解各年级捐赠图书情况,从各年级中随机抽查了部分学生,进行捐赠图书情况的统计,绘制成如图⑵的频数分布直方图.根据以上信息解答下列问题:
 (1)、人均捐赠图书最多的是年级;(2)、估计九年级学生共捐赠图书多少册?(3)、全校大约共捐赠图书多少册?20. 已知: 中, 为 上的中线,点E在 上,且 ,射线 交 于点F.求 的值.
(1)、人均捐赠图书最多的是年级;(2)、估计九年级学生共捐赠图书多少册?(3)、全校大约共捐赠图书多少册?20. 已知: 中, 为 上的中线,点E在 上,且 ,射线 交 于点F.求 的值.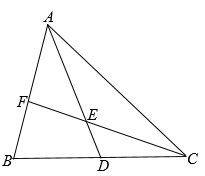 21. 如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量 (千瓦时)关于已行驶路程 (千米)的函数图象.
21. 如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量 (千瓦时)关于已行驶路程 (千米)的函数图象.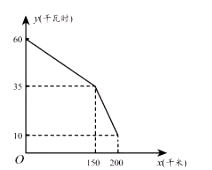 (1)、根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当 时,求1千瓦时的电量汽车能行驶的路程;(2)、当 时求 关于 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.22. 兴城泳装在国内外享有较高的知名度,网店经销某品牌泳装,每件成本30元,网店按单价不低于成本,且不高于50元销售.在销售过程中发现,泳装每天的销售量 (件)与销售单价 (元)之间满足一次函数关系,其图象如图所示.
(1)、根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当 时,求1千瓦时的电量汽车能行驶的路程;(2)、当 时求 关于 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.22. 兴城泳装在国内外享有较高的知名度,网店经销某品牌泳装,每件成本30元,网店按单价不低于成本,且不高于50元销售.在销售过程中发现,泳装每天的销售量 (件)与销售单价 (元)之间满足一次函数关系,其图象如图所示. (1)、求该泳装每天的销售量 (件)与 (元)之间的函数关系式;(2)、当每件泳装的售价为多少元时,每天销售泳装获得的利润为1050元?(3)、销售单价定为多少元时,才能使每天销售泳装获得的利润 (元)最大?最大利润是多少元?23. 如图,有两部不同型号的手机(分别记为A,B)和与之匹配的2个保护盖(分别记为a,b)散乱地放在桌子上.
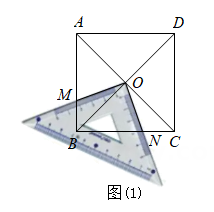
(1)、求该泳装每天的销售量 (件)与 (元)之间的函数关系式;(2)、当每件泳装的售价为多少元时,每天销售泳装获得的利润为1050元?(3)、销售单价定为多少元时,才能使每天销售泳装获得的利润 (元)最大?最大利润是多少元?23. 如图,有两部不同型号的手机(分别记为A,B)和与之匹配的2个保护盖(分别记为a,b)散乱地放在桌子上. (1)、若从手机中随机取一部,再从保护盖中随机取一个,求恰好匹配的概率;(2)、若从手机和保护盖中随机取两个,用画树状图法或列表法求恰好匹配的概率.24. 已知△ABC的两边AB、AC的长是关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0的两个实数根,第三边BC的长为5,试问:k取何值时,△ABC是以BC为斜边的直角三角形?25. 数学学习小组“陆月辉煌”最近正在进行几何图形组合问题的研究.认真研读以下四个片段,并回答问题.(1)、【片段一】小陆说:将一块足够大的等腰直角三角板置于一个正方形中,直角顶点与对角线交点O重合,在转动三角板的过程中我发现某些线段之间存在确定的数量关系.
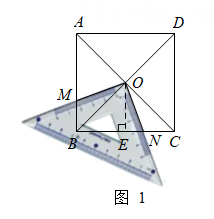
(1)、若从手机中随机取一部,再从保护盖中随机取一个,求恰好匹配的概率;(2)、若从手机和保护盖中随机取两个,用画树状图法或列表法求恰好匹配的概率.24. 已知△ABC的两边AB、AC的长是关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0的两个实数根,第三边BC的长为5,试问:k取何值时,△ABC是以BC为斜边的直角三角形?25. 数学学习小组“陆月辉煌”最近正在进行几何图形组合问题的研究.认真研读以下四个片段,并回答问题.(1)、【片段一】小陆说:将一块足够大的等腰直角三角板置于一个正方形中,直角顶点与对角线交点O重合,在转动三角板的过程中我发现某些线段之间存在确定的数量关系.如图(1),若三角板两条直角边的外沿分别交正方形的边AB、BC于点M、N , 则①OM+ON=MB+NB;② .
请你判断他的猜想是否正确?并证明你认为正确的猜想.
 (2)、【片段二】小月说:将三角板中一个45°角的顶点和正方形的一个顶点重合放置,使得这个角的两条边与正方形的一组邻边有交点.
(2)、【片段二】小月说:将三角板中一个45°角的顶点和正方形的一个顶点重合放置,使得这个角的两条边与正方形的一组邻边有交点.如图(2),若以A为顶点的45°角的两边分别交正方形的边BC、CD于点M、N , 交对角线BD于点E、F . 我发现:BE2+DE2=2AE2 , 只要准确旋转图(2)中的一个三角形就能证明这个结论.
请你写出小月所说的具体的旋转方式: .
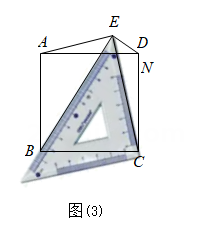
 (3)、【片段三】小辉说:将三角板的一个45°角放置在正方形的外部,同时角的两边恰好经过正方形两个相邻的顶点.
(3)、【片段三】小辉说:将三角板的一个45°角放置在正方形的外部,同时角的两边恰好经过正方形两个相邻的顶点.如图(3),设顶点为E的45°角位于正方形的边AD上方,这个角的两边分别经过点B、C , 连接EA , ED . 那么线段EB、EC、ED也存在确定的数量关系:(EB+ED)2=2EC2 .
请你证明这个结论.
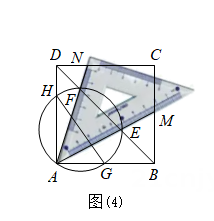
 (4)、【片段四】小煌说:在图(2)中,作一个过点A、E、F的圆,交正方形的边AB、AD于点G、H , 如图(4)所示.你知道线段DH、HG、GB三者之间的关系吗?请直接写出结论: .
(4)、【片段四】小煌说:在图(2)中,作一个过点A、E、F的圆,交正方形的边AB、AD于点G、H , 如图(4)所示.你知道线段DH、HG、GB三者之间的关系吗?请直接写出结论: .