陕西省宝鸡市凤翔区2022-2023学年七年级下学期期中地数学试卷

试卷更新日期：2023-05-12 类型：期中考试

进入出卷网下载

一、单选题

1. 芝麻的用途广泛，经测算，一粒芝麻约有0. 00000201千克. 数据0. 00000201用科学记数法表示为（）

A、 $0.201 \times 10^{- 5}$ B、 $2.01 \times 10^{- 5}$ C、 $2.01 \times 10^{- 6}$ D、 $20.1 \times 10^{- 7}$

查看试题解析
2. 下列运算正确的是（）

A、 $3 a b - a b = 3$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 $a \div a^{- 1} = 1 (a \neq 0)$ D、 ${(- 3 a^{2} b)}^{2} = 9 a^{4} b^{2}$

查看试题解析
3. 如图，在乡村振兴活动中，某村通过铺设水管将河水引到村庄C处，为节省材料，他们，垂足为点D，于是确定沿 $C D$ 铺设水管，这样做的数学道理是（）

A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、平面内过一点有且只有一条直线与已知直线垂直

查看试题解析
4. 二十四节气是中国古代劳动人民长期经验积累的结晶，它与白昼时长密切相关．当春分、秋分时，昼夜时长大致相等；当夏至时，白昼时长最长，根据如图，在下列选项中指出白昼时长不足11小时的节气（）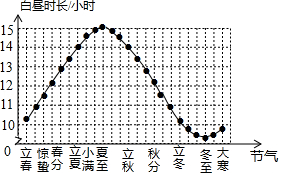

A、惊蛰 B、小满 C、立秋 D、大寒

查看试题解析
5. 如图， $∠ 1 = 70 °$ ， $∠ 2 = 160 °$ 直线a平移后得到直线b，则 $∠ 3 =$ （）

A、20° B、30° C、40° D、50°

查看试题解析
6. 某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据

温度/℃

﹣20

﹣10

0

10

20

30

声速/m/s

318

324

330

336

342

348

下列说法错误的是（）

A、这个问题中，空气温度和声速都是变量 B、空气温度每降低10℃，声速减少6m/s C、当空气温度为20℃时，声音5s可以传播1710m D、由数据可以推测，在一定范围内，空气温度越高，声速越快

查看试题解析
7. 若 $a 、 b$ 是某长方形的长和宽，且有 $(a + b)^{2} = 16 ， (a - b)^{2} = 4$ ，则该长方形面积为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 如图所示，若AB∥EF，则∠B，∠C，∠E之间的度数关系是（）

A、∠E+∠C-∠B＝180° B、∠E+∠C+∠B＝180° C、∠E-∠C-∠B＝90 D、∠E-∠C+∠B＝O°

查看试题解析
9. 已知 $3^{m} = x$ ， $9^{n} = y$ ， $m$ 、 $n$ 为正整数，则 $3^{m + 2 n} =$ （）

A、 $x y$ B、 $x y^{2}$ C、 $x + y^{2}$ D、 $24 x y$

查看试题解析
10. 计算 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) ⋯ (2^{64} + 1)$ ，结果的个位数字是（）

A、6 B、5 C、8 D、7

查看试题解析

二、填空题

11. 计算： ${(- \frac{1}{2})}^{- 1}$ = ．

查看试题解析
12. 如图，已知 $A B ∥ D E$ ，且∠C=110°，则∠1与∠2的数量关系为 .

查看试题解析
13. 如果关于 $x$ 的多项式 $x^{2} + 8 x + b$ 是一个完全平方式，那么 $b =$

查看试题解析
14. 学校七年级开展种植班树活动．已知一班的班树现在高80厘米，以后一年中每个月平均长高2厘米，x月后这棵树的高度为h厘米，则h与x的函数关系式为．

查看试题解析
15. 如图所示的长方形纸条ABCD，将纸片沿MN折叠，MB与DN交于点K，若∠1＝70°，则∠MKN＝°．

查看试题解析

三、解答题

16. 计算：

(1)、 $1 0^{7} \div (1 0^{3} \div 1 0^{2})$

(2)、 ${(x + 2)}^{2} - (x + 1) (x - 1)$

查看试题解析
17. 化简求值： $[{(2 x - y)}^{2} - (x - y) (x + y) - 2 y^{2}] ÷ x$ ，其中 $x = 2$ ， $y = - 3$ ．

查看试题解析
18. 已知∠α，∠β，求作一个角∠AOB，使它等于∠α与∠β的和．
（要求：不在原图上作图，不写作法，保留作图痕迹）

查看试题解析
19. 如图，

(1)、∵∠A=      ▲      (已知)，
∴AC∥ED(同位角相等，两直线平行)

(2)、∵∠2=      ▲      (已知)，
∴AC∥ED（）

(3)、∵∠A+      ▲      =180°(已知)，
∴AB∥FD（）

(4)、∵AB∥      ▲      (已知)，
∴∠2+∠AED=180°（）

(5)、∵AC∥      ▲      (已知)，
∴∠C=∠1（）

查看试题解析
20. 如果 $m^{2} - m = 1$ ，求代数式 ${(m - 1)}^{2} + (m + 1) (m - 1) + 2022$ 的值．

查看试题解析
21. 聪聪和同学们用2张 $A$ 型卡片、2张 $B$ 型卡片和1张 $C$ 型卡片拼成了如图所示的长方形．其中 $A$ 型卡片是边长为 $a$ 的正方形； $B$ 型卡片是长方形； $C$ 型卡片是边长为 $b$ 的正方形．

(1)、请用含a、b的代数式分别表示出 $B$ 型卡片的长和宽；

(2)、如果 $a = 10$ ， $b = 6$ ，请求出他们用5张卡片拼出的这个长方形的面积．

查看试题解析
22. 如图，直线 $A B$ ， $C D$ 被直线 $B F$ 所截， $∠ A E F + ∠ C F E = 180 °$ ， $G F$ 平分 $∠ D F E$ ，交 $A B$ 于点 $G$ ， $∠ 1 = 58 °$ ，求 $∠ 2$ 的度数．

查看试题解析
23. 小明某天上午9时骑自行车离开家，15时回到家，他有意描绘了离家的距离与时间的变化情况（如图所示）．

(1)、图像表示了哪两个变量之间的关系？哪个是自变量？哪个是因变量？

(2)、10时和13时，他分别离家多远？

(3)、他到达离家最远的地方是什么时间？离家多远？

(4)、他可能在哪段时间内休息，并吃午餐？

查看试题解析
24. 如图，点D、E在AB上，点F、G分别在BC、CA上，且 $D G ∥ B C$ ， $∠ C D G = ∠ E F B$ .

(1)、试判断直线EF与直线CD的位置关系，并说明理由；

(2)、若 $E F ⊥ A B$ ， $∠ C D G = 56 °$ ，求 $∠ A D G$ 的度数.

查看试题解析
25. 光线照射到镜面会产生反射现象，由光学知识，入射光线与镜面的夹角与反射光线与镜面的夹角相等，例如：在图1中，有∠1＝∠2．

(1)、如图2，已知镜子MO与镜子ON的夹角∠MON＝90°，请判断入射光线AB与反射光线CD的位置关系，并说明理由；

(2)、如图3，有一口井，已知入射光线AO与水平线OC的夹角为50°，当平面镜MN与水平线OC的夹角为°，能使反射光线OB正好垂直照射到井底；

(3)、如图4，直线EF上有两点A、C，分别引两条射线AB、CD．∠BAF＝120°，∠DCF＝40°，射线AB、CD分别绕A点、C点以3度/秒和1度/秒的速度同时逆时针转动，设时间为t秒，在射线AB转动一周的时间内，是否存在某时刻，使得CD与AB平行？若存在，求出所有满足条件的时间t．

查看试题解析

温度/℃	﹣20	﹣10	0	10	20	30
声速/m/s	318	324	330	336	342	348