江苏省常州市金坛区2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-05-12 类型:期中考试
一、单选题
-
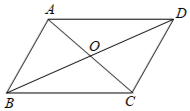
1. 下列成语所描述的事件属于不可能事件的是( )A、水落石出 B、水涨船高 C、水滴石穿 D、水中捞月2. 在一个不透明的布袋内,有10个红球,3个黄球,2个白球,1个蓝球,除颜色外其他都相同.若随机从袋中摸出1个球,则摸到可能性最大的是( )A、红球 B、黄球 C、白球 D、蓝球3. 如图,的对角线 , 相交于点O,下列等式一定正确的是( )
 A、 B、 C、 D、4. 如图,在中,连接 , , , 则的度数是( )
A、 B、 C、 D、4. 如图,在中,连接 , , , 则的度数是( )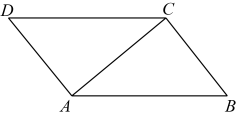 A、 B、 C、 D、5. 如图, 的对角线 , 交于点O,若 , ,则 的长可能是( )
A、 B、 C、 D、5. 如图, 的对角线 , 交于点O,若 , ,则 的长可能是( )
 A、10 B、8 C、7 D、66. 在下列条件中,能够判定为矩形的是( )A、 B、 C、 D、7. 如图,菱形的边长为2, , 则菱形的面积是( )
A、10 B、8 C、7 D、66. 在下列条件中,能够判定为矩形的是( )A、 B、 C、 D、7. 如图,菱形的边长为2, , 则菱形的面积是( )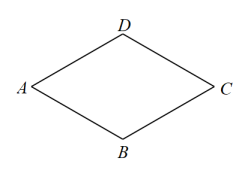 A、 B、 C、 D、8. 如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( )
A、 B、 C、 D、8. 如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( ) A、4 B、3 C、 D、2
A、4 B、3 C、 D、2二、填空题
-
9. 将40个数据分成5组,其中一组的频数是8,这组的频率是 .10. 为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,征求了所有学生的意见,赞成、反对、无所谓三种意见的人数之比为 , 为描述三种意见占总体的百分比,应选择统计图(填“条形”、“扇形”或“折线”).11. 如图,四边形是平行四边形,其中点 , 点 , 点 , 则点D的坐标是 .
 12. 已知菱形的两条对角线 , 则菱形的边长 .13. 如图,在正方形中,点E,F分别在边上, , , 则 .
12. 已知菱形的两条对角线 , 则菱形的边长 .13. 如图,在正方形中,点E,F分别在边上, , , 则 . 14. 若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是15. 如图,把矩形纸片沿对角线折叠,若 , , 则的面积是 .
14. 若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是15. 如图,把矩形纸片沿对角线折叠,若 , , 则的面积是 . 16. 如图,在中, , , , P为边上任意一点(点P与点C不重合),连接 , 以 , 为邻边作 , 连接 , 则长的最小值是 .
16. 如图,在中, , , , P为边上任意一点(点P与点C不重合),连接 , 以 , 为邻边作 , 连接 , 则长的最小值是 .
三、解答题
-
17. 某区为了解八年级学生视力健康状况,在全区随机抽查了部分八年级学生2021年末的视力数据,并根据调查结果绘制成如下统计图.
青少年视力健康标准
类别
视力
健康状况
A
视力≥5.0
视力正常
B
视力=4.9
轻度视力不良
C
4.6≤视力≤4.8
中度视力不良
D
视力≤4.5
重度视力不良
 (1)、本次调查的样本容量是;(2)、补全条形统计图;(3)、已知该区2021年末有八年级学生6000人,请估计该区八年级学生2021年末视力不良的人数.18. 某批乒乓球的质量检验结果如下:
(1)、本次调查的样本容量是;(2)、补全条形统计图;(3)、已知该区2021年末有八年级学生6000人,请估计该区八年级学生2021年末视力不良的人数.18. 某批乒乓球的质量检验结果如下:抽取的乒乓球数n
200
400
600
800
1000
1600
2000
优等品的频数m
190
384
570
756
955
1520
1900
优等品的频率
a
0.96
0.95
0.945
b
0.95
c
(1)、填空: , , ;(2)、在下图中画出优等品频率的折线统计图: (3)、从这批乒乓球中,任意抽取的一只乒乓球是优等品的概率的估计值是多少?19. 已知:如图,矩形的对角线、相交于点O, , .
(3)、从这批乒乓球中,任意抽取的一只乒乓球是优等品的概率的估计值是多少?19. 已知:如图,矩形的对角线、相交于点O, , . (1)、求的度数;(2)、求矩形对角线的长.20. 如图,E是正方形边延长线上的一点,且 .
(1)、求的度数;(2)、求矩形对角线的长.20. 如图,E是正方形边延长线上的一点,且 . (1)、求的度数;(2)、若 , 求的面积.21. 如图,已知 .
(1)、求的度数;(2)、若 , 求的面积.21. 如图,已知 . (1)、用直尺和圆规作图,作的平分线 , 交边于点E,在上方作 , 使得 , 交边于点F.(不写作法,保留作图痕迹,标注字母)(2)、在(1)的条件下,四边形是怎样的特殊四边形?证明你的结论.22. 如图,在中,D是边上一点,E是的中点,过C作 , 交的延长线于点F.
(1)、用直尺和圆规作图,作的平分线 , 交边于点E,在上方作 , 使得 , 交边于点F.(不写作法,保留作图痕迹,标注字母)(2)、在(1)的条件下,四边形是怎样的特殊四边形?证明你的结论.22. 如图,在中,D是边上一点,E是的中点,过C作 , 交的延长线于点F. (1)、求证:;(2)、连接 . 如果D是的中点,那么当与满足什么条件时,四边形是矩形?证明你的结论.
(1)、求证:;(2)、连接 . 如果D是的中点,那么当与满足什么条件时,四边形是矩形?证明你的结论.