浙江省台州市黄岩区2023年中考一模数学试题

试卷更新日期：2023-05-12 类型：中考模拟

进入出卷网下载

一、单选题

1. 在0，1，-2，3这四个数中，最小的数是（）

A、0 B、1 C、-2 D、3

查看试题解析
2. 2022年北京冬奥会3个赛区场馆使用绿色电力，减排320000吨二氧化碳．数字320000用科学记数法表示是（）

A、 $3.2 \times 10^{6}$ B、 $3.2 \times 10^{5}$ C、 $3.2 \times 10^{4}$ D、 $32 \times 10^{4}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{5}$ B、 ${(a^{4})}^{2} = a^{6}$ C、 $a + 2 a = 3 a^{2}$ D、 $a^{3} + a^{4} = a^{7}$

查看试题解析
4. 如图是由4个相同的小立方体搭成的几何体，则它的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 荸荠口感脆甜，营养丰富，黄岩院桥素有“店头荸荠三根葱”的美誉．某校兴趣小组对50株荸荠的叶状茎生长度进行测量、记录，统计如下表：

株数（株）

$7$

$12$

$23$

$8$

叶状茎长度（cm）

$45.6$

$46.5$

$46.9$

$47.8$

这批荸荠叶状茎长度的众数为（）

A、45.6 B、46.5 C、46.9 D、47.8

查看试题解析
6. 下列关于反比例函数 $y = - \frac{3}{x}$ 的描述中，正确的是（）

A、图象位于第二、四象限 B、图象过点（1，3） C、y随x的增大而增大 D、当 $x > - 1$ 时， $y > 3$

查看试题解析
7. 下列说法错误的是（）

A、对角线互相平分的四边形是平行四边形 B、四个角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、对角线垂直且相等的四边形是正方形

查看试题解析
8. 神舟十五号载人飞船搭载3名宇航员于2022年11月29日进入太空，在中国空间站进行了很多空间实验，计划今年6月返回．太空中水资源有限，要通过回收水的方法制造可用水，即将宇航员的汗液、尿液和太空水收集起来，经过特殊的净水器处理成可用水循环使用．净化水的过程中，每增加一次过滤可减少水中的杂质 $x %$ ，经过2次过滤可使水中的杂质减少到原来的 $64 %$ ，根据题意可列方程为（）

A、 $1 - 2 x = 64 %$ B、 ${(1 - x)}^{2} = 64 %$ C、 $2 (1 - x %) = 64 %$ D、 ${(1 - x %)}^{2} = 64 %$

查看试题解析
9. 如图，学校为美化校园环境，决定在一个边长为10m的正方形花坛中，按图中所示的分布方式种植郁金香和雏菊．则种植郁金香的总面积是（）

A、 $32 m^{2}$ B、 $40 m^{2}$ C、 $48 m^{2}$ D、 $50 m^{2}$

查看试题解析
10. 某娱乐设施每次能够容纳4人一组进场游玩，甲、乙、丙、丁排队等候，甲前面有若干人，乙排在甲后面，中间隔着2人，丙排在乙后面，中间隔着1人，丁排在丙后面，中间隔着1人，丁后面也有若干人．下列说法：①如果甲和乙同一组，那么丙和丁也同一组；②如果甲和乙不同一组，那么丙和丁也不同一组；③如果丙和丁同一组，那么甲和乙也同一组；④如果丙和丁不同一组，那么甲和乙也不同一组．正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 因式分解: $x^{2} - 16 =$ .

查看试题解析
12. 如图，五线谱是五条等距离的平行线．一条直线交其中的三条平行线于点A，B，C，则 $\frac{A B}{B C} =$ ．

查看试题解析
13. 周末小张和小王去同一个公园跑步，公园有东门、北门两个入口，则他们从同一个入口进入公园的概率是．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ C = 50 °$ ，将 $△ A B C$ 绕点A逆时针旋转到 $△ A B^{'} C^{'}$ ，当点 $B^{'}$ 落在边 $B C$ 上时， $A C^{'} ∥ B C$ ，则 $∠ B =$ ．

查看试题解析
15. 已知点 $A (a ， b)$ 在一次函数 $y = 2 x - 1$ 图象上，则 $a^{2} + b + 3$ 的最小值为．

查看试题解析
16. 已知 $R t △ A B C$ 中， $∠ B = 90 °$ ， $∠ A = 30 ° ， B C = 1 ，$ 含 $30 °$ 角的 $R t △ D E F$ 三个顶点分在 $R t △ A B C$ 的三边上，且直角顶点D在斜边 $A C$ 上，则 $C D$ 的长为．

查看试题解析

三、解答题

17. 计算： $| - 2 | - (\sqrt{3} - 2)^{0} + 4 s i n 30 °$

查看试题解析
18. 解方程组 ${\begin{array}{l} 2 x - y = 4 \\ x + y = 2 \end{array}$

查看试题解析
19. 如图，在平面直角坐标系内，小正方形网格的边长为1个单位长度， $△ A B C$ 的顶点均在格点上．

（ 1 ）作出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ；

（ 2 ）将 $△ D E F$ 向左平移3个单位长度得到 $△ D_{1} E_{1} F_{1}$ ，画出 $△ D_{1} E_{1} F_{1}$ ．

查看试题解析
20. 如图1是一种可折叠的台灯，图2是台灯的结构图， $A C$ 是可以绕点A旋转的支架， $A B$ 是可以绕点B旋转的支架，C为灯泡的位置．量得 $A B = 10 c m ， A C = 20 c m$ ，当 $A B ⊥ B F$ ， $∠ C A B = 127 °$ 时，求点C到 $B F$ 的距离．（参考数据， $s i n 37 ° \approx 0.6$ ， $c o s 37 ° \approx 0.8$ ， $t a n 37 ° \approx 0.75$ ）

查看试题解析
21. 黄岩翻簧竹雕，亦称“贴黄”、“反簧”，是台州地方传统雕刻之一．为了了解学生对于该工艺的熟悉程度，某校设置了丰常了解、了解、了解很少、不了解四个选项，随机抽查了部分学生进行问卷调查，要求每名学生只选其中的一项，并将抽查结果绘制成如下不完整的统计图．

(1)、本次抽样调查的样本容量是；

(2)、补全条形统计图，求扇形统计图中“了解”部分的圆心角度数；

(3)、全校共有1500名学生，请你估计全校学生中“非常了解”和“了解”翻簧竹雕的学生共有多少人．

查看试题解析
22. 如图，在正方形 $A B C D$ 中，对角线 $A C ， B D$ 相交于点O， $∠ D B C$ 的平分线 $B E$ 交 $C D$ 于点E，交 $A C$ 于点F．

(1)、求证： $E C = F C$ ；

(2)、若 $D E = 2$ ，求 $A B$ 的长．

查看试题解析
23. 为了有效地应对高楼火灾，某消防中队进行消防技能比赛．如图，在一个废弃高楼距地面 $10 m$ 的点A和 $15 m$ 的点B处，各设置了一个火源，消防员来到火源正前方，水枪喷出的水流看作抛物线的一部分（水流出口与地面的距离忽略不计）．第一次灭火时站在水平地面的点C处，水流恰好到达点A处，且水流的最大高度为 $16 m$ ，水流的最高点到高楼的水平距离为 $4 m$ ，建立如图所示的平面直角坐标系，水流的高度y（m）与到高楼的水平距离x（m）之间的函数关系式为： $y = a {(x - h)}^{2} + k$ ．

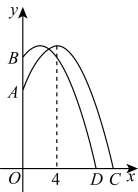(1)、求消防员第一次灭火时水流所在抛物线的解析式；

(2)、待A处火熄灭后，消防员前进2m到点D处进行第二次灭火，若两次灭火时水流所在抛物线的形状相同，请判断水流是否到达点B处，并说明理由；

(3)、若消防员站在到高楼的水平距离为11m~12m的地方，调整水枪，使喷出的水流形状发生变化，水流的最高点到高楼的水平距高始终是4m，当 $- \frac{1}{2} \leq a \leq - \frac{1}{3}$ 时，求水流到达墙面高度的取值范围．

查看试题解析
24. 如图1，已知 $△ A B C$ 内接于 $⊙ O$ ， $A B$ 为 $⊙ O$ 的直径， $A B = 5$ ， $t a n ∠ A B C = \frac{3}{4}$ ，点D是半圆上的一个动点，过点D作 $D E ∥ A C$ 交直径 $A B$ 于点E．

(1)、求证： $∠ A D E = ∠ C B D$ ；

(2)、如图2，连接 $C D$ 交 $A B$ 于点F，若 $∠ A D C = ∠ E D B$ ，求 $c o s ∠ C B D$ ；

(3)、如图3，连接 $C D$ 交 $A B$ 于点F，若 $C D = 2 A E$ ，
①求 $A D$ 的长；

②直接写出 $\frac{B F}{A F}$ 的值为 ▲ ．

查看试题解析

株数（株）	$7$	$12$	$23$	$8$
叶状茎长度（cm）	$45.6$	$46.5$	$46.9$	$47.8$