浙江省宁波市慈溪市2023年中考一模数学试题

试卷更新日期：2023-05-12 类型：中考模拟

进入出卷网下载

一、单选题

1. 3的相反数是（）

A、3 B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、－3

查看试题解析
2. 下列计算正确的是（）

A、 $3^{3} + 3 = 3^{4}$ B、 $3^{3} \cdot 3 = 3^{4}$ C、 $3^{6} \div 3^{2} = 3^{3}$ D、 ${(3^{2})}^{3} = 3^{5}$

查看试题解析
3. “书藏古今，港通天下”是宁波市的城市口号，其中“书藏古今”指的是天一阁，据查，天一阁现藏各类古籍近30万卷，其中数“30万”用科学记数法表示正确的是（）

A、 $30 \times 1 0^{4}$ B、 $3.0 \times 1 0^{4}$ C、 $3.0 \times 1 0^{5}$ D、 $0.30 \times 1 0^{6}$

查看试题解析
4. 如图所示的几何体是由5个相同的小正方体组成的立体图形，则下列四个图形中是它的左视图的是（）

A、 B、 C、 D、

查看试题解析
5. 一个不透明的袋子里装有2个红球和4个白球，它们除颜色外其余都相同，从袋中任意摸出一个球是白球的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{6}$

查看试题解析
6. 已知圆锥的底面周长为 $3 c m$ ，母线长为 $6 c m$ ，则圆锥的侧面积是（）

A、 $9 π c m^{2}$ B、 $9 c m^{2}$ C、 $18 π c m^{2}$ D、 $18 c m^{2}$

查看试题解析
7. 若一组数据1，2，3，x，5，6的众数为5，则这组数据的中位数为（）

A、3 B、3.5 C、4 D、5

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，点D为边 $A B$ 的中点，点E在线段 $A D$ 上， $C E = C D$ ， $E F ⊥ A C$ 于点F，若 $∠ A = 50 °$ ， $A B = 12$ ，则线段 $C F$ 的长为（）

A、3 B、 $3 \sqrt{2}$ C、 $3 \sqrt{3}$ D、4

查看试题解析
9. 在平面直角坐标系中，设二次函数 $y_{1} = x^{2} + 2 b x + a$ ， $y_{2} = a x^{2} + 2 b x + 1$ （a，b；是实数， $a \neq 0$ ）的最小值分别为m和n，若 $m + n = 0$ ，则 $m n$ 的值为（）

A、0 B、 $- 1$ C、 $- 2$ D、 $- 4$

查看试题解析
10. 如图，在正 $△ A B C$ 中，D，E分别在边 $A C$ ， $B C$ 上，连接 $D E$ ， $∠ A D E$ 的平分线过 $△ A B C$ 的内心O，交 $A B$ 于点F，连接 $E F$ ．若要知道 $△ A B C$ 的周长，则只需要知道下列哪个三角形的周长？该三角形是（）

A、 $△ C D E$ B、 $△ A D F$ C、 $△ B E F$ D、 $△ D E F$

查看试题解析

二、填空题

11. 在-1，-2，1，0这四个数中，最小的数是．

查看试题解析
12. 分解因式： $4 - 4 x + x^{2} =$ ．

查看试题解析
13. 对于实数 $x ， y (x \neq y)$ ，我们定义运算 $F (x ， y) = \frac{x + y}{x - y}$ ，如： $F (2 ， 1) = \frac{2 + 1}{2 - 1} = 3$ ．则方程 $F (x ， 1) = 2$ 的解为．

查看试题解析
14. 方程术是中国传统数学著作《九章算术》中最高的代数成就．《九章算术》中记载了这样一个问题：“今有善行者行一百步，不善行者行六十步，今不善行者先行一百步，善行者追之，问几何步及之？”译文：“相同时间内，走路快的人走100步，走路慢的人只走60步，若走路慢的人先走100步，走路快的人要走多少步才能追上？（注：步为长度单位）”，根据题意可求得走路快的人要走步才能追上走路慢的人．

查看试题解析
15. 如图，在 $▱ O A B C$ 中，以O为圆心， $O C$ 为半径的圆切 $A B$ 于点B，F是圆上一动点，作直线 $A F$ 交 $⊙ O$ 于另一点E，当 $E F = B C$ 时， $∠ B A F$ 的度数为．

查看试题解析
16. 如图，在平面直角坐标系中，反比例函数 $y = \frac{k}{x}$ （k为常数， $k \neq 0$ ）的图像经过 $▱ A B C D$ 的顶点B， $A B$ 交y轴于点E， $A B ∥ x$ 轴，F为 $C D$ 边上一点， $A E ： C F ： D F = 1 ： 2 ： 3$ ，连结 $F A$ 并延长交x轴于点G，连结 $D G$ ．

(1)、设 $△ A D F$ 的面积 $S_{1}$ ，四边形 $A B C F$ 的面积为 $S_{2}$ ，则 $S_{1} ： S_{2}$ 的值为，

(2)、当 $△ A D G$ 的面积为3时，k的值为；

查看试题解析

三、解答题

17. 计算：

(1)、计算： ${(x - 1)}^{2} + x (2 - x)$ ；

(2)、解不等式组： ${\begin{array}{l} - 4 x - 3 > 9 \\ - 2 + x \leq 0 \end{array}$ ．

查看试题解析
18. 图1，图2都是由边长为1的正方形构成的网格，每个小正方形的顶点称为格点，线段 $A B$ 的端点均在格点上，分别按要求画出图形．

(1)、在图1中画出等腰直角三角形 $A B C$ ，点C在格点上．

(2)、在图2中画出以 $A B$ 为边的菱形 $A B D E$ ，点D，E在格点上．

查看试题解析
19. 如图，在平面直角坐标系中，抛物线 $y = x^{2} - a x$ 经过点 $(5 ， 5)$ ，顶点为A，连结 $O A$ ．

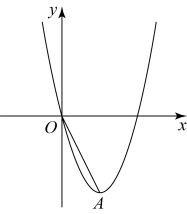(1)、求a的值．

(2)、求A的坐标．

(3)、P为x轴上的动点，当 $t a n ∠ O P A = \frac{1}{2}$ 时，请直接写出OP的长．

查看试题解析
20. “双减”政策实施后，为丰富学生的学习生活，某校数学组增设拓展课，计划成立“思维挑战”、“神奇幻方”、“智力谜题”、“画板几何”和“数学家们”五个拓展课，为了了解学生报名意向，随机抽查了部分学生进行调查问卷，要求每位学生选择其中一个课程，并将结果绘制成如下不完整的统计图．

根据统计图中的信息，解答下列问题：

(1)、求本次被抽查学生的总人数．

(2)、求扇形统计图中表示“智力谜题”的扇形的圆心角度数．

(3)、若该校共有990名学生，根据抽查结果，试估计全校选择“思维挑战”拓展课的学生人数．

查看试题解析
21. 如图是某风车平面示意图，其相同的四个叶片均匀分布，水平地面上的点M在旋转中心O的正下方．某一时刻，太阳光线恰好垂直照射叶片 $O A ， O B$ ，此时各叶片影子在点M右侧形成线段 $C E$ ， O的对应点为D，测得 $M C = 4 m ， C E = 16 m$ ，此时太阳的与地面的夹角为 $30 °$ （即 $∠ O D M = 30 °$ ）．

(1)、求旋转中心到地面的距离 $O M$ 的值．

(2)、风车转动时，要求叶片外端离地面的最低高度高于 $2.5$ 米，请判断此风车是否符合要求．

查看试题解析
22. 有一块形状如图1的四边形余料 $A B C D$ ， $A B = 6$ ， $A D = 2$ ， $∠ A = 90 °$ ， $∠ D = 135 °$ ， $t a n ∠ B = 2$ ，要在这块余料上截取一块矩形材料，其中一条边在 $A B$ 上．

(1)、如图2，若所截矩形材料的另一条边 $A E$ 在 $A D$ 上，设 $A E = x$ ，矩形 $A E F G$ 的面积为y，
①求y关于x的函数表达式．

②求矩形面积y的最大值．

(2)、能否截出比（1）中更大面积的矩形材料？如果能，求出这些矩形材料面积的最大值；如果不能，说明理由．

查看试题解析
23.

(1)、[证明体验]如图1，在 $△ A B C$ 中，D为 $A B$ 边上一点，连接 $C D$ ，若 $∠ A C D = ∠ A B C$ ，求证： $A C^{2} = A D \cdot A B$ ．

(2)、在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， ∠ A B C = 60 °$ ， $B C = 2$ ， D为 $A B$ 边上一动点，连接 $C D$ ， E为 $C D$ 中点，连接 $B E$ ．
①[思考探究]如图2，当 $∠ A C D = ∠ D B E$ 时，求 $A D$ 的长．

②[拓展延伸]如图3，当 $∠ D E B = 30 °$ 时，求 $A D$ 的长．

查看试题解析
24. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $A B = A D$ ， $A C$ 为直径，E为 $\overset{⌢}{A D}$ 上一动点，连接 $B E$ 交 $A C$ 于点G，交 $A D$ 于点F，连接 $D E$ ．

(1)、设∠E为 $α$ ，请用 $α$ 表示 $∠ B A C$ 的度数．

(2)、如图1，当 $B E ⊥ A D$ 时，
①求证： $D E = B G$ ．
②当 $t a n ∠ A B E = \frac{3}{4}$ ， $B G = 5$ 时，求半径的长．

(3)、如图2，当 $B E$ 过圆心O时，设 $t a n ∠ A B E = x$ ， $\frac{B F}{E F} = y$ ，求y关于x的函数表达式．

查看试题解析