四川省成都市锦江区2023年中考二模训练数学试题
试卷更新日期:2023-05-12 类型:中考模拟
一、单选题
-
1. 36的算术平方根是( )
A、±6 B、6 C、± D、2. 一个几何体如图水平放置,它的俯视图是( )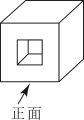 A、
A、 B、
B、 C、
C、 D、
D、 3. 清代诗人袁枚创作了一首诗《苔》:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”歌颂了苔在恶劣环境下仍有自己的生命意向.若苔花的花粉粒直径线约为0.0000084米,用科学记数法表示 , 则n为( )A、 B、5 C、 D、64. 已知点A(4,3)和点B是坐标平面内的两个点,且它们关于直线x=﹣3对称,则平面内点B的坐标为( )A、(0,﹣3) B、(4,﹣9) C、(4,0) D、(﹣10,3)5. 某中学随机抽取了该校53名学生,他们的年龄如表所示:这53名学生年龄的众数和中位数分别是( )
3. 清代诗人袁枚创作了一首诗《苔》:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”歌颂了苔在恶劣环境下仍有自己的生命意向.若苔花的花粉粒直径线约为0.0000084米,用科学记数法表示 , 则n为( )A、 B、5 C、 D、64. 已知点A(4,3)和点B是坐标平面内的两个点,且它们关于直线x=﹣3对称,则平面内点B的坐标为( )A、(0,﹣3) B、(4,﹣9) C、(4,0) D、(﹣10,3)5. 某中学随机抽取了该校53名学生,他们的年龄如表所示:这53名学生年龄的众数和中位数分别是( )年龄(单位:岁)
12
13
14
15
人数
12
14
18
9
A、13岁、14岁 B、14岁,14岁 C、14岁,13岁 D、14岁,15岁6. 《九章算术》是中国古代的一本重要数学著作,其中有一道方程的应用题:“五只雀、六只燕,共重16两,雀重燕轻.互换其中一只,恰好一样重.问每只雀、燕的重量各为多少?”解:设雀每只x两,燕每只y两,则可列出方程组为( )A、 B、 C、 D、7. 如图,正六边形和正方形都内接于 , 连接 , 则弦所对圆周角的度数为( ) A、 B、 C、或 D、或8. 如图,二次函数的图象与轴交于 , 两点,与轴负半轴交于点 , 它的对称轴为直线 , 则下列选项中正确的是( )
A、 B、 C、或 D、或8. 如图,二次函数的图象与轴交于 , 两点,与轴负半轴交于点 , 它的对称轴为直线 , 则下列选项中正确的是( )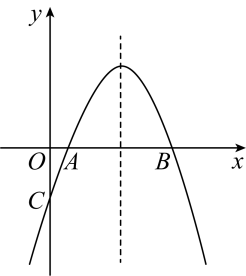 A、 B、 C、 D、当(为实数)时,
A、 B、 C、 D、当(为实数)时,二、填空题
-
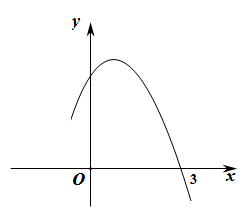
9. 因式分解: .10. 当x=时,分式 与分式 的值互为相反数.11. 二次函数y=ax2-2ax-m的部分图象如图所示,则方程ax2-2ax-m=0的根 .
 12. 如图,高为6m的电线杆的顶上有一盏路灯,电线杆底部为A,身高1.5m的男孩站在与点A相距6m的点B处,若男孩以6m为半径绕电线杆走一圈,则他在路灯下的影子BC=m;BC扫过的面积为m2 .
12. 如图,高为6m的电线杆的顶上有一盏路灯,电线杆底部为A,身高1.5m的男孩站在与点A相距6m的点B处,若男孩以6m为半径绕电线杆走一圈,则他在路灯下的影子BC=m;BC扫过的面积为m2 .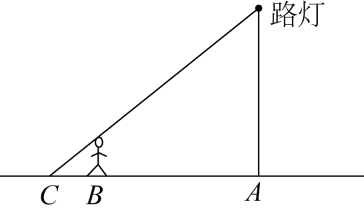 13. 如图,在中, , 分别以点A、C为圆心,大于长为半径画弧,两弧分别相交于点M、N,直线与相交于点E,过点C作 , 垂足为点D,与相交于点F,若 , 则的度数为 .
13. 如图,在中, , 分别以点A、C为圆心,大于长为半径画弧,两弧分别相交于点M、N,直线与相交于点E,过点C作 , 垂足为点D,与相交于点F,若 , 则的度数为 .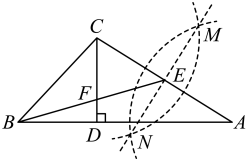
三、解答题
-
14.(1)、计算: .(2)、解不等式组:15. 我市为加快推进生活垃圾分类工作,对分类垃圾桶实行统一的外型、型号、颜色等,其中,可回收物用蓝色收集桶,有害垃圾用红色收集桶,厨余垃圾用绿色收集桶,其他垃圾用灰色收集桶.为了解学生对垃圾分类知识的掌握情况,某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生,根据调查结果,绘制了如图所示的两幅不完整的统计图.
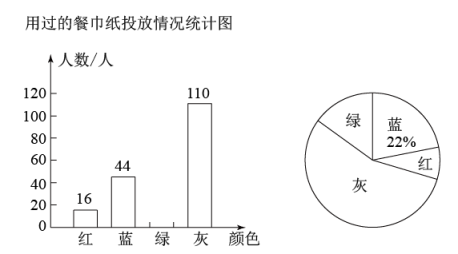
根据图中信息,解答下列问题:
(1)、此次调查一共随机采访了名学生,在扇形统计图中,“灰”所在扇形的圆心角的度数为度;(2)、若该校有3600名学生,估计该校学生将用过的餐巾纸投放到红色收集桶的人数;(3)、李老师计划从A,B,C,D四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛,请用树状图法或列表法求出恰好抽中A,B两人的概率.16. 如图,修筑铁路时需打通小山修一条隧道.测绘时用一架无人机沿直线l飞行,飞行高度为1200米,在A处测得隧道一端M处的俯角为37°,飞行2800米后到达B处测得隧道另一端N处的俯角为76°,已知A,B,M,N四点在同一平面内,且 , 求隧道的长.(参考数据: , , , ) 17. 如图,已知AB是⊙O的直径,点E是⊙O上异于A,B的点,点F是的中点,连接AE,AF,BF,过点F作FC⊥AE交AE的延长线于点C,交AB的延长线于点D,∠ADC的平分线DG交AF于点G,交FB于点H.
17. 如图,已知AB是⊙O的直径,点E是⊙O上异于A,B的点,点F是的中点,连接AE,AF,BF,过点F作FC⊥AE交AE的延长线于点C,交AB的延长线于点D,∠ADC的平分线DG交AF于点G,交FB于点H. (1)、求证:CD是⊙O的切线;(2)、求sin∠FHG的值;(3)、若GH= , HB=2,求⊙O的直径.18. 如图1,平面直角坐标系中, , 反比例函数的图象分别交矩形的两边、于E、F(E、F不与A重合),沿着将矩形折叠使A、D重合.
(1)、求证:CD是⊙O的切线;(2)、求sin∠FHG的值;(3)、若GH= , HB=2,求⊙O的直径.18. 如图1,平面直角坐标系中, , 反比例函数的图象分别交矩形的两边、于E、F(E、F不与A重合),沿着将矩形折叠使A、D重合.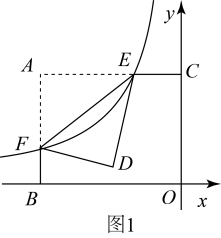
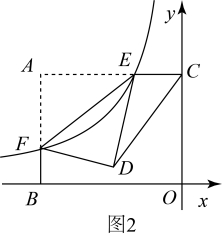
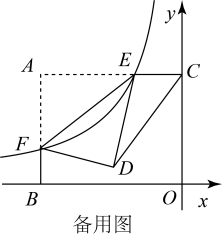 (1)、当点E为中点时,求点F的坐标,并直接写出与对角线的关系;(2)、如图2,连接 .
(1)、当点E为中点时,求点F的坐标,并直接写出与对角线的关系;(2)、如图2,连接 .①的周长是否有最小值,若有,请求出最小值;若没有,请说明理由;
②当平分时,直接写出k的值.
四、填空题
-
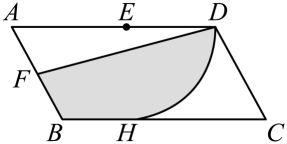
19. 已知m,n是方程 的两个根,则代数式 的值是 .20. 已知二次函数 , 当时,该函数取最大值12.设该函数图象与x轴的一个交点的横坐标为 , 若 , 则a的取值范围是 .21. 如图,在平行四边形ABCD中,AD=8,AB=4,∠BAD=60°,E为AD上一点,以点E为圆心,以ED的长为半径作弧与BC相切于点H,点F为线段AB中点,则阴影部分面积为 .
 22. 直线y=-x+2a(常数)和双曲线的图象有且只有一个交点B,一次函数y=-x+2a与x轴交于点A,点P是线段OA上的动点,点Q在反比例函数图象上,且满足∠BPO=∠QPA.设PQ与线段AB的交点为M,若OM⊥BP,则的值为 .
22. 直线y=-x+2a(常数)和双曲线的图象有且只有一个交点B,一次函数y=-x+2a与x轴交于点A,点P是线段OA上的动点,点Q在反比例函数图象上,且满足∠BPO=∠QPA.设PQ与线段AB的交点为M,若OM⊥BP,则的值为 . 23. 在数学“折向未来”的活动课上,小明用如图所示的长方形纸片折四边形, , 点E,G分别是边上的中点,点F,H分别是边上的点,且 , 连接 . 将 , 分别沿 , 翻折,点B的对应点为点 , 点D的对应点为点 , 当点落在线段上时,则cm;当点在内部时,连接 , 若为直角三角形,则四边形的面积为 .
23. 在数学“折向未来”的活动课上,小明用如图所示的长方形纸片折四边形, , 点E,G分别是边上的中点,点F,H分别是边上的点,且 , 连接 . 将 , 分别沿 , 翻折,点B的对应点为点 , 点D的对应点为点 , 当点落在线段上时,则cm;当点在内部时,连接 , 若为直角三角形,则四边形的面积为 .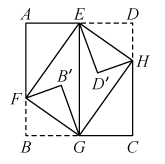
五、解答题
-
24. 金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:
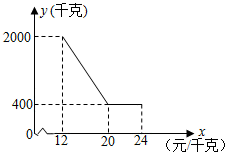 (1)、求y与x之间的函数解析式;(2)、求这一天销售羊肚菌获得的利润W的最大值;(3)、若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.25. 如图,在平面直角坐标系中,抛物线交x轴于点A、B,交y轴于点C.
(1)、求y与x之间的函数解析式;(2)、求这一天销售羊肚菌获得的利润W的最大值;(3)、若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.25. 如图,在平面直角坐标系中,抛物线交x轴于点A、B,交y轴于点C.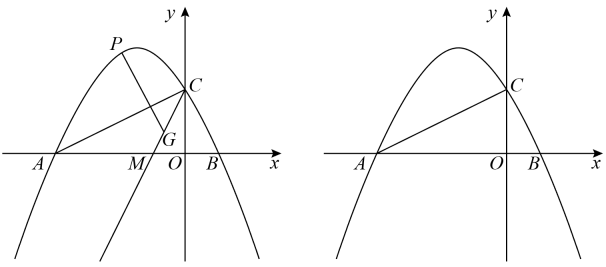 (1)、求△ABC的面积;(2)、如图,过点C作射线CM,交x轴的负半轴于点M,且∠OCM=∠OAC,点P为线段AC上方抛物线上的一点,过点P作AC的垂线交CM于点G,求线段PG的最大值及点P的坐标;(3)、将该抛物线沿射线AC方向平移个单位后得到的新抛物线为 , 新抛物线与原抛物线的交点为E,点F为新抛物线y对称轴上的一点,在平面直角坐标系中是否存在点Q,使以点A、E、F、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.26. 如图.已知为等腰直角三角形, , D、E分别为上的两点, , 连接 , 将绕点E逆时针旋转得 , 连接与交于点M.
(1)、求△ABC的面积;(2)、如图,过点C作射线CM,交x轴的负半轴于点M,且∠OCM=∠OAC,点P为线段AC上方抛物线上的一点,过点P作AC的垂线交CM于点G,求线段PG的最大值及点P的坐标;(3)、将该抛物线沿射线AC方向平移个单位后得到的新抛物线为 , 新抛物线与原抛物线的交点为E,点F为新抛物线y对称轴上的一点,在平面直角坐标系中是否存在点Q,使以点A、E、F、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.26. 如图.已知为等腰直角三角形, , D、E分别为上的两点, , 连接 , 将绕点E逆时针旋转得 , 连接与交于点M.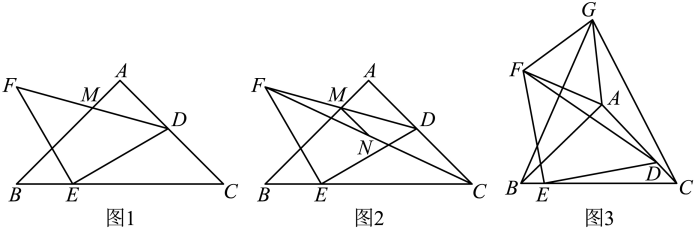 (1)、如图1,当时,若 , 求的长;(2)、如图2,连接 , 为的中点,连接 , 求证:;(3)、如图3,连接 , 将绕点A顺时针旋转得 , 连接、、 , 若 , 当周长取得最小值时,直接写出的面积.
(1)、如图1,当时,若 , 求的长;(2)、如图2,连接 , 为的中点,连接 , 求证:;(3)、如图3,连接 , 将绕点A顺时针旋转得 , 连接、、 , 若 , 当周长取得最小值时,直接写出的面积.