广西贺州市2023年中考一模数学试题

试卷更新日期：2023-05-12 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，数轴上点Q所表示的数可能是（）

A、 $1.5$ B、 $2.6$ C、 $- 0.7$ D、 $0.4$

查看试题解析
2. 围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史.下列由黑白棋子摆成的图案是轴对称图形的是（）

A、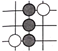 B、 C、 D、

查看试题解析
3. 水中涟漪（圆形水波）不断扩大，记它的半径为r，则圆周长C与r的关系式为 $C = 2 π r$ ．下列判断正确的是（）

A、2是变量 B、 $π$ 是变量 C、r是变量 D、C是常量

查看试题解析
4. 点 $(4 ， - 3)$ 往右平移一个单位长度后坐标为（）

A、 $(5 ， - 3)$ B、 $(3 ， - 3)$ C、 $(4 ， - 2)$ D、 $(4 ， - 4)$

查看试题解析
5.
如图是一块带有圆形空洞和方形空洞的小木板，则下列物体中既可以堵住圆形空洞，又可以堵住方形空洞的是( )

A、 B、 C、 D、

查看试题解析
6. 若 $⊙ O$ 的半径为3，圆心 $O$ 到直线l的距离为3，那么直线与 $⊙ O$ 的位置关系是（）

A、相离 B、相切 C、相交 D、不能确定

查看试题解析
7. 如图，直线 $a ∥ b$ ，将含 $30 °$ 角的直角三角板的直角顶点放在直线b上，已知 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、 $55 °$ B、 $60 °$ C、 $65 °$ D、 $70 °$

查看试题解析
8. 下列运算正确的是（）

A、3a²+4a²=7a⁴ B、3a²-4a²=-a² C、3a•4a²=12a² D、 ${(3 a^{2})}^{2} \div 4 a^{2} = \frac{3}{4} a^{2}$

查看试题解析
9. 假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．如果3枚鸟卵全部成功孵化，那么3只雏鸟中恰有2只雄鸟的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{8}$ D、 $\frac{2}{3}$

查看试题解析
10. 如图，一次函数 $y = \frac{3}{2} x$ 的图象与 $y = k x + 7$ 的图象相交于点A，则方程组 ${\begin{array}{l} y = k x + 7 \\ y = \frac{3}{2} x \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ B、 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 3 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$

查看试题解析
11. 如图，某校生物兴趣小组用长为18米的篱笆，一面利用墙（墙的最大可用长度为11米），围成中间隔有一道篱笆的长方形花圃 $A B C D$ ，为了方便出入，建造篱笆花圃时在 $B C$ 边留了宽为1米的两个进出口（不需材料），若花圃的面积刚好为40平方米，设 $A B$ 的长为x米，则可列方程为（）

A、 $x (18 - 3 x) = 40$ B、 $x (20 - 2 x) = 40$ C、 $x (22 - 3 x) = 40$ D、 $x (20 - 3 x) = 40$

查看试题解析
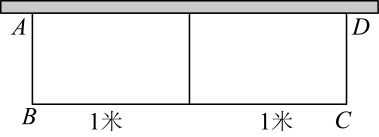12. 将边长为3的等边三角形 $A B C$ 和另一个边长为1的等边三角形 $D E F$ 如图放置（EF在 $A B$ 边上，且点E与点B重合）．第一次将 $△ D E F$ 以点F为中心旋转至 $△ E_{1} F D_{1}$ ，第二次将 $△ E_{1} F D_{1}$ 以点 $D_{1}$ 为中心旋转至 $△ F_{1} D_{1} E_{2}$ 的位置，第三次将 $△ F_{1} D_{1} E_{2}$ 以点 $E_{2}$ 为中心旋转至 $△ D_{2} E_{2} F_{2}$ 的位置，…，按照上述办法旋转，直到 $△ D E F$ 再次回到初始位置时停止，在此过程中 $△ D E F$ 的内心O点运动轨迹的长度是（）

A、 $\frac{4}{3} π$ B、 $\frac{8}{3} π$ C、 $\frac{4 \sqrt{3}}{3} π$ D、 $\frac{8 \sqrt{3}}{3} π$

查看试题解析

二、填空题

13. 当x时， $\sqrt{x - 1}$ 有意义．

查看试题解析
14. 因式分解： $x^{2} - 4 =$ .

查看试题解析
15. 若x₁ ， x₂是方程x²-3x+2＝0的两个根，则x₁•x₂＝．

查看试题解析
16. 比较大小： $40.15 °$ $40 ° 1 5^{'}$ （用 $>$ 、 $=$ 、 $<$ 填空）．

查看试题解析
17. 某校男子足球队的年龄分布如图所示，则这些队员年龄的众数是岁．

查看试题解析
18. 如图，已知直线 $y = \frac{1}{2} x$ 与双曲线 $y = \frac{8}{x}$ 交于A，B两点，过原点O的另一条直线l交双曲线于P，Q两点（点P在第一象限），若由点A，B，P，Q为顶点的四边形面积为24，则点P的坐标为．

查看试题解析

三、解答题

19. 计算： $- 1^{2023} + 8 \div (- 2)^{2} - | - 4 | \times 5$ ．

查看试题解析
20. 化简求值： $(\frac{2 a}{a + 1} - 1) \div \frac{{(a - 1)}^{2}}{a + 1}$ ，其中 $a = 3$ ．

查看试题解析
21. 如图， $△ A B C$ 是⊙O的内接三角形，且 $A B$ 为直径．

(1)、请用尺规作 $∠ C$ 的平分线，交 $⊙ O$ 于点D；（不要求写作法，但需要保留作图痕迹）

(2)、连接 $A D$ ， $B D$ ，若 $A C = 6 ， B C = 8$ ，求线段 $A D$ 的长．

查看试题解析
22. 为了了解养殖鱼的生长情况，养鱼者从鱼塘中捕捞了20条鱼，称得它们的质量如下：
质量（kg）
1.0
1.2
1.5
1.8
频数（条）
4
5
8
3

(1)、请直接写出样本的中位数；

(2)、请计算样本平均数，并根据计算结果估计鱼塘这种鱼的平均质量；

(3)、若养鱼者对打捞的每一条鱼身上做好记号后把这些鱼放归鱼塘，过了一段时间（该时间间隔对鱼的质量变化忽略不计），再从中打捞了100条鱼，其中有2条鱼是有记号的，请你估计该鱼塘鱼的总质量．

查看试题解析
23. 综合与实践
【问题情境】南宁青秀山龙象塔始建于明代万历年间，塔呈八角形，九级重檐结构，是青秀山的地标建筑．在一次数学综合实践活动中，李老师布置了一个任务：请根据所学知识设计一种方案，测量龙象塔的高．

(1)、【实践探究】某小组通过思考，绘制了如图2所示的测量示意图，即在水平地面上的点C处测得塔顶端A的仰角为 $α$ ，点C到点B的距离 $B C = a$ 米，即可得出塔高 $A B =$ 米（请你用所给数据 $α$ 和a表示）．

(2)、【问题解决】但在实践中发现：由于无法直接到达塔底端的B点，因此BC无法直接测量．该小组对测量方案进行了如下修改：如图3，从水平地面的C点向前走a米到达点D处后，在D处测得塔顶端A的仰角为 $β$ ，即可通过计算求得塔高AB．若测得的 $α = 45 °$ ， $β = 60 °$ ， $C D = 22$ 米，请你利用所测数据计算塔高AB．（计算结果精确到1米，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
24. 广西“钦蜜九号”黄金百香果以“味甜浓香”深受广大顾客的喜爱，某超市用3600元购进一批黄金百香果，很快就销售一空；超市又用5400元购进了第二批黄金百香果，此时大量水果上市，所购买的重量是第一批的2倍，但是每千克黄金百香果比第一批便宜了5元．

(1)、该超市购进第一批和第二批黄金百香果每千克的单价分别是多少元？

(2)、如果这两批黄金百香果都以相同的标价出售，要使两批黄金百香果全部售完后的利润率不低于50%（不计其他因素），则超市应该将黄金百香果至少标价每千克多少元出售？

查看试题解析
25. 如图，在矩形 $A B C D$ 的 $B C$ 边上取一点E，将 $△ A B E$ 沿直线 $A E$ 折叠得到 $△ A F E$ ，此时点B的对称点F恰好落在边 $C D$ 上，G为 $A D$ 中点，连接BG分别与 $A E$ ， $A F$ 交于M，N两点，且 $∠ B E M = ∠ B M E$ ，连接 $F M$ ．

(1)、求证：四边形 $B E F M$ 为菱形；

(2)、猜想 $C E$ 和 $M N$ 的数量关系，并说明理由；

(3)、 $A D = 4$ ，求线段 $C E$ 的长和 $s i n ∠ D A F$ 的值．

查看试题解析
26. 如图1，抛物线 $y = - x^{2} + 2 x + 3$ 与 $x$ 轴交于A，B两点（点A在左侧），与y轴交于点C，点P为直线 $B C$ 上方抛物线上的一个动点，过点P作 $P D ∥ y$ 轴交直线 $B C$ 于点D，

(1)、求点A，B，C的坐标；

(2)、设点P的横坐标为m，请用含m的式子表示线段 $P D$ 的长；

(3)、如图2，连接 $O P$ ，交线段 $B C$ 于点Q，连接PC，若 $△ P C Q$ 的面积为 $S_{1}$ ， $△ O C Q$ 的面积为 $S_{2}$ ，则 $\frac{S_{1}}{S_{2}}$ 是否有最大值？如果有，请求出最大值；如果没有，请说明理由．

查看试题解析

质量（kg）	1.0	1.2	1.5	1.8
频数（条）	4	5	8	3