2022-2023学年人教版八年级期末复习 勾股定理
试卷更新日期:2023-05-12 类型:复习试卷
一、单选题
-
1. 如图,将矩形ABCD沿直线DE折叠,顶点A落在BC边上F处,已知 , , 则BF的长为( )
 A、5 B、4 C、3 D、22. 在 中, , , 的平分线交 于点 ,若 ,则 长为( )A、 B、6 C、 D、83. 如图所示的一段楼梯,高BC是3米,斜边AB长是5米,现打算在楼梯上铺地毯,至少需要地毯的长度为( )
A、5 B、4 C、3 D、22. 在 中, , , 的平分线交 于点 ,若 ,则 长为( )A、 B、6 C、 D、83. 如图所示的一段楼梯,高BC是3米,斜边AB长是5米,现打算在楼梯上铺地毯,至少需要地毯的长度为( ) A、5米 B、6米 C、7米 D、8米4. 若一个直角三角形的两边长为12和5,则第三边为 ( )A、13 B、13或 C、13或5 D、155. 下列所给的各组线段,能组成直角三角形的是:( )A、3cm、4cm、5cm B、2cm、3cm、5cm C、2cm、3cm、6cm D、3cm、5cm、6cm6. 如图,在矩形 中, , ,将矩形沿 折叠,点 落在点 处,则重叠部分 的面积为( )
A、5米 B、6米 C、7米 D、8米4. 若一个直角三角形的两边长为12和5,则第三边为 ( )A、13 B、13或 C、13或5 D、155. 下列所给的各组线段,能组成直角三角形的是:( )A、3cm、4cm、5cm B、2cm、3cm、5cm C、2cm、3cm、6cm D、3cm、5cm、6cm6. 如图,在矩形 中, , ,将矩形沿 折叠,点 落在点 处,则重叠部分 的面积为( ) A、6 B、12 C、10 D、207. 如图,在中, , D、E分别是AB、AC的中点,连结DE、CD。若 , , 则CD的长为( )
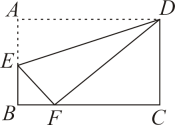
A、6 B、12 C、10 D、207. 如图,在中, , D、E分别是AB、AC的中点,连结DE、CD。若 , , 则CD的长为( )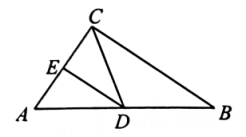 A、7 B、6 C、5 D、4.88. 如图,在 中, , , ,点D在边 上, , ,垂足为点F,交 于点E,则 的长为( )
A、7 B、6 C、5 D、4.88. 如图,在 中, , , ,点D在边 上, , ,垂足为点F,交 于点E,则 的长为( ) A、2 B、 C、 D、9. 如图,在矩形 中, ,点E是边 上一动点,将 沿直线 对折,点A的落点为 ,当 为直角三角形时,线段 的长为( )
A、2 B、 C、 D、9. 如图,在矩形 中, ,点E是边 上一动点,将 沿直线 对折,点A的落点为 ,当 为直角三角形时,线段 的长为( ) A、3 B、4 C、6或3 D、3或410. 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
A、3 B、4 C、6或3 D、3或410. 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )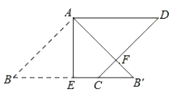 A、1 B、 C、2- D、2 ﹣2
A、1 B、 C、2- D、2 ﹣2二、填空题
-
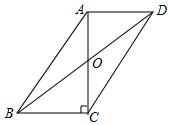
11. 如图,在▱ABCD中,AB=10,AD=6,AC⊥BC,交BD于点O,则BD的长为 .
 12. 公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”如图所示,设勾a=6,弦c= 10,则小正方形ABCD的面积是
12. 公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”如图所示,设勾a=6,弦c= 10,则小正方形ABCD的面积是 13. 如图,已知 , 以为直角边作 , 并使 , 再以为直角边作 , 并使 , 再以为直角边作 , 并使 , …按此规律进行下去,则的直角边的长为 .
13. 如图,已知 , 以为直角边作 , 并使 , 再以为直角边作 , 并使 , 再以为直角边作 , 并使 , …按此规律进行下去,则的直角边的长为 . 14. 如图,在Rt ABC中,∠C=90°,AC=6cm,BC=8cm.将Rt ABC绕点A逆时针旋转得到Rt ,使点C '落在AB边上,连结 ,则 的长度为 .
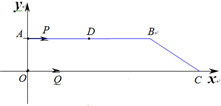
14. 如图,在Rt ABC中,∠C=90°,AC=6cm,BC=8cm.将Rt ABC绕点A逆时针旋转得到Rt ,使点C '落在AB边上,连结 ,则 的长度为 . 15. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .
15. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .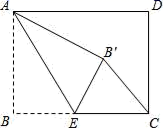
三、解答题
-
16. 如图,已知在 中, 边上的高 求 边的长.
 17. 如图,在中, , , , , 是的中位线.求证:四边形是矩形.
17. 如图,在中, , , , , 是的中位线.求证:四边形是矩形. 18. 如图,有两只猴子在一棵树CD高6m的点B处,他们都要到A处的池塘去喝水,其中一只猴子沿树爬下去到离树12m处的池塘A处,另一只猴子爬到树顶D后直线越向池塘的A处,如果两只猴子所经过的路程相等,这棵树高有多少米?
18. 如图,有两只猴子在一棵树CD高6m的点B处,他们都要到A处的池塘去喝水,其中一只猴子沿树爬下去到离树12m处的池塘A处,另一只猴子爬到树顶D后直线越向池塘的A处,如果两只猴子所经过的路程相等,这棵树高有多少米? 19. 如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
19. 如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积. 20. 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如下图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?
20. 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如下图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少? 21. 已知a,b,c是△ABC的三边长,且满足 ,试判断△ABC的形状。
21. 已知a,b,c是△ABC的三边长,且满足 ,试判断△ABC的形状。
四、综合题