2023年江苏省苏州市中考数学模拟卷
试卷更新日期:2023-05-12 类型:中考模拟
一、单选题(每题3分,共24分)
-
1. 下列四个实数中,最小的实数是( )A、 B、0 C、 D、12. 2020年7月23日,中国首次火星探测任务探测器“天文一号”顺利升空.并于2021年2月到达火星,实施火星捕获.截至2021年2月3日,“天文一号”探测器总飞行里程已超过4.5亿公里.若用科学记数法表示4.5亿,正确的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 某校为了了解学生对《中华人民共和国民法典》的认知情况,在全校1260名学生中,随机抽取部分学生进行调查,把学生的认知情况分为三类:A;完全不知道,B:听过但没读过,C:读过一部分.根据调查结果绘制成如下两幅不完整的统计图,根据图中信息,下列说法错误的是()
 A、此次调查抽取的人数是60人 B、抽取的学生中,“读过一部分”的同学有24人 C、“听过但没读过”所在的扇形的圆心角的度数是 D、估计全校学生中有315人属于“完全不知道”的情况5. 两个矩形的位置如图所示,若 , 则( )
A、此次调查抽取的人数是60人 B、抽取的学生中,“读过一部分”的同学有24人 C、“听过但没读过”所在的扇形的圆心角的度数是 D、估计全校学生中有315人属于“完全不知道”的情况5. 两个矩形的位置如图所示,若 , 则( )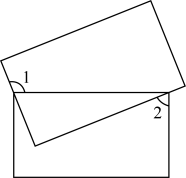 A、 B、 C、 D、6. 如图, 是一块绿化带,将阴影部分修建为花圃.已知 , , ,阴影部分是 的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( ).
A、 B、 C、 D、6. 如图, 是一块绿化带,将阴影部分修建为花圃.已知 , , ,阴影部分是 的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( ).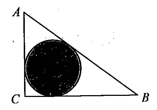 A、 B、 C、 D、7. 我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺?( )A、8尺 B、12尺 C、16尺 D、18尺8. 如图,平行四边形ABCD中,BD=AB,∠ABD=30°,将平行四边形ABCD绕点A旋转至平行四边形AMNE的位置,使点E落在BD上, ME交AB于点O, 则 的值是( )
A、 B、 C、 D、7. 我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺?( )A、8尺 B、12尺 C、16尺 D、18尺8. 如图,平行四边形ABCD中,BD=AB,∠ABD=30°,将平行四边形ABCD绕点A旋转至平行四边形AMNE的位置,使点E落在BD上, ME交AB于点O, 则 的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共24分)
-
9. 计算的结果等于 .10. 已知 , 则.11. 计算的结果是 .12. 在等腰 中, 的对边分别为 ,已知 和 是关于 的方程 的两个实数根,则 的周长是 .13. 如图,BC是 的弦,AD过圆心O,且 .若 ,则 的度数为.
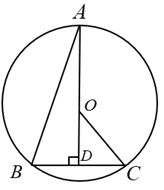 14. 如图,已知是内的一点, , , 若的面积为2, , , 则的面积是.
14. 如图,已知是内的一点, , , 若的面积为2, , , 则的面积是. 15. 在市区内,我市乘坐出租车的价格 (元)与路程 (km)的函数关系图像如图所示.出差归来的小李从火车站乘坐出租车回家用了18元,火车站到小李家的路程为km .
15. 在市区内,我市乘坐出租车的价格 (元)与路程 (km)的函数关系图像如图所示.出差归来的小李从火车站乘坐出租车回家用了18元,火车站到小李家的路程为km .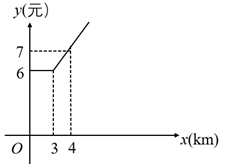 16. 如图,矩形ABCD中, , , 点E是BC的中点,点F在AB上, , P是矩形上一动点.若点P从点F出发,沿的路线运动,当时,FP的长为 .
16. 如图,矩形ABCD中, , , 点E是BC的中点,点F在AB上, , P是矩形上一动点.若点P从点F出发,沿的路线运动,当时,FP的长为 .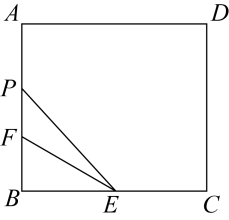
三、解答题(共11题,共82分)
-
17. 计算:18. 解分式方程:+=2.19. 已知 , 求代数式的值.20. 有四张规格、质地相同的卡片,它们背面完全相同,正面图案分别是A 菱形,B 平行四边形,C 线段,D 角,将这四张卡片背面朝上洗匀后(1)、随机抽取一张卡片图案是轴对称图形的概率是;(2)、随机抽取两张卡片(不放回),求两张卡片卡片图案都是中心对称图形的概率,并用树状图或列表法加以说明.21. 如图,四边形 为矩形,G是对角线 的中点.连接 并延长至F,使 ,以 、 为邻边作 ,连接 .
 (1)、若四边形 是菱形,判断四边形 的形状,并证明你的结论.(2)、在(1)条件下,连接 ,若 ,求 的长.22. 每年的4月23日是“世界读书日”,今年4月,某校开展了以“风飘书香满校园”为主题的读书活动,活动结束后,校教务处对本校八年级学生.4月份的读书进行了随机抽样调查,并对所有随机抽取学生的读书量(单位:本)进行了统计,如图所示:根据以上信息,解答下列问题:
(1)、若四边形 是菱形,判断四边形 的形状,并证明你的结论.(2)、在(1)条件下,连接 ,若 ,求 的长.22. 每年的4月23日是“世界读书日”,今年4月,某校开展了以“风飘书香满校园”为主题的读书活动,活动结束后,校教务处对本校八年级学生.4月份的读书进行了随机抽样调查,并对所有随机抽取学生的读书量(单位:本)进行了统计,如图所示:根据以上信息,解答下列问题: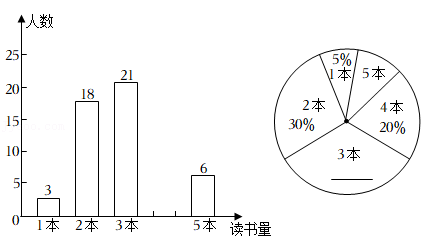 (1)、补全左边的条形统计图,并在右边扇形统计图横线上填空;(2)、本次抽取学生4月份“读书量”的众数为 , 平均数为 本,中位数为 ;(3)、已知该校八年级有700名学生,请你估计该校八年级学生中4月份“读书量”不少于4本的学生人数.23. 在平面直角坐标系 中,直线 与一次函数 的图象交于点 与反比例函数 的图象交于点 ,点 与点 关于 轴对称.(1)、直接写出点 的坐标;(2)、求点 的坐标(用含m的式子表示);(3)、若 两点中只有一个点在线段 上,直接写出 的取值范围.24. 如图,AB是 的直径,AC是弦,D是 的中点,CD与AB交于点E.F是AB延长线上的一点,且 .
(1)、补全左边的条形统计图,并在右边扇形统计图横线上填空;(2)、本次抽取学生4月份“读书量”的众数为 , 平均数为 本,中位数为 ;(3)、已知该校八年级有700名学生,请你估计该校八年级学生中4月份“读书量”不少于4本的学生人数.23. 在平面直角坐标系 中,直线 与一次函数 的图象交于点 与反比例函数 的图象交于点 ,点 与点 关于 轴对称.(1)、直接写出点 的坐标;(2)、求点 的坐标(用含m的式子表示);(3)、若 两点中只有一个点在线段 上,直接写出 的取值范围.24. 如图,AB是 的直径,AC是弦,D是 的中点,CD与AB交于点E.F是AB延长线上的一点,且 .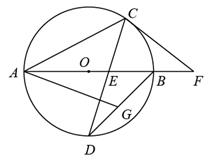 (1)、求证: 为 的切线;(2)、连接BD,取BD的中点G,连接AG.若 , ,求AG的长.25. 昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需要136元;若购买2个大地球仪和1个小地球仪需要132元.(1)、求每个大地球仪和每个小地球仪各多少元;(2)、昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪.26. 如图,在平面直角坐标系中,抛物线 , y与 轴交于A、B两点,与 轴交于点C.
(1)、求证: 为 的切线;(2)、连接BD,取BD的中点G,连接AG.若 , ,求AG的长.25. 昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需要136元;若购买2个大地球仪和1个小地球仪需要132元.(1)、求每个大地球仪和每个小地球仪各多少元;(2)、昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪.26. 如图,在平面直角坐标系中,抛物线 , y与 轴交于A、B两点,与 轴交于点C.
 (1)、求点A、B、C的坐标;(2)、如图1,连接BC,点D是抛物线上一点,若∠DCB=∠ABC,求点D的坐标;(3)、如图2,若点P在以点O为圆心,OA长为半径作的圆上,连接BP、CP,请你直接写出 CP+BP的最小值.27. 如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB,BC所在的直线相交,交点分别为E,F.
(1)、求点A、B、C的坐标;(2)、如图1,连接BC,点D是抛物线上一点,若∠DCB=∠ABC,求点D的坐标;(3)、如图2,若点P在以点O为圆心,OA长为半径作的圆上,连接BP、CP,请你直接写出 CP+BP的最小值.27. 如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB,BC所在的直线相交,交点分别为E,F.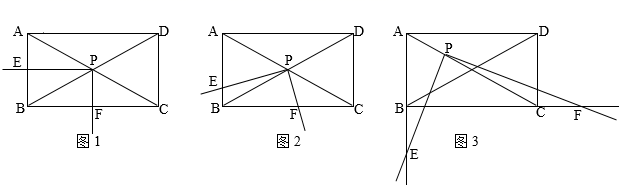 (1)、当PE⊥AB,PF⊥BC时,如图1,则 的值为 ;(2)、在(1)的基础上,现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;(3)、若与(2)相比只有如下变化,点P在线段AC上,且AP:PC=1:2,旋转角度α,满足60°<α<90°时,即如图3示, 的值是否变化?证明你的结论.
(1)、当PE⊥AB,PF⊥BC时,如图1,则 的值为 ;(2)、在(1)的基础上,现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;(3)、若与(2)相比只有如下变化,点P在线段AC上,且AP:PC=1:2,旋转角度α,满足60°<α<90°时,即如图3示, 的值是否变化?证明你的结论.