辽宁省沈阳市皇姑区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2023-05-12 类型:期末考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2020年,新冠病毒给世界各国带来了极大的灾难,中国在世界抗击新冠病毒疫情中发挥了重要作用.新冠病毒的整体尺寸一般在 ,请将 大的新冠病毒这个数用科学记数法表示为( )A、 B、 C、 D、3. 下列说法正确的是( )A、“购买1张彩票就中奖”是不可能事件 B、“概率为0.0001的事件”是不可能事件 C、“任意画一个三角形,它的内角和等于180°”是必然事件 D、任意掷一枚质地均匀的硬币10次,正面向上的一定是5次4. 在4 张相同的卡片上分别写有数1、3、4、6.将卡片的背面朝上并洗匀,从中抽取一张,抽到的数是奇数的概率( )A、 B、 C、 D、15. 如图,描述同位角、内错角、同旁内角关系不正确的是( )
2. 2020年,新冠病毒给世界各国带来了极大的灾难,中国在世界抗击新冠病毒疫情中发挥了重要作用.新冠病毒的整体尺寸一般在 ,请将 大的新冠病毒这个数用科学记数法表示为( )A、 B、 C、 D、3. 下列说法正确的是( )A、“购买1张彩票就中奖”是不可能事件 B、“概率为0.0001的事件”是不可能事件 C、“任意画一个三角形,它的内角和等于180°”是必然事件 D、任意掷一枚质地均匀的硬币10次,正面向上的一定是5次4. 在4 张相同的卡片上分别写有数1、3、4、6.将卡片的背面朝上并洗匀,从中抽取一张,抽到的数是奇数的概率( )A、 B、 C、 D、15. 如图,描述同位角、内错角、同旁内角关系不正确的是( )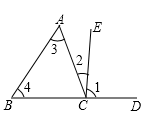 A、 与 是同位角 B、 与 是内错角 C、 与 是同旁内角 D、 与 是同旁内角6. 如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )
A、 与 是同位角 B、 与 是内错角 C、 与 是同旁内角 D、 与 是同旁内角6. 如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )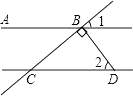 A、40° B、50° C、60° D、140°7. 三角形的三条高线的交点在三角形的一个顶点上,则此三角形是( )A、等腰三角形 B、锐角三角形 C、直角三角形 D、钝角三角形8. 一个三角形的两边长分别为4cm和5cm,则此三角形的第三边长不可能是( )A、3cm B、5cm C、7cm D、9cm9. 如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N , △BCN的周长是7cm,则BC的长为( )
A、40° B、50° C、60° D、140°7. 三角形的三条高线的交点在三角形的一个顶点上,则此三角形是( )A、等腰三角形 B、锐角三角形 C、直角三角形 D、钝角三角形8. 一个三角形的两边长分别为4cm和5cm,则此三角形的第三边长不可能是( )A、3cm B、5cm C、7cm D、9cm9. 如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N , △BCN的周长是7cm,则BC的长为( )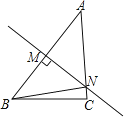 A、1cm B、2cm C、3cm D、4cm10. 如图,点O在AD上,∠A=∠C,∠AOC=∠BOD, AB=CD,AD=6,OB=2,则OC的长为( )
A、1cm B、2cm C、3cm D、4cm10. 如图,点O在AD上,∠A=∠C,∠AOC=∠BOD, AB=CD,AD=6,OB=2,则OC的长为( ) A、2 B、3 C、4 D、6
A、2 B、3 C、4 D、6二、填空题
-
11. 等腰三角形的一边长是12cm,另一边长是6cm,则它的周长是cm.12. 同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是y= x+32,如果某一温度的摄氏度数是25℃,那么它的华氏度数是℉.13. 如图,要测量池塘两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使A、C、E三点在一条直线上,这时测得的长就等于AB的长.
 14. 如图,AD、BE、CF是△ABC的三条中线,它们交于点O.若△ABD的面积是 , 则△ACF的面积是 .
14. 如图,AD、BE、CF是△ABC的三条中线,它们交于点O.若△ABD的面积是 , 则△ACF的面积是 . 15. 如图,在△ABC中,∠A=90°,∠ABC=60°,以顶点B为圆心,适当长为半径画弧,分别交边AB、BC于点E、F;再分别以E、F为圆心,以大于长为半径画弧,两弧交于点P,作射线BP,交AC边于点G.若△ABG的面积是 , 则△BCG的面积为 .
15. 如图,在△ABC中,∠A=90°,∠ABC=60°,以顶点B为圆心,适当长为半径画弧,分别交边AB、BC于点E、F;再分别以E、F为圆心,以大于长为半径画弧,两弧交于点P,作射线BP,交AC边于点G.若△ABG的面积是 , 则△BCG的面积为 . 16. 若三角形满足一个角是另一个角的3倍,则称这个三角形为“智慧三角形”,其中称为“智慧角”.在有一个角为60°的“智慧三角形”中,“智慧角”是度.
16. 若三角形满足一个角是另一个角的3倍,则称这个三角形为“智慧三角形”,其中称为“智慧角”.在有一个角为60°的“智慧三角形”中,“智慧角”是度.三、解答题
-
17. 简算:18. 计算:19. 先化简,再求值: , 其中x=1,y=-220. 按逻辑填写步骤和理由,将下面的证明过程补充完整
如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
求证: .

证明:∵∠1=∠2(已知)
∠ABF=∠1(对顶角相等)
∠BFG=∠2( )
∴∠ABF= ▲ (等量代换)
∵BE平分∠ABF(已知)
∴ ▲ ( )
∵FC平分∠BFG(已知)
∴ ▲ ( )
∴∠EBF= ▲
∴( )
21. 手机微信抢红包有多种玩法,其中一种为“拼手气红包”,用户设定好总金额以及红包个数后,可以随机生成不等金额的红包.现有一用户发了四个“拼手气红包”,随机被甲、乙、丙、丁四人抢到.(1)、以下说法正确的是____(直接填空);A、甲抢到的红包金额一定最多 B、乙抢到的红包金额一定最多 C、丙抢到的红包金额一定最多 D、丁不一定抢到金额最少的红包(2)、若这四个“拼手气红包”金额分别为35元、33元、20元、12元,则甲抢到红包的金额超过30元的概率是多少?22. 按逻辑填写步骤和理由,将下面的求解过程补充完整如图,在直角△ABC中,∠C=90°,AB的垂直平分线DE分别交AB、BC于点E、D.若 , 求∠B的度数.

解:设∠CAD=4x
∵(已知)
∴∠BAD=7x
∴ ▲ =∠BAD+∠CAD=11x
∵DE是AB的垂直平分线(已知)
∴DB= ▲ ( )
∴△ABD是等腰三角形
∴ ▲ =∠BAD=7x( )
∵△ABC是直角三角形,∠C=90°(已知)
∴∠B+∠BAC=90°( )
∴ ▲ + ▲ =90°
∴x= ▲
∴∠B= ▲
23. 一艘货船在甲、乙两港之间承接往返运输任务.某日货船从甲港顺流出发,途经丙港并不做停留,抵达乙港停留一段时间后逆流返航.货船在行驶过程中保持自身船速(即船在静水中的速度)不变,已知水流速度为8千米/时,如图记录了当日这艘货船出发后与乙港的距离y(千米)随时间t(小时)的变化的图象.图象上的点A表示货船当日顺流航行到达丙港. (1)、根据图象回答下列问题:货船在乙港停留的时间为小时,货船在静水中的速度为千米/时;(2)、m= , n=;(3)、货船当日顺流航行至丙港时,船上一救生圈不慎落入水中随水漂流,该货船能否在返航的途中找到救生圈?若能,请求出救生圈在水中漂流的时间;若不能,请说明理由.24. 如图①,在△ABC中,AB=AC=BC=10cm,动点P以每秒1cm的速度从点A出发,沿线段AB向点B运动.设点P的运动时间为t(t>0)秒.(知识储备:一个角是60°的等腰三角形是等边三角形)
(1)、根据图象回答下列问题:货船在乙港停留的时间为小时,货船在静水中的速度为千米/时;(2)、m= , n=;(3)、货船当日顺流航行至丙港时,船上一救生圈不慎落入水中随水漂流,该货船能否在返航的途中找到救生圈?若能,请求出救生圈在水中漂流的时间;若不能,请说明理由.24. 如图①,在△ABC中,AB=AC=BC=10cm,动点P以每秒1cm的速度从点A出发,沿线段AB向点B运动.设点P的运动时间为t(t>0)秒.(知识储备:一个角是60°的等腰三角形是等边三角形) (1)、当t=5时,求证:△PAC是直角三角形;(2)、如图②,若另一动点Q在线段CA上以每秒2cm的速度由点C向点A运动,且与点P同时出发,点Q到达终点A时点P也随之停止运动.当△PAQ是直角三角形时,直接写出t的值;(3)、如图③,若另一动点Q从点C出发,以每秒1cm的速度沿射线BC方向运动,且与点P同时出发.当点P到达终点B时点Q也随之停止运动,连接PQ交AC于点D,过点P作PE⊥AC于E.在运动过程中,线段DE的长度是否发生变化?若不变,直接写出DE的长度;若变化,说明如何变化.25. 在Rt△ABC中,∠BAC=90°,AC=AB,点D是直线BC上一点,过点A作∠DAE=90°(使点D,A,E按顺时针的顺序排列),且AE=AD,连接CE,过点A作AF⊥CE交直线CE于点F.
(1)、当t=5时,求证:△PAC是直角三角形;(2)、如图②,若另一动点Q在线段CA上以每秒2cm的速度由点C向点A运动,且与点P同时出发,点Q到达终点A时点P也随之停止运动.当△PAQ是直角三角形时,直接写出t的值;(3)、如图③,若另一动点Q从点C出发,以每秒1cm的速度沿射线BC方向运动,且与点P同时出发.当点P到达终点B时点Q也随之停止运动,连接PQ交AC于点D,过点P作PE⊥AC于E.在运动过程中,线段DE的长度是否发生变化?若不变,直接写出DE的长度;若变化,说明如何变化.25. 在Rt△ABC中,∠BAC=90°,AC=AB,点D是直线BC上一点,过点A作∠DAE=90°(使点D,A,E按顺时针的顺序排列),且AE=AD,连接CE,过点A作AF⊥CE交直线CE于点F. (1)、如图,当点D在线段BC上时;求证:CE=BD;(2)、当点D在直线BC上时,直接写出线段BD、CD、EF之间的数量关系.
(1)、如图,当点D在线段BC上时;求证:CE=BD;(2)、当点D在直线BC上时,直接写出线段BD、CD、EF之间的数量关系.