辽宁省沈阳市和平区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2023-05-12 类型:期末考试
一、单选题
-
1. 下列运算中,计算结果正确的是( )A、 B、 C、 D、2. 在以下“绿色食品、响应环保、可回收物、节水”四个标志图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列说法正确的是( )A、“在12名同学中有两人的生日在同一个月”是必然事件 B、“概率为0.0001的事件”是不可能事件 C、“射击运动员射击一次,命中靶心”是随机事件 D、任意掷一枚质地均匀的硬币20次,正面向上的次数一定是10次4. 以下列各组长度的线段为边,能构成三角形的是( )A、7cm、5cm、12cm B、6cm、8cm、10cm C、5cm、5cm、11cm D、4cm、10cm、3cm5. 某航班从机场出发,先在机场跑道上滑行加速,速度提升到一定程度后进行匀速爬升,爬升后保持一定高度飞行,一段时间后受到气流影响,于是匀速下降到一定高度保持飞行,到达目的地时进行匀速降落,最后经过机场跑道减速停机.下列能正确刻画这段时间内,飞机距离地面的高度h随时间t变化的图象的是( )A、
3. 下列说法正确的是( )A、“在12名同学中有两人的生日在同一个月”是必然事件 B、“概率为0.0001的事件”是不可能事件 C、“射击运动员射击一次,命中靶心”是随机事件 D、任意掷一枚质地均匀的硬币20次,正面向上的次数一定是10次4. 以下列各组长度的线段为边,能构成三角形的是( )A、7cm、5cm、12cm B、6cm、8cm、10cm C、5cm、5cm、11cm D、4cm、10cm、3cm5. 某航班从机场出发,先在机场跑道上滑行加速,速度提升到一定程度后进行匀速爬升,爬升后保持一定高度飞行,一段时间后受到气流影响,于是匀速下降到一定高度保持飞行,到达目的地时进行匀速降落,最后经过机场跑道减速停机.下列能正确刻画这段时间内,飞机距离地面的高度h随时间t变化的图象的是( )A、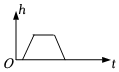 B、
B、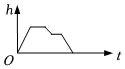 C、
C、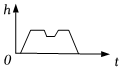 D、
D、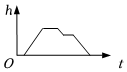 6. 如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
6. 如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )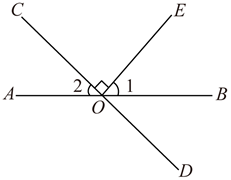 A、26° B、36° C、44° D、54°7. 某校七年级数学兴趣小组利用同一块长为1米的光滑木板,测量小车从不同高度沿的木板从顶部滑到底部所用的时间,支撑物的高度h(cm)与小车下滑时间t(s)之间的关系如下图所示:
A、26° B、36° C、44° D、54°7. 某校七年级数学兴趣小组利用同一块长为1米的光滑木板,测量小车从不同高度沿的木板从顶部滑到底部所用的时间,支撑物的高度h(cm)与小车下滑时间t(s)之间的关系如下图所示:支撑物高度h(cm)
10
20
30
40
50
60
70
小车下滑时间t(s)
4.23
3.00
2.45
2.13
1.89
1.71
1.59
根据表格所提供的信息,下列说法中错误的是( )
A、支撑物的高度为50cm,小车下滑的时间为1.89s B、支撑物的高度h越大,小车下滑时间t越小 C、若支撑物值高度每增加10cm,则对应的小车下滑时间的变化情况都相同 D、若小车下滑的时间为2.5s,则支撑物的高度在20cm至30cm之间8. 将图1边长为a的大正方形内,剪去一个边长为b的正方形,剩余部分(阴影部分)拼成一个长方形(如图2),这个过程是( )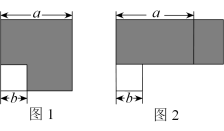 A、 B、 C、 D、9. 如图,小明在以∠A为顶角的等腰三角形ABC中用圆规和直尺作图,作出过点A的射线交BC于点D,然后又作出一条直线与AB交于点E,连接DE,若△BED的面积为4,则△ABC的面积为( )
A、 B、 C、 D、9. 如图,小明在以∠A为顶角的等腰三角形ABC中用圆规和直尺作图,作出过点A的射线交BC于点D,然后又作出一条直线与AB交于点E,连接DE,若△BED的面积为4,则△ABC的面积为( )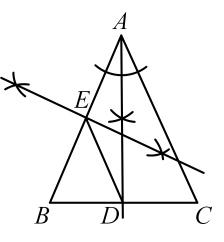 A、1 B、4 C、12 D、1610. 将一张长方形纸片按如图所示方式折叠,AE、AF为折痕,点B、D折叠后的对应点分别为、 , 若 , 则的度数为( )
A、1 B、4 C、12 D、1610. 将一张长方形纸片按如图所示方式折叠,AE、AF为折痕,点B、D折叠后的对应点分别为、 , 若 , 则的度数为( )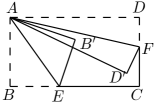 A、40.5° B、41° C、41.5° D、42°
A、40.5° B、41° C、41.5° D、42°二、填空题
-
11. 下列三个日常现象:

其中,可以用“垂线段最短”来解释的是 (填序号).
12. 如图,在中,BC边上的高是4cm,点D从点C出发,沿CB边向点B匀速运动,速度为0.1cm/s,连接AD,设动点D的运动时间为t(s)(点D到点B后停止运动),的面积为S(),则S与t之间的关系式为 .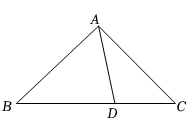 13. 转动如图所示的转盘,当转盘停止时,指针落在红色区域的概率是.
13. 转动如图所示的转盘,当转盘停止时,指针落在红色区域的概率是.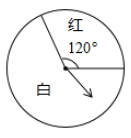 14. 在人类的大脑中,有一种神经元的半径约为25微米(1微米=米),将“25微米”用科学记数法表示为米.15. 如图,△AFD和△CEB,点A、E、F、C同一直线上,在给出的下列条件中,①AE=CF,②∠D=∠B,③AD=CB,④ , 选出三个条件可以证明的是 . (用序号表示,写出一种即可).
14. 在人类的大脑中,有一种神经元的半径约为25微米(1微米=米),将“25微米”用科学记数法表示为米.15. 如图,△AFD和△CEB,点A、E、F、C同一直线上,在给出的下列条件中,①AE=CF,②∠D=∠B,③AD=CB,④ , 选出三个条件可以证明的是 . (用序号表示,写出一种即可).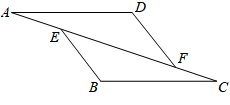 16. 三角形中,如果有一个内角是另外一个内角的4倍,我们把这个三角形叫做“四倍角三角形”.在一个“四倍角三角形”中有一个内角为40°,则另外两个角分别为 .17. 计算(3x+9)(6x+8)= .
16. 三角形中,如果有一个内角是另外一个内角的4倍,我们把这个三角形叫做“四倍角三角形”.在一个“四倍角三角形”中有一个内角为40°,则另外两个角分别为 .17. 计算(3x+9)(6x+8)= .三、解答题
-
18. 先化简,再求值: , 其中 , .19. 如图,在中, , 于点B,分别以点D和点B为圆心,以大于的长为半径作弧,两弧相交于点E和点F,作直线EF,延长AB交EF于点G,连接DG,下面是说明的说理过程,请把下面的推理过程及依据补充完整:理由如下:
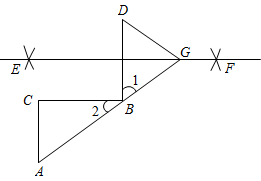
∵(已知)
∴∠DBC= ▲ (垂直的定义)
∵(已知)
∴∠DBC= ▲ (等量代换)
∴ ▲ ( )
∴∠1= ▲ ( )
由作图法可知:直线EF是线段DB的 ▲
∴GD= ▲ (线段垂直平分线上的点到这条线段两个端点的距离相等)
∴∠1=∠D(等腰三角形的两个底角相等)
∴∠A=∠D(等量代换)
20. 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黄球6个.(1)、从袋子里摸出一个球为红球的概率为;从袋子里摸出一个球为黄球的概率为;(2)、先从袋子中取出m个红球(m>1且m为正整数),再从袋子中随机摸一个小球,将“摸出黄球”记为事件A.①若事件A为必然事件,则m的值为;
②若事件A为随机事件,则m的值为 .
21. 尺规作图,已知 , 和线段a,作一个 , 使 , , (不写作法,保留作图痕迹,请不要在原来的图形上直接作图) 22. 如图,方格纸中每个小方格都是边长为1的正方形,我们把顶点均在格点上的三角形称为“格点三角形”,如图1,就是一个格点三角形.
22. 如图,方格纸中每个小方格都是边长为1的正方形,我们把顶点均在格点上的三角形称为“格点三角形”,如图1,就是一个格点三角形.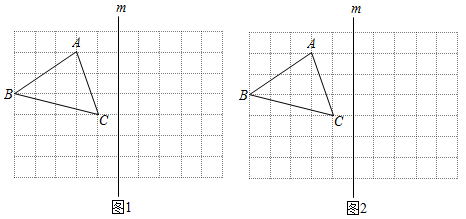
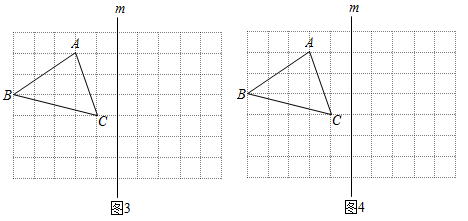 (1)、在图1中,作出关于直线m成轴对称的图形;并直接写出的面积为;(2)、在图2的直线m上求作点D,使得以A、C、D为顶点的格点三角形是以AC为腰的等腰三角形;(3)、在图3的直线m上找出一点E,使得EA+EC的值最小(保留作图痕定并标上字母E);(4)、在图4的直线m上找出一点F,使得的值最大(保留作图痕迹,并标上字母F).23. 填空:(将下面的推理过程补充完整)
(1)、在图1中,作出关于直线m成轴对称的图形;并直接写出的面积为;(2)、在图2的直线m上求作点D,使得以A、C、D为顶点的格点三角形是以AC为腰的等腰三角形;(3)、在图3的直线m上找出一点E,使得EA+EC的值最小(保留作图痕定并标上字母E);(4)、在图4的直线m上找出一点F,使得的值最大(保留作图痕迹,并标上字母F).23. 填空:(将下面的推理过程补充完整)已知:的高AD与高BE相交于点F,过点F作 , 交直线AB于点G.如图,若∠ABC=45°.
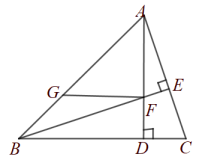
求证:(1);(2) .
(1)、∵AD,BE为△ABC的高,∴ ▲ ⊥BC,BE⊥AC,
∴ ▲ °,
∴ , , ▲ ,
∴ ,
∵∠ABC=45°,
∴ ▲ ,
∴ ,
∵在△FDB和△CDA中 , ∴;
(2)、∵ ▲ ,∴ ▲ ,
∴ ,
∴ ▲ ,
∴FA=FG,
∴ ▲ + ▲ .
24. 如图1,A,C两地之间有一条笔直的道路,B地位于A,C两地之间.甲从B地出发驾车驶往C地,乙从A地出发驾车驶向C地.在行驶过程中,乙由于汽车故障,换乘客车(换乘时间忽略不计)继续前行,并与甲同时到达C地.图2中线段MN和折线段PON分别表示甲、乙两人与A地的距离y(km)与甲行驶的时间x(h)的变化关系,其中MN与PQ交于点E.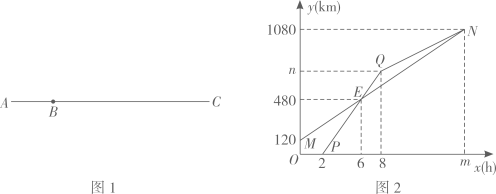 (1)、在图2中表示的自变量是 , 因变量是(2)、乙比甲晚出发h,B,C两地相距km;(3)、请直接写出甲的速度为;(4)、m= , n=;(5)、在图2中点E表示的含义是;(6)、请直接写出当x=h时,甲,乙相距30km.25. 如图1,在△ABC中,延长BC到D,使CD=AB,点E是BD下方一点,连接AE,DE,CE,且∠B=∠ACE=∠CDE.
(1)、在图2中表示的自变量是 , 因变量是(2)、乙比甲晚出发h,B,C两地相距km;(3)、请直接写出甲的速度为;(4)、m= , n=;(5)、在图2中点E表示的含义是;(6)、请直接写出当x=h时,甲,乙相距30km.25. 如图1,在△ABC中,延长BC到D,使CD=AB,点E是BD下方一点,连接AE,DE,CE,且∠B=∠ACE=∠CDE.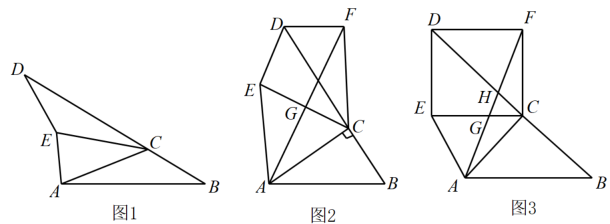 (1)、如图1,若∠D=30°,则∠CAE=度;(2)、如图2,若∠ACB=90°,AF=8cm,将DE沿直线CD翻折得到DF,连接CF,连接AF交CE于G,当时,求AG的长度;(3)、如图3,若AC=BC,将DE沿直线CD翻折得到DF,连接CF,连接AF交CE于G,交CD于H,若DF=m,AB=n,(),请直接写出线段CH的长度(用含m,n的代数式表示).
(1)、如图1,若∠D=30°,则∠CAE=度;(2)、如图2,若∠ACB=90°,AF=8cm,将DE沿直线CD翻折得到DF,连接CF,连接AF交CE于G,当时,求AG的长度;(3)、如图3,若AC=BC,将DE沿直线CD翻折得到DF,连接CF,连接AF交CE于G,交CD于H,若DF=m,AB=n,(),请直接写出线段CH的长度(用含m,n的代数式表示).