辽宁省葫芦岛市连山区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2023-05-12 类型:期末考试
一、单选题
-
1. 的算术平方根是( )A、2 B、4 C、±2 D、±42. 在平面直角坐标系中,点P(3,-2)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列调查中,适宜采用普查方式的是( )A、调查市场上冷冻食品的质量情况 B、调查乘坐飞机的旅客是否携带了违禁物品 C、调查某品牌冰箱的使用寿命 D、调查2021年春晚的收视率情况4. 如图,下列条件中,不能判定 的是( )
 A、 B、 C、 D、5. 不等式组 的解集在数轴上表示为( )A、
A、 B、 C、 D、5. 不等式组 的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 6. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=35°,则∠2等于( )
6. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=35°,则∠2等于( ) A、35° B、45° C、55° D、65°7. 中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有x个,甜果有y个,则可列方程组为( )A、 B、 C、 D、8. 下列说法中错误的是( )A、任何实数的绝对值都是非负数 B、不带根号的数是有理数 C、实数包括有理数和无理数 D、实数与数轴上的点之间是一一对应的9. 已知方程组的x,y满足x﹣y≥0,则m的取值范围是( )A、m≤﹣1 B、m≥﹣1 C、m≤1 D、m≥110. 如图// , 的平分线交于B,G是上的一点,的平分线交于点D,且 , 下列结论:①平分;②//;③与互余的角有2个;④若 , 则 . 其中正确的有( )
A、35° B、45° C、55° D、65°7. 中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有x个,甜果有y个,则可列方程组为( )A、 B、 C、 D、8. 下列说法中错误的是( )A、任何实数的绝对值都是非负数 B、不带根号的数是有理数 C、实数包括有理数和无理数 D、实数与数轴上的点之间是一一对应的9. 已知方程组的x,y满足x﹣y≥0,则m的取值范围是( )A、m≤﹣1 B、m≥﹣1 C、m≤1 D、m≥110. 如图// , 的平分线交于B,G是上的一点,的平分线交于点D,且 , 下列结论:①平分;②//;③与互余的角有2个;④若 , 则 . 其中正确的有( ) A、①② B、②④ C、①②③ D、①②④
A、①② B、②④ C、①②③ D、①②④二、填空题
-
11. 命题:“同角或等角的补角相等”是命题.(填“真”或“假”)12. 比较大小:3(填“>”、“<”或“=”).13. 有一个正的两位数,它的个位数字是十位数字的2倍小1,并且这个两位数不大于35,设十位数字为x,那么满足x的不等式组是 .14. 在平面直角坐标系的第四象限内有一个点M,到x轴的距离为4,到y轴的距离为1,则点M的坐标为 .15. 如果不等式组 的整数解共有 个,则a的取值范围是.16. 已知四边形ABCD,其中AD//BC,AB⊥BC,将DC沿DE折叠,C落于 , 交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点 (如图2),在两次折叠过程中,两条折痕DE、DF所成的角为度.


三、解答题
-
17. 计算.(1)、;(2)、 .18. 计算:(1)、解方程组: .(2)、解不等式组 ,并将不等式组的解集在数轴上表示出来.19. 如图,在平面直角坐标系中,点A,B,C的坐标分别是A(-2,-2),B(3,1),C(0,2).
 (1)、在图中画出△ABC向上平移3个单位,向右平移2个单位.(2)、写出点A1 , B1 , C1的坐标.(3)、求△ABC的面积.20. 某校为了解学生的课外阅读情况,对部分学生进行了调查,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制如下两幅不完整的统计图.
(1)、在图中画出△ABC向上平移3个单位,向右平移2个单位.(2)、写出点A1 , B1 , C1的坐标.(3)、求△ABC的面积.20. 某校为了解学生的课外阅读情况,对部分学生进行了调查,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制如下两幅不完整的统计图.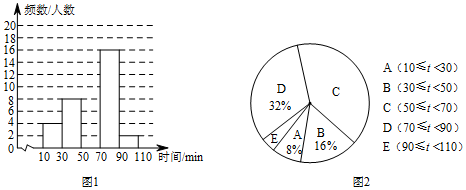
请你根据以上信息解答下列问题:
(1)、本次调查活动采取了什么调查方式,样本容量是多少?(2)、求图2中C的圆心角度数为度数,补全图1的频数分布直方图.(3)、该校有900名学生,估计该校学生平均每天的课外阅读时间不少于50min的人数.21. 如图,∠1=∠BCE,∠2+∠3=180°. (1)、判断AC与EF的位置关系,并说明理由;(2)、若CA平分∠BCE,EF⊥AB于点F,∠1=72°,求∠BAD的度数.22. 在疫情期间,学校购买甲、乙两种消毒液,已知购买3桶甲种消毒液和4桶乙种消毒液共需170元,购买2桶乙种消毒液比购买3桶甲种消毒液少用50元.(1)、求购买甲、乙两种消毒液每桶各需多少元?(2)、若要购买甲、乙两种消毒液共21桶,且总费用不超过548元,求至多可购进甲种消毒液多少桶?23. 已知关于x,y的二元一次方程ax+2y=a-1.(1)、若是该二元一次方程的一个解,求a的值;(2)、若x=2时,y>0,求a的取值范围;(3)、不论实数a(a≠0)取何值,方程ax+2y=a-1总有一个公共解,试求出这个公共解.24. 如图1,在平面直角坐标系中,坐标 , , 过作轴,垂足为 , 且满足
(1)、判断AC与EF的位置关系,并说明理由;(2)、若CA平分∠BCE,EF⊥AB于点F,∠1=72°,求∠BAD的度数.22. 在疫情期间,学校购买甲、乙两种消毒液,已知购买3桶甲种消毒液和4桶乙种消毒液共需170元,购买2桶乙种消毒液比购买3桶甲种消毒液少用50元.(1)、求购买甲、乙两种消毒液每桶各需多少元?(2)、若要购买甲、乙两种消毒液共21桶,且总费用不超过548元,求至多可购进甲种消毒液多少桶?23. 已知关于x,y的二元一次方程ax+2y=a-1.(1)、若是该二元一次方程的一个解,求a的值;(2)、若x=2时,y>0,求a的取值范围;(3)、不论实数a(a≠0)取何值,方程ax+2y=a-1总有一个公共解,试求出这个公共解.24. 如图1,在平面直角坐标系中,坐标 , , 过作轴,垂足为 , 且满足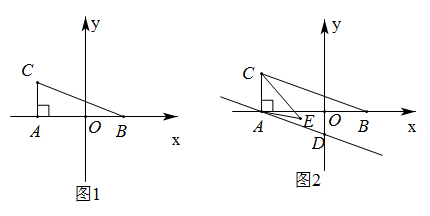 (1)、求三角形的面积;(2)、若过作交轴于 , 且 , 分别平分 , , 如图2,直接写出的度数;(3)、在轴上存在一点 , 使得三角形和三角形的面积相等,直接写出点的坐标.25. 如图1,点A在直线MN上,点B在直线ST上,点C在MN,ST之间,且满足∠MAC+∠ACB+∠SBC=360°.
(1)、求三角形的面积;(2)、若过作交轴于 , 且 , 分别平分 , , 如图2,直接写出的度数;(3)、在轴上存在一点 , 使得三角形和三角形的面积相等,直接写出点的坐标.25. 如图1,点A在直线MN上,点B在直线ST上,点C在MN,ST之间,且满足∠MAC+∠ACB+∠SBC=360°. (1)、证明:;(2)、如图2,若∠ACB=60°, , 点E在线段BC上,连接AE,且∠DAE=2∠CBT,试判断∠CAE与∠CAN的数量关系,并说明理由;(3)、如图3,若∠ACB=45°,点E在线段BC上,连接AE,若∠MAE=4∠CBT,直接写出∠CAE:∠CAN的值.
(1)、证明:;(2)、如图2,若∠ACB=60°, , 点E在线段BC上,连接AE,且∠DAE=2∠CBT,试判断∠CAE与∠CAN的数量关系,并说明理由;(3)、如图3,若∠ACB=45°,点E在线段BC上,连接AE,若∠MAE=4∠CBT,直接写出∠CAE:∠CAN的值.