吉林省长春市长春汽车经济技术开发区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-05-12 类型：期末考试

进入出卷网下载

一、单选题

1. 4的平方根是（）

A、4 B、±4 C、±2 D、2

查看试题解析
2. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 一元一次方程 $8 x = 2 x - 6$ 的解是（）

A、 $x = 1$ B、 $x = 0$ C、 $x = - 2$ D、 $x = - 1$

查看试题解析
4. 不等式组 ${\begin{array}{l} 2 x - 2 \geq 0 ， \\ x - 3 < 0 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 一个多边形的内角和等于 $2160 °$ ，则这个多边形是（）

A、八边形 B、十边形 C、十一边形 D、十四边形

查看试题解析
6. 若三角形的两边长分别为4和7，则该三角形的周长可能为（）

A、9 B、14 C、18 D、22

查看试题解析
7. 下列生活中的一些事实运用了“三角形稳定性”的是（）

A、 B、 C、 D、

查看试题解析
8. 我国古代数学著作《增删算法统宗》中有这么一首诗：“今有布绢四十定，共卖价钞六百八．四定绢价九十贯，三定布价该五十．欲问绢布各几何？价钞各该分端，若人算得无差讹，堪把芳名题郡邑．”其大意是：今有绢与布40定，卖得680贯钱，4定绢价90贯，3定布价50贯，欲问绢布有多少，分开把价算，若人算得无差错，你的名字城镇到处扬．设有绢 $x$ 定，布 $y$ 定，依据题意可列方程组为（）

A、 ${\begin{array}{l} x + y = 40 \\ \frac{90}{4} x + \frac{50}{3} y = 680 \end{array}$ B、 ${\begin{array}{l} x + y = 40 \\ \frac{90}{3} x + \frac{50}{4} y = 680 \end{array}$ C、 ${\begin{array}{l} x + y = 40 \\ \frac{90}{3} y + \frac{50}{4} x = 680 \end{array}$ D、 ${\begin{array}{l} x + y = 40 \\ \frac{50}{3} x + \frac{90}{4} y = 680 \end{array}$

查看试题解析

二、填空题

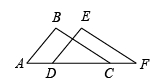
9. 把方程 $3 x + y = 17$ 改写成用含x的式子表示y的形式，则 $y =$ ．

查看试题解析
10. 将“a的2倍与4的差是非负数”用不等式表示为.

查看试题解析
11. 比较大小： $\sqrt{3}$ $\sqrt{2}$ ．（填“>”“<”或“＝”）

查看试题解析
12. 如图，将 $△ A B C$ 沿AC的方向平移至 $△ D E F$ ，若图中AC＝12，DC＝9，则CF的长为.

查看试题解析
13. 如图， $△ A B C ≌ △ D E B$ ，点E在边AB上，DE与AC相交于点F．若 $∠ D = 35 °$ ， $∠ C = 60 °$ ，则∠AFD的大小为度．

查看试题解析
14. 如图，点P是∠AOB内一点，点P关于OA的对称点为C，点P关于OB的对称点为D，连接CD交OA、OB于点M和点N，连接PM、PN．若 $∠ A O B = 50 °$ ，则 $∠ M P N$ 的大小为度．

查看试题解析

三、解答题

15.

(1)、解方程： $3 (x - 2) - (1 - 2 x) = 3$ ．

(2)、解不等式： $2 x - 1 < 4 x + 3$ .

查看试题解析
16. 解方程组： ${\begin{array}{l} x - y = - 5 \\ 3 x + 2 y = 10 \end{array}$

查看试题解析
17. 解不等式组： ${\begin{array}{l} \frac{x - 1}{2} \geq \frac{x - 2}{3} ， \\ 2 x - 5 < - 3 x . \end{array}$ 并写出它的所有整数解．

查看试题解析
18. 已知正n边形的每个内角与其外角的差为90°，求这个多边形的每个内角度数与边数n．

查看试题解析
19. 如图，在△ABC中，∠B=36°，∠ACB=110°，AE是∠BAC的平分线，AD是BC边上的高，求∠DAE的度数.

查看试题解析
20. 图①、图②均是10×10的方格纸， $△ A B C$ 的顶点均在格点上．只用无刻度的直尺，在给定的网格中按要求作图，保留适当的作图痕迹．

(1)、先在图①中，画出 $△ A_{1} B_{1} C_{1}$ ，使 $△ A_{1} B_{1} C_{1}$ 和 $△ A B C$ 关于点O成中心对称．

(2)、在图②中，将 $△ A B C$ 绕点B顺时针旋转90°，画出旋转后的 $△ A_{2} B C_{2}$ ．

查看试题解析
21. 已知正数 $a + b - 5$ 的平方根是 $\pm 3$ ， $a - b + 4$ 的立方根是2．

(1)、求a和b的值．

(2)、求 $5 a + 4 b - 1$ 的立方根．

查看试题解析
22. 2022年第19届亚运会即将在我国杭州举行．如图①是杭州亚运会马术项目比赛场馆桐庐马术中心，其总建筑面积约为5.4万平方米，包括各种功能区．为了确保参赛马匹拥有舒适的居住环境，每匹马都有自己的“单人间”，即高标准马厩（如图②），中心设置了约240个高标准马厩．其中主赛场和马厩总共占16320平方米，主赛场面积是马厩的2倍还多3360平方米．求主赛场和“单人间”的面积各多少平方米？

查看试题解析
23. 实践与探究
材料：锐角三角形卡纸ABC，正方形卡纸DEFG．

(1)、操作一：如图①，将 $△ A B C$ 放置在正方形卡纸DEFG上，使点D在 $△ A B C$ 内，点B、C分别在边DG和边DE上．
若 $∠ A = 40 °$ ，则∠ABC＋∠ACB＝°，∠DBC＋∠DCB＝°，∠ABD＋∠ACD＝°．

(2)、请你探究∠ABD＋∠ACD与∠A之间的数量关系，并说明理由．
操作二：如图②，改变正方形卡纸DEFG的位置，使点D在 $△ A B C$ 外，且在AB边的左侧，点B、C分别在边DG和边DE上，则∠ABD、∠ACD与∠A的数量关系为

查看试题解析
24. 已知数轴上的原点为O，A、B、C三点对应的数分别为 $- 16$ ， 8和12，动点P从点A出发，以每秒2个单位的速度沿数轴正方向运动，同时，动点Q从点C出发，以每秒1个单位的速度沿数轴负方向运动，设点P的运动时间为t秒．

(1)、线段AB的长为，线段AC的长为

(2)、当点P运动到与点A、B距离相等时，求点P表示的数．

(3)、当P、Q两点相遇时，求t的值．

(4)、当PO＋QB＝10时，直接写出t的值．

查看试题解析