吉林省长春市榆树市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2023-05-12 类型:期末考试
一、单选题
-
1. 方程的解是( )A、 B、 C、 D、2. 下列标志中,是轴对称图形的是( )A、
 节水标志
B、
节水标志
B、 生产许可
C、
生产许可
C、 绿色食品
D、
绿色食品
D、 回收标志
3. 下列方程变形正确的是( )A、由 ,得 B、由 ,得 C、由 ,得 D、由 ,得4. 如图,沿射线方向平移到的位置,若 , 则的长度为( )
回收标志
3. 下列方程变形正确的是( )A、由 ,得 B、由 ,得 C、由 ,得 D、由 ,得4. 如图,沿射线方向平移到的位置,若 , 则的长度为( ) A、 B、 C、 D、5. 只用下列正多边形地砖中的一种,能够铺满地面的是( )A、正五边形 B、正六边形 C、正八边形 D、正十边形6. 《九章算术》中有一道题的条件是:“今有大器五小器一容三斛,大器一小器五容二斛。”大致意思是:有大小两种盛米的桶,5大桶加1小桶共盛3斛米,1大桶加5小桶共盛2斛米,依据该条件,若设1个大桶可以盛米x斛,1个小桶可以盛米y斛,则可列方程组为( )A、 B、 C、 D、7.
A、 B、 C、 D、5. 只用下列正多边形地砖中的一种,能够铺满地面的是( )A、正五边形 B、正六边形 C、正八边形 D、正十边形6. 《九章算术》中有一道题的条件是:“今有大器五小器一容三斛,大器一小器五容二斛。”大致意思是:有大小两种盛米的桶,5大桶加1小桶共盛3斛米,1大桶加5小桶共盛2斛米,依据该条件,若设1个大桶可以盛米x斛,1个小桶可以盛米y斛,则可列方程组为( )A、 B、 C、 D、7.已知,AC∥ED,∠C=26°,∠CBE=37°,则∠BED的度数是( )
 A、53° B、63° C、73° D、83°8. 如图,六边形 内部有一点 ,连结 .若 ,则 的大小为( )
A、53° B、63° C、73° D、83°8. 如图,六边形 内部有一点 ,连结 .若 ,则 的大小为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若a<b,那么﹣2a+9 ﹣2b+9(填“>”“<”或“=”).10. 不等式2x-3≤3的正整数解是 .11. 已知 是等腰三角形,若它的周长为18,一条边的长为4,则它的腰长为 .12. 若正多边形的一个外角的度数为40°,则这个正多边形是边形.13. 在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是 . .
 14. 如图,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为 .
14. 如图,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为 .

三、解答题
-
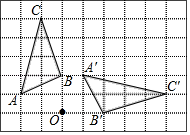
15. 解下列方程: .16. 解方程组:17. 如图,在的正方形网格中,的三个顶点和点都在格点上,按要求画一个三角形,使它的顶点均在格点上.
 (1)、将在网格内平移,在图①中画出平移后的三角形,使点落在其内部.(2)、以点为旋转中心,将旋转,在图②中画出旋转后的三角形,使点落在其内部.18. 解不等式组: 并将解集在数轴上表示.19. 对于下列问题,在解答过程的空白处填上适当的内容(理由或数学式).如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°.
(1)、将在网格内平移,在图①中画出平移后的三角形,使点落在其内部.(2)、以点为旋转中心,将旋转,在图②中画出旋转后的三角形,使点落在其内部.18. 解不等式组: 并将解集在数轴上表示.19. 对于下列问题,在解答过程的空白处填上适当的内容(理由或数学式).如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°. (1)、求∠EBC的度数;(2)、求∠A的度数.
(1)、求∠EBC的度数;(2)、求∠A的度数.解:∵CD⊥AB(已知),
∴∠CDB= ▲ °
∵∠EBC=∠CDB+∠BCD( ).
∴∠EBC= ▲ °+35°= ▲ °(等量代换).
∵∠EBC=∠A+∠ACB( ),
∴∠A=∠EBC-∠ACB(等式的性质)
∵∠ACB=90°(已知),
∴∠A= ▲ -90°= ▲ °(等量代换).
20. 如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上. (1)、若BE⊥AD,∠F=62°,求∠A的大小.(2)、若AD=9cm,BC=5cm,求AB的长.21. 榆树市某中学七年一班全体学生参加社团活动进行分组,原来每组8人,后来重新编组,每组12人,这样就比原来减少2组,请问七年一班共有多少人?22. 如图,在中,是边上的中线,的周长比的周长多1,AB与AC的和为11
(1)、若BE⊥AD,∠F=62°,求∠A的大小.(2)、若AD=9cm,BC=5cm,求AB的长.21. 榆树市某中学七年一班全体学生参加社团活动进行分组,原来每组8人,后来重新编组,每组12人,这样就比原来减少2组,请问七年一班共有多少人?22. 如图,在中,是边上的中线,的周长比的周长多1,AB与AC的和为11 (1)、求、的长;(2)、求边的取值范围.
(1)、求、的长;(2)、求边的取值范围.
