吉林省长春市宽城区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2023-05-12 类型:期末考试
一、单选题
-
1. 4的平方根是( )A、 ±2 B、2 C、﹣2 D、162. 下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )A、
 医疗废物
B、
医疗废物
B、 中国红十字会
C、
中国红十字会
C、 医疗卫生服务机构
D、
医疗卫生服务机构
D、 国际急救
3. 在实数0, , , 中,最大的实数是( )A、0 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、
国际急救
3. 在实数0, , , 中,最大的实数是( )A、0 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、 B、
B、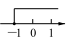 C、
C、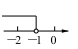 D、
D、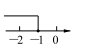 5. 若一个正多边形的一个外角是60°,则这个正多边形的边数是( )A、10 B、9 C、8 D、66. 古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,若设这个数是 ,则所列方程为( )A、 B、 C、 D、7. 一个正方形水池的四周恰好被4个完全相同的正n边形地砖铺满,其部分示意图如图所示,则n的值为( )
5. 若一个正多边形的一个外角是60°,则这个正多边形的边数是( )A、10 B、9 C、8 D、66. 古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,若设这个数是 ,则所列方程为( )A、 B、 C、 D、7. 一个正方形水池的四周恰好被4个完全相同的正n边形地砖铺满,其部分示意图如图所示,则n的值为( )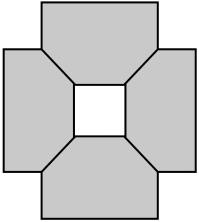 A、6 B、8 C、10 D、128. 如图,在 中, , ,将 绕点C顺时针旋转90°得到 ,点B的对应点 在边 上(不与点A , C重合),则 的度数为( )
A、6 B、8 C、10 D、128. 如图,在 中, , ,将 绕点C顺时针旋转90°得到 ,点B的对应点 在边 上(不与点A , C重合),则 的度数为( )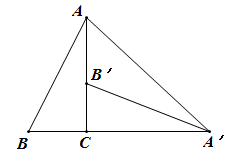 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 化简: = .10. 已知一个三角形的两边长分别为2和5,若第三边的长为整数,则第三边的长可以为(写出一个即可)11. 比较大小: 5(选填“ ”、“ ”、“ ” ).12. 已知 是方程 的一个解,则m的值是.13. 将一副三角板按如图所示的方式摆放,点D在边AC上, ,则 的大小为度.
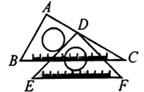 14. 如图, , 点A和点D是对应顶点,点B和点E是对应顶点,过点A作于点F.若∠BCE=65°,则∠CAF的大小为度.
14. 如图, , 点A和点D是对应顶点,点B和点E是对应顶点,过点A作于点F.若∠BCE=65°,则∠CAF的大小为度.
三、解答题
-
15. 计算:.16. 解方程组: .17. 解不等式组: , 并将解集在数轴上表示.18. 如图所示的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1个单位,△ABC的三个顶点均在格点上.要求只用无刻度的直尺,在给定的网格中按要求画图,保留作图痕迹.
 (1)、在网格中画出△ABC向下平移3个单位得到的 .(2)、在网格中画出△ABC关于直线m成轴对称的 .(3)、在直线m上画一点P,使得的值最小.19. 自动驾驶汽车是一种通过电脑系统实现无人驾驶的智能汽车,某出租车公司拟在今明两年共投资6000万元改造220辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改造费用是30万元,预计明年每辆无人驾驶出租车的改造费用可下降40%.(1)、求明年每辆无人驾驶出租车的改造费用.(2)、求今年改造的无人驾驶出租车的数量.20. 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)、在网格中画出△ABC向下平移3个单位得到的 .(2)、在网格中画出△ABC关于直线m成轴对称的 .(3)、在直线m上画一点P,使得的值最小.19. 自动驾驶汽车是一种通过电脑系统实现无人驾驶的智能汽车,某出租车公司拟在今明两年共投资6000万元改造220辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改造费用是30万元,预计明年每辆无人驾驶出租车的改造费用可下降40%.(1)、求明年每辆无人驾驶出租车的改造费用.(2)、求今年改造的无人驾驶出租车的数量.20. 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.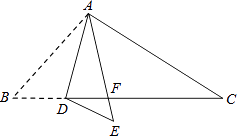 (1)、填空:∠AFC=度;(2)、求∠EDF的度数.21. 我们把关于x、y的两个二元一次方程x+ky=b与kx+y=b(k≠1)叫做互为共轭二元一次方程;二元一次方程组叫做共轭二元一次方程组.(1)、若关于x、y的方程组为共轭方程组,则a= , b= .(2)、解下列方程组(直接写出方程组的解即可):
(1)、填空:∠AFC=度;(2)、求∠EDF的度数.21. 我们把关于x、y的两个二元一次方程x+ky=b与kx+y=b(k≠1)叫做互为共轭二元一次方程;二元一次方程组叫做共轭二元一次方程组.(1)、若关于x、y的方程组为共轭方程组,则a= , b= .(2)、解下列方程组(直接写出方程组的解即可):的解为;的解为 .
(3)、发现:若共轭方程组的解是则m、n之间的数量关系是 .22. 如图,AD为△ABC的高,AE、BF为△ABC的角平分线,∠CBF=30°,∠AFB=70°. (1)、∠BAD=度.(2)、求∠DAE的度数.(3)、若点M为线段BC上任意一点,当△MFC为直角三角形时,直接写出∠BFM的度数.23. 小李在某网店选中A、B两款玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
(1)、∠BAD=度.(2)、求∠DAE的度数.(3)、若点M为线段BC上任意一点,当△MFC为直角三角形时,直接写出∠BFM的度数.23. 小李在某网店选中A、B两款玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:类别
A款玩偶
B款玩偶
进货价(元/个)
40
30
销售价(元/个)
56
45
(1)、第一次小李用1100元购进了A、B两款玩偶共30个,求这两款玩偶各购进的数量.(2)、第二次小李进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小李计划购进这两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?请通过计算说明.24. 【教材呈现】以下是华师版七年级下册数学教材第122页的部分内容:如图①,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,画出△ACE以点A为旋转中心、逆时针旋转90°后的三角形.
 (1)、【操作发现】在图①中画出△ACE以点A为旋转中心、逆时针旋转90°后的三角形,写出旋转前后CE与其对应线段的数量关系和位置关系:。(2)、【探究证明】如图②,将△ACE绕点A逆时针旋转90°得到△ADB,设CE、AC分别与BD交于点F、G,判断CE和DB的数量关系和位置关系,并说明理由.(3)、【问题解决】如图③,将△ABC绕点A逆时针旋转40°得到△ADE,点D恰好落在BC上,DE与CA交于点F.若△ABD与△AFD关于直线AD对称,且BC=9,BD=3,则:
(1)、【操作发现】在图①中画出△ACE以点A为旋转中心、逆时针旋转90°后的三角形,写出旋转前后CE与其对应线段的数量关系和位置关系:。(2)、【探究证明】如图②,将△ACE绕点A逆时针旋转90°得到△ADB,设CE、AC分别与BD交于点F、G,判断CE和DB的数量关系和位置关系,并说明理由.(3)、【问题解决】如图③,将△ABC绕点A逆时针旋转40°得到△ADE,点D恰好落在BC上,DE与CA交于点F.若△ABD与△AFD关于直线AD对称,且BC=9,BD=3,则:①∠DAE=度;
②∠CDE=度;
③线段EF的长是 .