吉林省长春市二道区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2023-05-12 类型:期末考试
一、单选题
-
1. 方程的解为( )A、-1 B、1 C、3 D、-32. 剪纸艺术是中国最具特色的民间艺术之一,其中蕴含着极致的数学美.下列剪纸图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 不等式的解集在数轴上表示正确的是( )A、
3. 不等式的解集在数轴上表示正确的是( )A、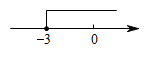 B、
B、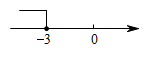 C、
C、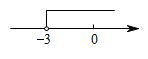 D、
D、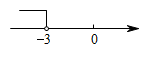 4. 下列正多边形中和正三角形组合,不能铺满地面的是( )A、正方形 B、正八边形 C、正十二边形 D、正六边形5. 用一根长的细铁丝围成一个三角形,其中三边的长(单位:)分别为整数、、 , 且 , 则最大可取( )A、4 B、5 C、6 D、76. 如图,将沿射线方向平移 , 得到 , 点落在线段上.若的周长为 , 则四边形的周长为( )
4. 下列正多边形中和正三角形组合,不能铺满地面的是( )A、正方形 B、正八边形 C、正十二边形 D、正六边形5. 用一根长的细铁丝围成一个三角形,其中三边的长(单位:)分别为整数、、 , 且 , 则最大可取( )A、4 B、5 C、6 D、76. 如图,将沿射线方向平移 , 得到 , 点落在线段上.若的周长为 , 则四边形的周长为( )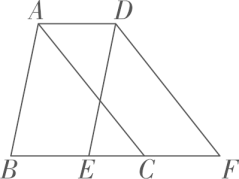 A、 B、 C、 D、7. 将一副三角板按如图所示的方式摆放,其中点落在边上,点落在边上,则的大小为( )
A、 B、 C、 D、7. 将一副三角板按如图所示的方式摆放,其中点落在边上,点落在边上,则的大小为( ) A、 B、 C、 D、8. 《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊各几何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元,求人数和羊价各是多少?设买羊人数为x人,根据题意可列方程为( )A、 B、 C、 D、
A、 B、 C、 D、8. 《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊各几何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元,求人数和羊价各是多少?设买羊人数为x人,根据题意可列方程为( )A、 B、 C、 D、二、填空题
-
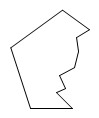
9. 关于x的方程的解与方程的解相同,则a的值是 .10. 已知方程 , 用含的式子表示 , 则 .11. 不等式组的解集是 .12. 如图是一个正多边形的玻璃碎片,这个正多边形的边数为 .
 13. 如图, , 若 , 则度.
13. 如图, , 若 , 则度.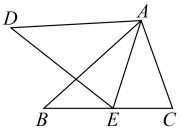 14. 如图是一张三角形纸片 , , , 是边上的一点,是边上的一点,将沿折叠,使点落在点处,若 , 则度.
14. 如图是一张三角形纸片 , , , 是边上的一点,是边上的一点,将沿折叠,使点落在点处,若 , 则度.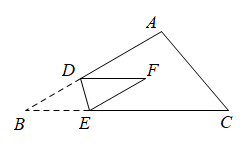
三、解答题
-
15. 解方程: .16. 解一元一次不等式: .17. 一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.
18. 如图,在中,是边上一点,是边上一点,和相交于点 , , , .
求:
(1)、的度数;(2)、的度数,对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
解:∵( ),
∴ (等量代换).
∵ ▲ ( ),
∴ ▲ (等式的性质)
(等量代换)
= ▲ .
19. 下面是马小虎同学解二元一次方程组的过程,请认真阅读并完成相应的任务.解方程组:
解:①×2,得……③ 第一步
②-③,得 第二步
. 第三步
将代入①,得 . 第四步
所以,原方程组的解为第五步
(1)、这种求解二元一次方程组的方法叫做法,以上求解步骤中,马小虎同学第步开始出现错误.(2)、请写出此题正确的解答过程.20. 如图,和均为等边三角形,点、、在同一直线上,连结 . 试说明 . 聪明的小亮很快就找到了解决该问题的方法,请你帮助小亮把说理过程补充完整.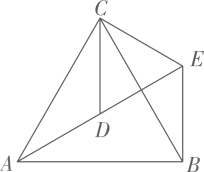
解:∵和均为等边三角形,
∴ , , ▲ (等边三角形的性质),
∴ ▲ ,
即绕点按逆时针方向旋转 ▲ 度,能够与 ▲ 重合,
∴ (旋转变换的性质),
∴( ).
21. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,点、、、、、均为格点,只用无刻度的直尺,按下列要求作图: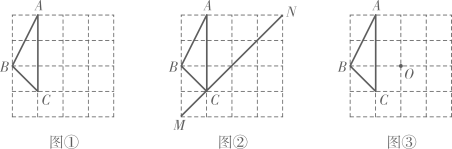 (1)、在图①中,画出图中向右平移3格后的;(2)、在图②中,画出图中关于直线对称的;(3)、在图③中,画出图中绕点顺时针旋转后的 .22. 【阅读感悟】
(1)、在图①中,画出图中向右平移3格后的;(2)、在图②中,画出图中关于直线对称的;(3)、在图③中,画出图中绕点顺时针旋转后的 .22. 【阅读感悟】有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
已知实数、满足……①,……②,求和的值.
本题常规思路是将①②两式联立组成方程组,解得、的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形,整体求得代数式的值,如由①-②可 , 由①+②×2可得 . 这样的解题思想就是通常所说的“整体思想”.
【解决问题】
(1)、已知二元一次方程组 , 求和的值;(2)、初二(3)班组织书法比赛,要购买一些学习用品用于发奖,若买20支铅笔、3块橡皮、2本日记本共需33元,买39支铅笔、5块橡皮、3本日记本共需60元,则购买2支铅笔、2块橡皮、2本日记本共需多少元?(3)、对于实数、 , 定义新运算: , 其中、、是常数,等式右边是通常的加法和乘法运算.已知 , , 求的值.23. 模型认识:我们学过三角形的内角和等于 , 又知道角平分线可以把一个角分成大小相等的两部分,接下来我们就利用上述知识进行下面的探究活动.如图①,在中,、分别是和的角平分线.
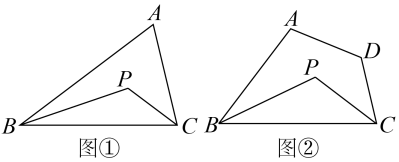 (1)、解决问题:
(1)、解决问题:若 , , 则;(直接写出答案)
(2)、若 , 求出的度数;(3)、拓展延伸:如图②,在四边形中,、分别是和的角平分线,直接写出与的数量关系.
24. 如图,在长方形中, , . 点从点出发,沿折线以每秒2个单位的速度向点运动,同时点从点出发,沿以每秒1个单位的速度向点运动,当点到达点时,点、同时停止运动.设点的运动时间为秒.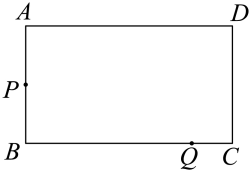 (1)、当点在边上运动时,(用含的代数式表示);(2)、当点与点重合时,求的值;(3)、当时,求的值;(4)、若点关于点的中心对称点为点 , 直接写出和面积相等时的值.
(1)、当点在边上运动时,(用含的代数式表示);(2)、当点与点重合时,求的值;(3)、当时,求的值;(4)、若点关于点的中心对称点为点 , 直接写出和面积相等时的值.