吉林省四平市铁东区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-05-12 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，已知 $a ∥ b$ ，直线 $l$ 与 $a ， b$ 相交.若 $∠ 1 = 60 °$ ，则 $∠ 2 =$ （）

A、 $120 °$ B、 $30 °$ C、 $100 °$ D、 $60 °$

查看试题解析
2. 如图，在下列的条件中，能判定DE∥AC的是（）

A、 $∠ 1 = ∠ 4$ B、 $∠ 1 = ∠ A$ C、 $∠ A = ∠ 3$ D、 $∠ A + ∠ 2 = 180 °$

查看试题解析
3. $\sqrt{81}$ 的平方根是（）

A、 $\pm 9$ B、3 C、 $\pm 3$ D、 $- 3$

查看试题解析
4. 不等式 $2 (x - 2) \leq x - 1$ 的非负整数解的个数为（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
5. 已知 $P (- 2 ， - 3)$ 到 $x$ 轴的距离是（）

A、 $2$ B、 $3$ C、 $- 3$ D、 $- 2$

查看试题解析
6. 如图，四边形ABCD中，点M，N分别在AB，BC上，∠A＝100°，∠C＝70°，将△BMN沿MN翻折，得△FMN，若MF $∥$ AD，FN $∥$ DC，则∠B的度数为（）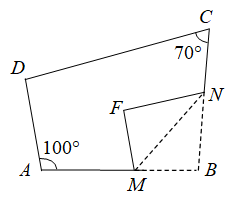

A、80° B、85° C、90° D、95°

查看试题解析

二、填空题

7. $- \frac{1}{27}$ 的立方根是.

查看试题解析
8. 若点 $P (a - 1 ， 3 a + 6)$ 位于第二象限，则的 $a$ 取值范围是．

查看试题解析
9. 已知 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ ，是方程组 ${\begin{array}{l} 2 x + m y = 4 \\ n x - 2 y = - 7 \end{array}$ 的解，则 $m + n =$ .

查看试题解析
10. 有这样一个故事：一匹马和一头驴驮着不同袋数的货物一同走，每袋货物的重量相同，驴抱怨负担太重，马说：“你抱怨啥？如果你给我一袋，那么我的负担是你的2倍；如果我给你一袋，我们才恰好一样多！”那么驴原来所驮货物有袋．

查看试题解析
11. 已知a为 $\sqrt{17}$ 的整数部分， $b$ -1是400的算术平方根，则 $\sqrt{a + b}$ 的值为．

查看试题解析
12. 北京市为了全民健身，举办“健步走”活动，活动场地位于奥林匹克公园（路线：森林公园→玲珑塔→国家体育场→水立方）．如果体育局的工作人员在奥林匹克公园设计图上标记玲珑塔的坐标为 $(- 1 ， 0)$ ，森林公园的坐标为 $(- 2 ， 3) ，$ 则终点水立方的坐标是．

查看试题解析
13. 如图，将周长为 $2 \sqrt{2} + 3$ 的 $△ A B C$ 沿 $B C$ 方向平移 $2$ 个单位得到 $△ D E F ，$ 则四边形 $A B F D$ 的周长为．

查看试题解析
14. 如图，AB∥CD，直线EF分别交AB、CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于度．

查看试题解析

三、解答题

15. 计算： $\sqrt{81} + \sqrt[3]{- 27} + \sqrt{{(- \frac{2}{3})}^{2}}$ ．

查看试题解析
16. 解方程组： ${\begin{array}{l} (x - 2) + 2 (y + 1) = 7 \\ \frac{x + 1}{3} - \frac{y}{6} = 1 \end{array}$

查看试题解析
17. 解不等式组： ${\begin{array}{l} 3 x - (x - 2) ⩽ 6 \\ x - 1 < \frac{4 x + 1}{3} \end{array}$ 并将解集在数轴上表示．

查看试题解析
18. 已知一个数的两个平方根分别是 $3 a + 2$ 和 $a + 14$ ，求这个数的立方根.

查看试题解析
19. 在如图所示的平面直角坐标系中，每个小方格都是边长为1的正方形， $△ A B C$ 的顶点均在格点上，点A的坐标是 $(- 3 ， - 1)$ ．

(1)、将 $△ A B C$ 沿y轴正方向平移3个单位得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ 并求出点B₁坐标；

(2)、求四边形 $A B C C_{1}$ 的面积．

查看试题解析
20. 如图，已知： $D C ∥ F P$ ， ∠1＝∠2，∠DEF＝30°，∠AGF＝80°，FH平分∠EFG．

(1)、求证： $D C ∥ A B$ ；

(2)、求∠PFH的度数．

查看试题解析
21. 已知关于 $x ， y$ 的方程组 ${\begin{array}{l} x + y = - 7 - k \\ x - y = 1 + 3 k \end{array}$ 的解 $x$ 为负数， $y$ 为非正数，求 $k$ 的取值范围

查看试题解析
22. 阅读下面的文字，解答问题：
大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来．于是小明用（ $\sqrt{2}$ -1）来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．

又例如：∵ $\sqrt{4}$ ＜ $\sqrt{7}$ ＜ $\sqrt{9}$ ，即∵2＜ $\sqrt{7}$ ＜3，

∴ $\sqrt{7}$ 的整数部分是2，小数部分为（ $\sqrt{7}$ -2）．

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是．

(2)、 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，则a＋b- $\sqrt{5}$ 的值；

(3)、已知： $10 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 ＜ y ＜ 1$ ，求 $x - y$ 的值．

查看试题解析
23. 为发展学生的核心素养，培养学生的综合能力，某学校计划开设四门选修课：乐器、舞蹈、绘画、书法，学校采取随机抽样的方法进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门）．对调查结果进行整理，绘制成如下两幅不完整的统计图．请结合图中所给信息解答下列问题：

(1)、本次调查的学生共有人，在扇形统计图中，m的值是．

(2)、分别求出参加调查的学生中选择绘画和书法的人数，并将条形统计图补充完整．

(3)、该校共有学生2000人，估计该校约有多少人选修乐器课程？

查看试题解析
24. 某商店销售 $A 、 B$ 两种玩具，这两种玩具的进价和售价如下表所示：

玩具

进价（元/件）

售价（元/件）

$A$

8

10

$B$

7

10

该商店计划购进这两种玩具若干件，共需2300元，全部销售后可获毛利润700元．

(1)、问该商店计划购进 $A 、 B$ 两种玩具各多少件？

(2)、通过市场调研，该商店决定在原计划的基础上，减少 $A$ 种玩具的购进数量，增加 $B$ 种玩具的购进数量．已知 $B$ 种玩具增加的数量是 $A$ 种玩具减少数量的1.5倍．如果用于购进这两种玩具的总资金不超过2550元，那么购进 $A$ 种玩具至多减少多少套．
（毛利益=（售价-进价）×销售量）

查看试题解析
25. 直线 $l_{1} ∥ l_{2}$ ，直线l₃、l₄分别与l₁、l₂交于点B、F和A、E，点D是直线l₃上一动点， $D C ∥ A B$ 交l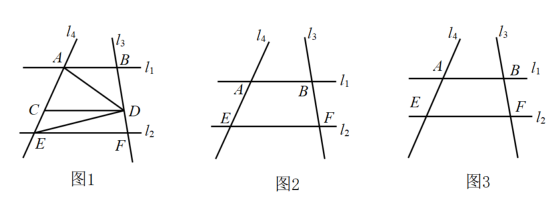₄于点C．

(1)、如图1，当点D在l₁、l₂两线之间运动时，试找出∠BAD、∠DEF、∠ADE之间的等量关系，并说明理由；

(2)、当点D在l₁、l₂两线外侧运动时，试探索∠BAD、∠DEF、∠ADE之间的等量关系（点D和B、F不重合），画出图形，直接写出结论．

查看试题解析

玩具	进价（元/件）	售价（元/件）
$A$	8	10
$B$	7	10