吉林省白城市洮北区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-05-12 类型：期末考试

进入出卷网下载

一、单选题

1. “天气预报”报道，今天的最低气温是20℃，最高气温是33℃，则今天气温t（℃）的取值范围是（）．

A、 $t < 33$ B、 $t > 20$ C、 $t = 20$ D、 $20 \leq t \leq 33$

查看试题解析
2. 下列生活现象中，属于平移的是（）

A、足球在草地上滚动 B、拉开抽屉 C、荡秋千 D、钟摆的摆动

查看试题解析
3. 下列方程中，是二元一次方程的是（）.

A、 $2 x + y = 0$ B、 $5 x y - y = 0$ C、 $3 x - 2 y = z$ D、 $\frac{1}{x} + y = 0$

查看试题解析
4. 在平面直角坐标系中，下列各点属于第三象限的是（）

A、（-1，5） B、（1，-5） C、（-1，-5） D、（1，5）

查看试题解析
5. 一元一次不等式组 ${\begin{array}{l} x > 3 \\ x > a \end{array}$ 的解集为 $x > 3$ ，那么a的值可能是（）

A、2 B、4 C、6 D、8

查看试题解析
6. 如图，测量运动员跳远成绩选取的是AB的长度，其依据是（）

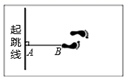A、两点确定一条直线 B、垂线段最短 C、两点之间线段最短 D、两点之间直线最短

查看试题解析

二、填空题

7. 9的算术平方根是．

查看试题解析
8. 若 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是关于x，y的方程 $x - a y = 3$ 的一个解，则a的值为．

查看试题解析
9. 调查神舟十四号飞船各设备的运行情况，宜采用调查的方式（用“全面”或“抽样”填空）．

查看试题解析
10. 已知点 $A (1 ， 2)$ ，过点A向y轴作垂线，垂足为M，则点M的坐标为．

查看试题解析
11. 如图， $A B ∥ C D$ ，点F在直线AB上， $E F ⊥ F G$ ．若 $∠ E F B = 150 °$ ，则 $∠ F G D$ 的大小为．

查看试题解析
12. 儿童节期间，欧亚超市想要打折促销一款玩具．该玩具成本是60元，定价为90元，要使利润率不低于5%，则该玩具最多可以打折．

查看试题解析
13. 命题“若 $- 3 a > - 3 b$ ，则 $a < b$ ”的逆命题是．

查看试题解析
14. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“美学”，如图， $\frac{B P}{A P} = \frac{\sqrt{5} - 1}{2}$ ，这个比值介于整数 $n$ 和 $n + 1$ 之间，则 $n$ 的值是．

查看试题解析

三、解答题

15. 计算： $\sqrt{16} - \sqrt[3]{8} + | 3 - 5 |$

查看试题解析
16. 解方程组 ${\begin{array}{l} x - y = 4 \\ 2 x + y = 5 \end{array}$ ．

查看试题解析
17. 解不等式： $\frac{x}{3} \geq 1 - \frac{x - 3}{6}$ ，并在数轴上表示解集．

查看试题解析
18. 如图，已知直线 $A B$ ， $C D$ ， $E F$ 相交于点 $O$ ， $A B ⊥ C D$ ， $∠ C O E = 53 °$ ，求 $∠ D O F$ 和 $∠ B O F$ 的度数．

查看试题解析
19. 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两（我国古代货币单位）；马三匹、牛五头，共价三十八两.问马、牛各价几何（马、牛单价各是多少两）？”

查看试题解析
20. 如图，在边长为1个单位的正方形网格中， $△ A B C$ 经过平移后得到 $△ A^{'} B^{'} C^{'}$ ，点B的对应点为点 $B^{'}$ ．

(1)、画出 $△ A^{'} B^{'} C^{'}$ ，线段AC扫过的图形的面积为；

(2)、在AB的右侧找到一个格点Q，使 $△ A B Q$ 的面积和 $△ A B C$ 的面积相等．

查看试题解析
21. 现有1元和5角的硬币共15枚，这些硬币的总币值小于9元．根据此信息，小强、小刚两名同学分别列出不完整的不等式如下：
小强： $x +$ ____ $< 9$ ，小刚： $0.5 x +$ ____ $< 9$ ．

(1)、小强同学所列的不等式中，x表示的是硬币的枚数：小刚同学所列的不等式中，x表示的是硬币的枚数；

(2)、在横线上补全小强、小刚两名同学所列的不等式；

(3)、任选其中一个不等式，求可能有几枚5角的硬币．

查看试题解析
22. 某校为创建书香校园，倡导读书风尚，开展了师生“大阅读”活动，并制订“大阅读”星级评选方案（以整数评分），每月评选一次．为了了解活动开展情况，某星期学校组织对全校八年级“大阅读”五星级评选工作进行抽样调查，随机抽取20名学生阅读的积分情况进行分析：
【收集数据】20名学生的“大阅读”积分如下（单位：分）：
32 43 34 35 15 46 48 24 45 10 25 40 60 42 55 30 47 28 37 42
【整理数据】
请你按如下表格分组整理、描述样本数据，并把下列表格补充完整．
积分/分
10≤x≤19
20≤x≤29
30≤x≤39
40≤x≤49
50≤x≤60
星级
红
橙
黄
绿
青
频数
2
3
5
m
n
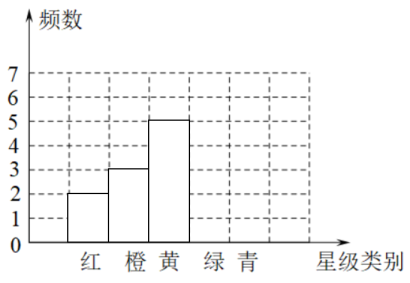
根据以上数据可制成不完整的频数分布直方图．

(1)、填空：m＝， n＝；

(2)、补全频数分布直方图；

(3)、【得出结论】
估计该校八年级600名学生中获得绿星级以上的人数．

(4)、已知该校八年级学生小艺的积分为a分，是绿星级；小贤的积分为b分，是青星级．如果俩人的积分均未出现在样本中，那么b-a的最大值是．

查看试题解析
23. 完成下面的推理过程：
如图，已知 $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 = ∠ B$ ，试说明：DE与BC平行．
解：∵ $∠ 1 + ∠ 2 = 180 °$ （已知）
又∵ $∠ 1 + ∠$   ▲   $= 180 °$ （邻补角意义）
∴ $∠$   ▲   $= ∠ D F E$ （同角的补角相等）
∴ $A B ∥$   ▲  （内错角相等，两直线平行）
∴ $∠ 3 = ∠$   ▲  （   ）
∵ $∠ 3 = ∠ B$ （已知）
∴ $∠ A D E = ∠$   ▲  （等量代换）
∴ $D E ∥$   ▲  （   ）

查看试题解析
24. 观察表格，回答问题：
a
…
0.0001
0.01
1
100
10000
…
$\sqrt{a}$
…
0.01
x
1
y
100
…

(1)、表格中 $x =$ ， $y =$ ；

(2)、从表格中探究a与 $\sqrt{a}$ 数位的规律，并利用这个规律解决下面两个问题：
①已知 $\sqrt{10} \approx 3.16$ ，则 $\sqrt{1000} ≈$ ▲ ；
②已知 $\sqrt{m} = 8.973$ ，若 $\sqrt{b} = 897.3$ ，用含m的代数式表示b，则 $b =$ ▲ ；

(3)、试比较 $\sqrt{a}$ 与a的大小．
当时， $\sqrt{a} > a$ ；当时， $\sqrt{a} = a$ ；当时， $\sqrt{a} < a$ ．

查看试题解析
25. 如图，已知PM $∥$ AN，且∠A＝40°，点C是射线AN上一动点（不与点A重合），PB，PD分别平分∠APC和∠MPC，交射线AN于点B，D．

(1)、求∠BPD的度数；

(2)、当点C运动到使∠PBA＝∠APD时，求∠APB的度数；

(3)、在点C运动过程中，∠PCA与∠PDA之间是否存在一定的数量关系？若存在，请写出它们之间的数量关系，并说明理由；若不存在，请举出反例．

查看试题解析
26. 为降低空气污染，漯河市公交公司决定全部更换节能环保的燃气公交车，计划购买A型和B型两种公交车共10辆，其中每台的价格，年载客量如表：

A型
B型
价格（万元/辆）
a
b
年均载客量（万人/年/辆）
60
100
若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元.

(1)、求a、b的值：

(2)、如果该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你利用方程组或不等式组设计一个总费用最少的方案，并说明总费用最少的理由.

查看试题解析

积分/分	10≤x≤19	20≤x≤29	30≤x≤39	40≤x≤49	50≤x≤60
星级	红	橙	黄	绿	青
频数	2	3	5	m	n

	A型	B型
价格（万元/辆）	a	b
年均载客量（万人/年/辆）	60	100

a	…	0.0001	0.01	1	100	10000	…
$\sqrt{a}$	…	0.01	x	1	y	100	…