广东省江门市蓬江区2021-2022学年七年级下学期期末调研考试数学试题

试卷更新日期：2023-05-12 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（）

A、 $- \frac{1}{2}$ B、 $| - 2 |$ C、 $\sqrt{9}$ D、 $π$

查看试题解析
2. 在平面直角坐标系中，点 $P (\sqrt{3} ， - 3)$ 位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 空气是由多种气体混合而成的，为了简明扼要的介绍空气的组成情况，较好的描述数据，最适合使用的统计图是（）

A、扇形图 B、条形图 C、折线图 D、直方图

查看试题解析
4. 下列命题中，是假命题的是（）

A、直角的补角是直角 B、内错角相等，两直线平行 C、一条直线有且只有一条垂线 D、垂线段最短

查看试题解析
5. 若 $h = \sqrt{11} - 1$ ，则估计h的值所在的范围是（）

A、 $3 < h < 4$ B、 $2 < h < 3$ C、 $1 < h < 2$ D、 $0 < h < 1$

查看试题解析
6. 一组数据中的最小值是31，最大值是113，分析这组数据时，若取组距为10，则组数为（）

A、7 B、8 C、9 D、10

查看试题解析
7. 如图，长方形ABCD的长AB为8，宽AD为6，将这个长方形向上平移3个单位，再向左平移2个单位，得到长方形EFGH，则阴影部分的面积为（）

A、30 B、32 C、36 D、40

查看试题解析
8. 实数a、b在数轴上的对应点的位置如图所示，下列结论正确的是（）

A、 $a > b$ B、 $a + b > 0$ C、 $| a | < | b |$ D、 $- a > b$

查看试题解析
9. 若点 $P (x ， y)$ 在第一象限内，且点P到两坐标轴的距离相等，并满足方程组 ${\begin{array}{l} 3 x - y = 4 \\ a x + y = 8 \end{array}$ ，则a的值为（）

A、3 B、4 C、5 D、6

查看试题解析
10. 已知关于x的不等式组 ${\begin{array}{l} 3 x - m > 0 \\ x - 1 \leq 5 \end{array}$ 有四个整数解，则m的取值范围是（）

A、 $2 \leq m < 3$ B、 $6 \leq m < 9$ C、 $3 < m \leq 6$ D、 $5 < m ≤ 7$

查看试题解析

二、填空题

11. $\sqrt{4}$ 的平方根是．

查看试题解析
12. 已知方程 $3 x - y = 4$ ，改写成用含x的式子表示y的形式．

查看试题解析
13. 如图，将一块三角尺的直角顶点放在直尺的一边上，当 $∠ 1 = 23 °$ 时， $∠ 2$ 的度数为．

查看试题解析
14. 若不等式 $(\sqrt{2} - a) x > \sqrt{2} - a$ 的解集是 $x < 1$ ，则a的取值范围是．

查看试题解析
15. 若 $\sqrt[3]{15.3} \approx 2.4825$ ， $\sqrt[3]{x} \approx 24.825$ ，那么 $x =$ ．

查看试题解析
16. 古希腊数学家把数1，3，6，10，15，21，……叫做三角数，它有一定的规律性，若把第一个三角数记为 $a_{1}$ ，第二个三角数记为 $a_{2}$ ， ……．第n个三角数记为 $a_{n}$ ，计算 $a_{99} + a_{100} =$ ．

查看试题解析
17. 如图，已知 $A B ∥ C D$ ，点 $M$ ， $N$ 分别在直线 $A B$ 、 $C D$ 上， $∠ M E N = 90 °$ ， $∠ C N E = ∠ E N F$ ，则 $∠ α$ 与 $∠ β$ 的数量关系．

查看试题解析

三、解答题

18. 计算： $\sqrt{2^{2}} + \sqrt[3]{- 64} + | 1 - \sqrt{2} | - \sqrt{2} (\sqrt{2} - 3)$

查看试题解析
19. 解方程组： ${\begin{array}{l} 2 x + 3 y = 1 \\ 5 x - 6 y = 16 \end{array}$

查看试题解析
20. 解不等式组： ${\begin{array}{l} 3 x - 5 < x \\ \frac{x + 5}{3} - x \leq 1 \end{array}$ ，并写出它的所有整数解．

查看试题解析
21. 如图，三角形 $A B C$ 中任意一点 $P (x_{0} ， y_{0})$ 经平移后对应点为 $P_{1} (x_{0} - 2 ， y_{0} - 3)$ ，将三角形 $A B C$ 作同样的平移得到三角形 $A_{1} B_{1} C_{1}$ ．

(1)、画出三角形 $A_{1} B_{1} C_{1}$ ；

(2)、请直接写出 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标；

(3)、求三角形 $A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
22. 新冠肺炎疫情期间，某市防控指挥部想了解自2月至4月各学校教职工参与志愿服务的情况．在全市各学校随机调查了部分参与志愿服务的教职工，对他们的志愿服务时间进行统计，整理并绘制成两幅不完整的统计图表，根据两幅统计图表中的信息回答问题：

志愿服务时间（小时）
频数
A
$0 < x \leq 30$
2
B
$30 < x \leq 60$
b
C
$60 < x \leq 90$
12
D
$90 < x \leq 120$
18

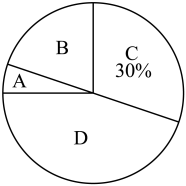(1)、本次被抽取的教职工共有名；

(2)、表中 $b =$ ，扇形统计图中“A”部分所占百分比为；

(3)、扇形统计图中，“D”所对应的扇形圆心角的度数为；

(4)、若该市共有20000名教职工参与志愿服务，请估算志愿服务时间多于60小时的教职工有多少人？

查看试题解析
23. 如图，已知点 $A$ 、 $D$ 在直线 $E F$ 上， $∠ 1 + ∠ 2 = 180 °$ ， $D B$ 平分 $∠ A D C$ ， $A D ∥ B C$ ．

(1)、求证： $A B ∥ D C$ ；

(2)、若 $∠ D A B = 128 °$ ，求 $∠ D B C$ 的度数．

查看试题解析
24. 某商店准备购进甲、乙两种品牌纪念品，若购进甲种纪念品 $40$ 个，乙种纪念品 $25$ 个，需要 $1350$ 元；若购进甲种纪念品 $20$ 个，乙种纪念品 $30$ 个，需要 $1200$ 元．

(1)、求购进甲、乙两种纪念品每个各需多少元？

(2)、若该商店刚好用了 $3000$ 元购进这两种纪念品，考虑顾客需求，要求购进甲种纪念品的数量不少于乙种纪念品数量的 $3$ 倍，且乙种纪念品数量大于 $38$ 个，那么该商店有几种进货方案？

(3)、若该商店销售每个甲种纪念品可获利润 $5$ 元，销售每个乙种纪念品可获利润 $6$ 元，在第（2）问的进货方案中，哪一种方案获利最大？最大利润是多少？

查看试题解析
25. 在平面直角坐标系中，点 $O$ 是坐标原点，点 $A$ 的坐标是 $(a ， - a)$ ，点 $B$ 的坐标是 $(b ， c)$ ，且 $a$ ， $b$ ， $c$ 满足 ${\begin{array}{l} 3 a - b + 2 c = 6 \\ a - 2 b - c = - 3 \end{array}$ ．

(1)、若 $a$ 为不等式 $2 x + 8 \leq 0$ 的最大整数解，判断点 $A$ 在第几象限，说明理由；

(2)、求点 $B$ 的坐标；

(3)、若有两个动点 $M (k - 1 ， k)$ 、 $N (- 3 h + 10 ， h)$ ，请探索是否存在以两个动点 $M$ 、 $N$ 为端点的线段 $M N ∥ A B$ ，且 $M N = A B$ ，若存在，求 $M$ 、 $N$ 两点的坐标；若不存在，请说明理由．

查看试题解析

	志愿服务时间（小时）	频数
A	$0 < x \leq 30$	2
B	$30 < x \leq 60$	b
C	$60 < x \leq 90$	12
D	$90 < x \leq 120$	18