浙江省宁波市江北区2023年中考一模数学试题

试卷更新日期：2023-05-12 类型：中考模拟

进入出卷网下载

一、选择题（每小题4分，共40分）

1. 在-2，-1，0，2这四个数中，最小的数是（）

A、-2 B、-1 C、0 D、2

查看试题解析
2. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{3} \div a = a^{3}$ C、 ${(a^{5})}^{2} = a^{7}$ D、 $a^{3} + a^{3} = 2 a^{3}$

查看试题解析
3. “宁波地铁”发文称，2023年2月13日至6月30日，每天晚上8点后及法定节假日全天，宁波地铁1—5号线全线网皆可免费乘车，免费时段无需购票、刷卡、扫码，可直接进站乘车.2月17日，宁波地铁限时段免费后的首个周五，地铁客流量达到约107.6万人次．数107.6万用科学记数法表示为（）

A、 $1.076 \times 10^{5}$ B、 $10.76 \times 10^{5}$ C、 $1.076 \times 10^{6}$ D、 $0.1076 \times 10^{6}$

查看试题解析
4. 如图是某品牌的多功能笔筒，其俯视图为（）

A、 B、 C、 D、

查看试题解析
5. 能说明命题“对于任意实数 $x$ ， $x^{2} > 0$ ”是假命题的一个反例可以是（）

A、 $x = \sqrt{3}$ B、 $x = 1$ C、 $x = 0$ D、 $x = - 1$

查看试题解析
6. 某鞋店对某款女鞋一周的销售情况进行统计，结果如下：

尺码

35

36

37

38

39

40

销售量（双）

6

18

33

12

2

1

根据上表信息，该店主决定下周多进一些37码的鞋子，影响店主进货决策的统计量是（）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
7. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 36 °$ ．以点 $B$ 为圆心，适当长为半径作圆弧，交 $A B$ 于点 $M$ ，交 $B C$ 于点 $N$ ．接着分别以点 $M$ ， $N$ 为圆心，大于 $\frac{1}{2} M N$ 长为半径作圆弧，两弧交于点 $H$ ．作射线 $B H$ ，交 $A C$ 于点 $D$ ．再以点 $D$ 为圆心， $D C$ 长为半径作圆弧，交 $B C$ 于点 $E$ ，连结 $D E$ ．则下列说法错误的是（）

A、 $A D = B D$ B、 $∠ B D C = ∠ B C D$ C、 $A D = \sqrt{3} B E$ D、 $△ B E D ∽ △ B D A$

查看试题解析
8. 《张丘建算经》是中国古代数学著作，其中提出了许多数学问题，比如：“今有甲乙怀钱各不知其数，甲得乙十钱，多乙余钱五倍；乙得甲十钱，适等；问甲乙怀钱各几何？”可以理解为：甲乙两人各有一些钱，若乙给甲10元，则甲的钱比乙多5倍；若甲给乙10元，则两人的钱一样多．不妨设甲原有钱 $x$ 元，乙原有钱 $y$ 元，则可列方程组为（）

A、 ${\begin{cases} x + 10 = 5 (y - 10) \\ x - 10 = y + 10 \end{cases}$ B、 ${\begin{cases} x + 10 = 6 (y - 10) \\ x - 10 = y + 10 \end{cases}$ C、 ${\begin{cases} x - 10 = 5 (y + 10) \\ x + 10 = y - 10 \end{cases}$ D、 ${\begin{cases} x - 10 = 6 (y + 10) \\ x + 10 = y - 10 \end{cases}$

查看试题解析
9. 如图是由4个全等的大正方形和5个全等的小正方形组成的图形．若要求线段 $M N$ 的长度，只需要知道顶点 $P$ 与正方形 $A B D C$ 某个顶点之间的距离即可，这个点是（）

A、点 $A$ B、点 $B$ C、点 $C$ D、点 $D$

查看试题解析
10. 已知抛物线 $y = {(x - b)}^{2} + c$ 经过 $A (1 - n ， y_{1})$ ， $B (n ， y_{2})$ ， $C (n + 3 ， y_{3})$ 三点， $y_{1} = y_{3}$ ．当 $1 - n \leq x \leq n$ 时，二次函数的最大值与最小值的差为16，则 $n$ 的值为（）

A、-5 B、3 C、 $\frac{19}{6}$ D、4

查看试题解析

二、填空题（每小题5分，共30分）

11. $\sqrt{4}$ = ．

查看试题解析
12. 因式分解： $b^{2} - 9 =$ ．

查看试题解析
13. 如图，小江，小北周末都在荪湖公园踏春．小江在三岔路口 $A$ 处，随意选择一条路准备出园，小江与在其中一条路上的 $B$ 景点处游玩的小北邂逅的概率是．

查看试题解析
14. 如图，在 $△ A B C$ 中，分别以 $A B$ ， $A C$ 为斜边在同侧作两个等腰直角 $△ A D B$ 与 $△ A E C$ ，若点 $D$ 是 $△ A E C$ 的重心，则 $\tan ∠ B A C =$ ．

查看试题解析
15. 如图1，在 $▱ A B C D$ 中， $∠ A = 60 °$ ，动点 $E$ ， $F$ 从点 $A$ 同时出发，分别沿 $A \to B \to C$ 和 $A \to D \to C$ 的方向都以每秒1个单位长度的速度运动，到达点 $C$ 后停止运动．设运动时间为 $t (s)$ ， $△ A E F$ 的面积为 $y$ ， $y$ 与 $t$ 的大致函数关系如图2所示．则当 $y = \frac{\sqrt{3}}{4}$ 时， $t$ 的值为．

查看试题解析
16. 如图，菱形 $A B C O$ 的顶点 $A$ 与对角线交点 $D$ 都在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上，对角线 $A C$ 交 $y$ 轴于点 $E$ ， $C E = 2 D E$ ，且 $△ A D B$ 的面积为15，则 $k =$ ；延长 $B A$ 交 $x$ 轴于点 $F$ ，则点 $F$ 的坐标为．

查看试题解析

三、解答题（本大题有8小题，共80分）

17.

(1)、计算： ${(a + 1)}^{2} - a (a + 1)$ ．

(2)、解不等式组： ${\begin{cases} 3 x - 5 < 1 \\ 2 x + 1 \geq x \end{cases}$ ．

查看试题解析
18. 如图，下列3×4网格图均由12个相同的小正方形组成，每个网格图中有2个小正方形已涂上阴影，请在余下的空白小正方形中，分别按下列要求选取两个涂上阴影：

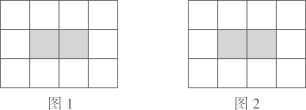(1)、使得4个阴影小正方形组成的图形是轴对称图形，但不是中心对称图形．

(2)、使得4个阴影小正方形组成的图形是中心对称图形，但不是轴对称图形．
请将以上两个小题依次作答在图1，图2中，均只需画出符合条件的一种情形即可．

查看试题解析
19. 今天，4月20日恰逢24节气中的谷雨．播谷降雨，雨生百谷，这也是春季的最后一个节气．在古代，各地都有着不同的习俗活动来迎接与庆祝，有赏花、品茗、走谷雨（踏春）、洗桃花水（沐浴）、吃椿（香椿）等．为了了解学生最感兴趣的一项活动的人数分布情况，学校从全校学生中随机抽取100名学生进行问卷调查，并绘制了如下两幅统计图．

(1)、请计算最感兴趣活动为“洗桃花水（沐浴）”的学生总人数，并补全条形统计图．

(2)、请计算最感兴趣活动为“走谷雨（踏春）”的女生人数．

(3)、男生最感兴趣活动中“洗桃花水（沐浴）”和“吃椿（香椿）”的人数相同吗？为什么？

查看试题解析
20. 如图，一次函数 $y = a x + b (a \neq 0)$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于 $A (m ， 2)$ ， $B (1 ， 6)$ 两点．

(1)、求反比例函数和一次函数的函数表达式；

(2)、根据图象直接写出满足当 $a x + b > \frac{k}{x}$ 时， $x$ 的取值范围．

查看试题解析
21. 桑梯——登以採桑，它是我国古代劳动人民发明的一种采桑工具．图1是明朝科学家徐光启在《农政全书》中用图画描绘的桑梯，其示意图如图2所示，已知 $A B = A C = 1.6$ 米， $A D = 1.2$ 米，设 $∠ B A C = α$ ，为保证安全， $α$ 的调整范围是 $30 ° \leq α \leq 90 °$ ．

(1)、当 $α = 60 °$ 时，若人站在 $A D$ 的中点 $E$ 处，求此人离地面（ $B C$ ）的高度．

(2)、在安全使用范围下，求桑梯顶端 $D$ 到地面 $B C$ 的距离范围．
（参考数据： $\sin 75 ° \approx 0.97$ ， $\cos 75 ° \approx 0.26$ ， $\tan 75 ° \approx 3.73$ ， $\sqrt{3} \approx 1.73$ ， $\sqrt{2} \approx 1.41$ ，精确到0.1米）

查看试题解析
22. 乌馒头是江北慈城地方特色点心，用麦粉发酵，再掺以白糖黄糖，蒸制而成．因其用黄糖，颜色暗黄，所以称之谓“乌馒头”．某商店销售乌馒头，通过分析销售情况发现，乌馒头的日销售量 $y$ （盒）是销售单价 $x$ （元/盒）的一次函数，销售单价、日销售量的部分对应值如下表，已知销售单价不低于成本价且不高于20元，每天销售乌馒头的固定损耗为20元，且销售单价为18元/盒时，日销售纯利润为1180元．

销售单价 $x$ （元/盒）

15

13

日销售量 $y$ （盒）

500

700

(1)、求乌馒头的日销售量 $y$ （盒）与销售单价 $x$ （元/盒）的函数表达式；

(2)、“端午乌馒重阳粽”是慈城的习俗．端午节期间，商店决定采用降价促销的方式回馈顾客．在顾客获得最大实惠的前提下，当乌馒头每盒降价多少元时，商店日销售纯利润为1480元？

(3)、当销售单价定为多少时，日销售纯利润最大，并求此日销售最大纯利润．

查看试题解析
23. 如图

(1)、【基础巩固】
如图1，在 $△ A B C$ 中， $D$ 是 $B C$ 的中点， $E$ 是 $A C$ 的一个三等分点，且 $A E = \frac{1}{3} A C$ ．连结 $A D$ ， $B E$ 交于点 $G$ ，则 $A G ： G D =$ ； $B G ： G E =$ ．

(2)、【尝试应用】
如图2，在 $△ A B C$ 中， $E$ 为 $A C$ 上一点， $A B = A E$ ， $∠ B A D = ∠ C$ ，若 $A D ⊥ B E$ ， $C E = 1$ ， $A E = 3$ ，求 $A D$ 的长．

(3)、【拓展提高】
如图3，在 $▱ A B C D$ 中， $F$ 为 $B C$ 上一点， $E$ 为 $C D$ 中点， $B E$ 与 $A C$ ， $A F$ 分别交于点 $G$ ， $M$ ，若 $∠ B A F = ∠ D A C$ ， $A B = A G$ ， $B F = 2$ ， $B M = 2 M G$ ，求 $A M$ 的长．

查看试题解析
24. 如图，等腰 $△ A B C$ 内接于 $⊙ O$ ，其中 $A B = B C$ ，点 $D$ 在 $\overset{⌢}{A B}$ 上运动， $\overset{⌢}{A D} = \overset{⌢}{B E}$ ， $D E$ 分别交 $A B$ 、 $B C$ 于点 $P$ 、 $Q$ ， $C D$ 交 $A B$ 于点 $M$ ．

(1)、求证： $\overset{⌢}{B D} = \overset{⌢}{C E}$ ．

(2)、连结 $A E$ ，当 $A E$ 为 $⊙ O$ 的直径时，
①求证： $C D ⊥ A B$ ．

②连结 $Q M$ ，若 $M Q ∥ A E$ ，求 $\tan ∠ E A C$ 的值．

③连结 $C E$ ，设 $\frac{P Q}{P D} = x$ ， $\frac{C E}{P M} = y$ ，请直接写出 $y$ 关于 $x$ 的函数表达式．

查看试题解析

销售单价 $x$ （元/盒）	15	13
日销售量 $y$ （盒）	500	700

尺码	35	36	37	38	39	40
销售量（双）	6	18	33	12	2	1