浙江省宁波市镇海区2023年中考一模数学试题
试卷更新日期:2023-05-12 类型:中考模拟
一、选择题(每小题4分,共40分)
-
1. 在-3,-1,0,2这四个数中,最小的数是( )A、0 B、-1 C、-3 D、2. 计算-a3÷a的结果是( )A、-3 B、-2a C、a2 D、-a23. 2023年3月12日是第45个中国植树节,广大市民以多种方式参与到植树、护绿中来.据某市公园城市建设管理局初步统计,今年截至3月12日,全市约76.4万人参与活动,义务植树268.4万株.数据268.4万用科学记数法可表示为( )A、2.684×102 B、268.4×104 C、2.684×105 D、2.684×1064. 如图所示的钢块零件的左视图为( )
 A、
A、 B、
B、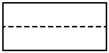 C、
C、 D、
D、 5. 甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是S甲2=0.12,S乙2=0.25,S丙2=0.35,S丁2=0.46,在本次射击测试中,这四个人成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁6. 要使分式有意义,则x应满足的条件是( )A、x≠-1 B、x≠1 C、x>-1 D、x>17. 如图,直线m∥n,直角三角尺ABC的直角顶点C在这两直线之间,两直角边与两直线相交所形成的锐角分别为α,β.若α=35°,则β的值为( )
5. 甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是S甲2=0.12,S乙2=0.25,S丙2=0.35,S丁2=0.46,在本次射击测试中,这四个人成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁6. 要使分式有意义,则x应满足的条件是( )A、x≠-1 B、x≠1 C、x>-1 D、x>17. 如图,直线m∥n,直角三角尺ABC的直角顶点C在这两直线之间,两直角边与两直线相交所形成的锐角分别为α,β.若α=35°,则β的值为( )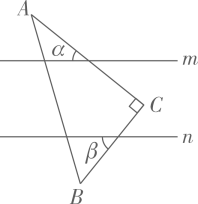 A、55° B、35° C、45° D、50°8. 《孙子算经》是南北朝时期重要的数学专著,包含“鸡兔同笼”等许多有趣的数学问题.如:“今有木,不知长短,引绳度之,余绳四尺五寸:屈绳量之,不足一尺.木长几何?”大意是:“用一根绳量一根木,绳剩余4.5尺;将绳对折再量木,木剩余1尺.问木长多少?”设木长x尺,绳长y尺,则依题意可列方程组( )A、 B、 C、 D、9. 若把二次函数y=ax2+bx+c(a≠0)的图象向左平移4个单位或向右平移1个单位后都会经过原点,此二次函数图象的对称轴是( )A、直线x=-2.5 B、直线x=2.5 C、直线x=-1.5 D、直线x=1.510. 如图,以直角三角形的各边为边向外作正方形,再把较小的两个正方形放置在最大的正方形内,若知道图中阴影部分的面积,则一定能求出哪个图形的面积( )
A、55° B、35° C、45° D、50°8. 《孙子算经》是南北朝时期重要的数学专著,包含“鸡兔同笼”等许多有趣的数学问题.如:“今有木,不知长短,引绳度之,余绳四尺五寸:屈绳量之,不足一尺.木长几何?”大意是:“用一根绳量一根木,绳剩余4.5尺;将绳对折再量木,木剩余1尺.问木长多少?”设木长x尺,绳长y尺,则依题意可列方程组( )A、 B、 C、 D、9. 若把二次函数y=ax2+bx+c(a≠0)的图象向左平移4个单位或向右平移1个单位后都会经过原点,此二次函数图象的对称轴是( )A、直线x=-2.5 B、直线x=2.5 C、直线x=-1.5 D、直线x=1.510. 如图,以直角三角形的各边为边向外作正方形,再把较小的两个正方形放置在最大的正方形内,若知道图中阴影部分的面积,则一定能求出哪个图形的面积( )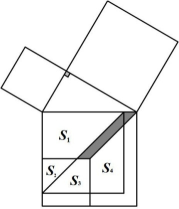 A、S1 B、S2 C、S3 D、S4
A、S1 B、S2 C、S3 D、S4二、填空题(每小题5分,共30分)
-
11. |-2023|= .12. 把多项式2x2-2分解因式的结果是 .13. 在一个不透明的布袋中装有4个白球和6个黄球,它们除了颜色不同外,其余均相同,若从中随机摸出一个球,则摸到白球的概率是 .14. 有一个圆心角为120°,半径长为9cm的扇形,若将其围成一圆锥侧面,那么这个圆锥的底面圆的半径是cm.15. 在平面直角坐标系中,对于任意一个不在坐标轴上的点P(x,y),我们把点P′(x+y,x-y)称为点P的“和差点”.若直线y=-2x+1上有两个点A和B,它们的和差点A′和B′均在反比例函数上,则△OAB的面积为 .16. 如图,点E是正方形ABCD的边BC上一点,FG垂直平分AE且分别交AB,AE,BD,CD于点F,H,I,G.若FH=2,IG=6,则HI的长度为 , sin∠FIB的值为 .

三、解答题(本大题有8小题,共80分)
-
17.(1)、计算:(2)、解不等式组:18. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
 (1)、如图1,△ABC的外接圆的圆心是点O,D是弧BC的中点,画一条弦AE把△ABC分成面积相等的两部分;(2)、如图2,△ABC是⊙O的内接三角形,且AB=AC,过点B画弦BD∥AO;(3)、如图3,△ABC是⊙O的内接三角形,弦AD∥BC,画∠BAC的平分线交BC于点E.19. 某学校为了增强学生体质,决定开设以下体育课外活动项目:篮球、羽毛球、乒乓球、踢毽子、跳绳.为了解学生对这5项体育活动的喜欢程度,随机抽取了部分学生进行调查(每人只选一项),并将统计数据绘制成两幅不完整的统计图:
(1)、如图1,△ABC的外接圆的圆心是点O,D是弧BC的中点,画一条弦AE把△ABC分成面积相等的两部分;(2)、如图2,△ABC是⊙O的内接三角形,且AB=AC,过点B画弦BD∥AO;(3)、如图3,△ABC是⊙O的内接三角形,弦AD∥BC,画∠BAC的平分线交BC于点E.19. 某学校为了增强学生体质,决定开设以下体育课外活动项目:篮球、羽毛球、乒乓球、踢毽子、跳绳.为了解学生对这5项体育活动的喜欢程度,随机抽取了部分学生进行调查(每人只选一项),并将统计数据绘制成两幅不完整的统计图: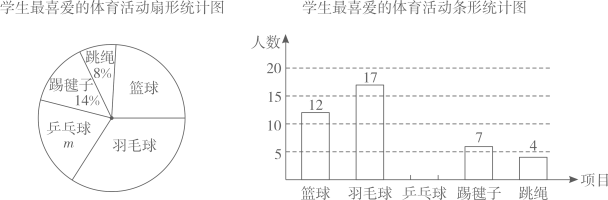
根据以上信息,解答下列问题:
(1)、这次抽样调查的样本容量是;(2)、将条形统计图补充完整,并求出m=▲ _%;(3)、羽毛球所对应扇形的圆心角的大小是多少度?(4)、若全校有1200名学生,估计全校喜欢篮球和乒乓球的共有多少名学生?20. 如图,Rt△ABO的顶点A是双曲线与直线y2=-x-(k+1)在第二象限的交点,AB⊥x轴于点B, (1)、求k的值;(2)、求A、C两点的坐标;(3)、根据图像直接写出y1>y2时x的取值范围.21. 如图所示为汽车内常备的一种菱形千斤顶的原理图,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变∠ADC的大小(菱形的边长不变),从而改变千斤顶的高度(即A、C之间的距离).经测量,∠ADC可在20°和160°之间发生变化,(包含20°和160°),AD=40cm.
(1)、求k的值;(2)、求A、C两点的坐标;(3)、根据图像直接写出y1>y2时x的取值范围.21. 如图所示为汽车内常备的一种菱形千斤顶的原理图,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变∠ADC的大小(菱形的边长不变),从而改变千斤顶的高度(即A、C之间的距离).经测量,∠ADC可在20°和160°之间发生变化,(包含20°和160°),AD=40cm. (1)、当∠ADC=120°时,求此时BD的长;(2)、当∠ADC从20°变为160°时,这个千斤顶升高了多少cm?(sin80°=0.98,cos80°=0.17,tan80°=5.67)22. 某景区有两个景点需购票游览,售票处出示的三种购票方式如下:
(1)、当∠ADC=120°时,求此时BD的长;(2)、当∠ADC从20°变为160°时,这个千斤顶升高了多少cm?(sin80°=0.98,cos80°=0.17,tan80°=5.67)22. 某景区有两个景点需购票游览,售票处出示的三种购票方式如下:方式1:只购买景点A,30元/人;
方式2:只购买景点B,50元/人;
方式3:景点A和B联票,70元/人.
预测,四月份选择这三种购票方式的人数分别有2万、1万和1万.为增加收入,对门票价格进行调整,发现当方式1和2的门票价格不变时,方式3的联票价格每下降1元,将有原计划只购买A门票的400人和原计划只购买B门票的600人改为购买联票.
(1)、若联票价格下降5元,则购买方式1门票的人数有万人,购买方式2门票的人数有万人,购买方式3门票的人数有万人;并计算门票总收入有多少万元?(2)、当联票价格下降x(元)时,请求出四月份的门票总收入w(万元)与x(元)之间的函数关系式,并求出联票价格为多少元时,四月份的门票总收入最大?最大值是多少万元?23. 如图,AD是锐角△ABC中BC边上的高,将△ABD沿AB所在的直线翻折得到△ABE,将△ADC沿AC所在的直线翻折得到△AFC,延长EB,FC相交于点P. (1)、如图1,若∠BAC=45°,求证:四边形AEPF为正方形;(2)、如图2,若∠BAC=55°,当△PBC是等腰三角形时,求∠BAD的度数;(3)、如图3,连结EF,分别交AB,AC于点G、H,连结BH交AD于点M,若∠BAC=60°,
(1)、如图1,若∠BAC=45°,求证:四边形AEPF为正方形;(2)、如图2,若∠BAC=55°,当△PBC是等腰三角形时,求∠BAD的度数;(3)、如图3,连结EF,分别交AB,AC于点G、H,连结BH交AD于点M,若∠BAC=60°,①求∠PEF=▲ 度;
②若AB=10,CH=1,求△ABM的面积.
24.(1)、【教材呈现】以下是浙教版八年级下册数学教材第85页的部分内容.先观察图4-17,直线l1∥l2,点A,B在直线l2上,点C1 , C2 , C3 , C4在直线l1上.△ABC1 , △ABC2 , △ABC3 , △ABC4这些三角形的面积有怎样的关系?请说明理由。
 (2)、【基础巩固】如图1,正方形ABCD内接于⊙O,直径MN∥AD,求阴影面积与圆面积的比值;(3)、【尝试应用】如图2,在半径为5的⊙O中,BD=CD,∠ACO=2∠BDO,cos∠BOC=x,用含x的代数式表示S△ABC;(4)、【拓展提高】如图3,AB是⊙O的直径,点P是OB上一点,过点P作弦CD⊥AB于点P,点F是⊙O上的点,且满足CF=CB,连接BF交CD于点E,若BF=8EP,S△CEF=10 ,求⊙O的半径.
(2)、【基础巩固】如图1,正方形ABCD内接于⊙O,直径MN∥AD,求阴影面积与圆面积的比值;(3)、【尝试应用】如图2,在半径为5的⊙O中,BD=CD,∠ACO=2∠BDO,cos∠BOC=x,用含x的代数式表示S△ABC;(4)、【拓展提高】如图3,AB是⊙O的直径,点P是OB上一点,过点P作弦CD⊥AB于点P,点F是⊙O上的点,且满足CF=CB,连接BF交CD于点E,若BF=8EP,S△CEF=10 ,求⊙O的半径.